Тема урока: Свойства и графики тригонометрических функций (3 урок) в 10 классе
Цели: 1. Обучающая . Отработать умения и навыки построения графиков тригонометрических
функций и использование свойств для решения упражнений, построение графика тригонометрических функций с помощью простейших преобразований y = к f ( аx- b) + d, показать, что колебания повсюду сопровождают нас;
показать, что знание свойств тригонометрических функций важно для изучения положительного и отрицательного воздействия колебаний.
Научить строить графики гармонических колебаний .Показать межпредметную связь математики и физики.
преобразование суммы и разности тригонометрических функций в произведение.
преобразование произведения тригонометрических функций в сумму и разность.
2. Развивающая. Развивать умения и навыки построения графика, рассматривая свойства функций.
умение анализировать, обобщать и выделять главное, имеющиеся знания в
новую ситуацию.
3. Воспитывающая. Воспитывать у учащихся трудолюбие, дисциплинированность,
добросовестное отношение к учебе.
Тип урока: комплексное применение знаний и способов деятельности
1.Алгоритмический метод и классификация изученного.
2.Частично- поисковый метод.
3. Решение задач тренировочного характера.
Оборудование урока: Учебник алгебры 10 кл. А.Е. Абылкасымова, «Мектеп», доска,
рабочая тетрадь, инструменты, таблицы формул.
Нет ни одной области математики, которая когда-нибудь не окажется применимой к явлениям действительного мира. (Н.И. Лобачевский)
Ход урока:
| Этапы Урока | Содержание урока |
| 1 | Организационный момент. Приветствие, сообщение темы и задач урока. Нет ни |
| 2 | Этап проверки домашнего задания.
|
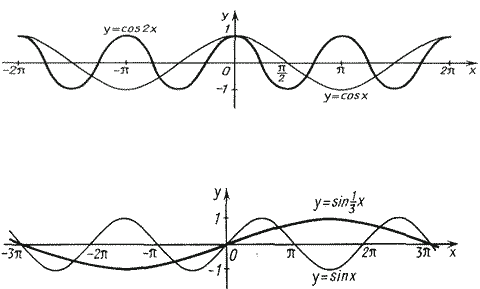
| 3 | Актуализация .Устный опрос правил и определений: 1. Свойства и графики тригонометрических функций: четность, периодичность, возрастание и убывание функции, экстремумы, обратные функции. 2. Построение графика тригонометрических функций с помощью простейших преобразований y = к f ( аx- b) + d. Построить график y = 3 sin (2x + 2π/3) 3. Преобразование произведения тригонометрических функций в сумму и разность. 4. преобразование суммы и разности тригонометрических функций в произведение.
|
|
4 | Мотивация . Нет ни одной области математики, которая когда-нибудь не окажется применимой к явлениям действительного мира. Н.И. Лобачевский. Зачем человеку нужно в жизни знание свойств функций и умение читать графики? Любые периодически повторяющиеся движения называются КОЛЕБАНИЯМИ Практика изучения колебаний показала полезную и вредную роль. Каждому специалисту необходимо владеть теорией колебательных процессов. Теория колебаний- это область науки, связанная с математикой и физикой. Гармонические колебания Механические колебания Вибрация. Вредные воздействия вибрации Ультразвук Инфразвук звук Электромагнитные колебания (применяются для радио, телевидения, связи с космическими объектами) Для чего нужно измерять колебания? Измерения выявляют опасные состояния модели.
Вывод : Колебания происходят по законам синусов и косинусов |
| 5 | Применение. Формирование умений и навыков. Работа в группах 1.(составление кластера) по колебаниям. 2. Задание 1 Какие преобразования нужно выполнить, чтобы построить график данной функции? 1) f(x) = 0,5 cos x 2) f(x) = 3 + sin x 3) f(x) = sin (x - П/4) 4)f(x) = 2cos (x /2 + П/3 ) Задание 2. Задание 2 .построение графика функции у = f (x) + b, где b - постоянное число Например: а) y = sin x + 2; а) y = sin x - 5; Задание 3. Проявите смекалку Творческое задание. Какое из свойств тригонометрических функций вы видите в каждой из этих пословиц? Пословицы и поговорки Декабрь год кончает, а зиму начинает. Убывание возрастание функции, точка минимума У дороги конца нет. Область определения синуса Повторенье - мать ученья. Период Не поклонясь до земли, и грибка не поднять. Точка минимума Чем дальше в лес, тем больше дров. Возрастание |
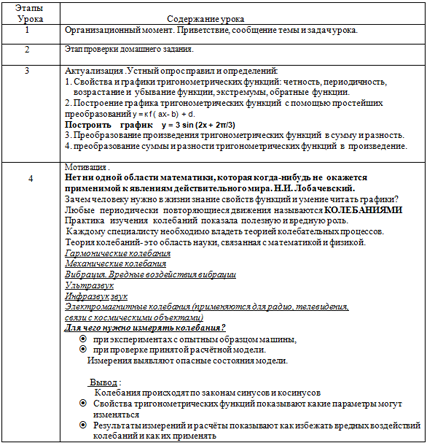
| 6 | Тестирование (индивидуальная работа) Тест 1 вариант 1.Вдоль какой оси сжимается график функции у= cos 2x А) вдоль оси Ох В) вдоль оси Оу 2.Вдоль какой оси растянется график функции у= 4cos x А) вдоль оси Ох В) вдоль оси Оу 3. график функции у= cos x +3 смещается А) вправо В) влево С) вверх D)вниз 4. график функции у= tg (х+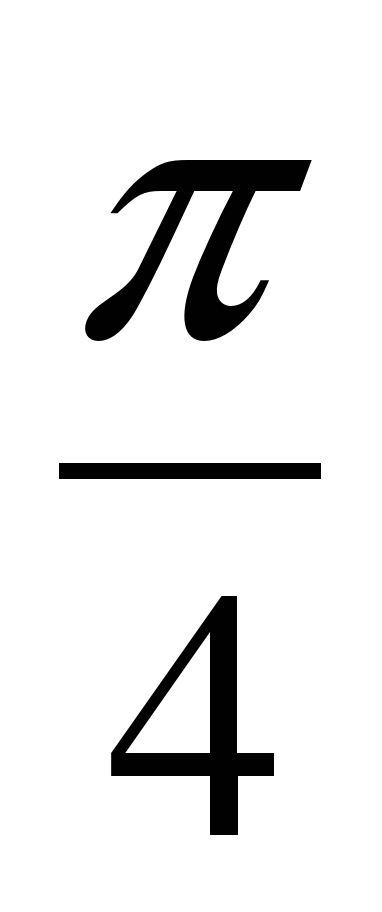 ) смещается А) вправо В) влево С) вверх D)вниз ) смещается А) вправо В) влево С) вверх D)вниз 5. график функции у =sin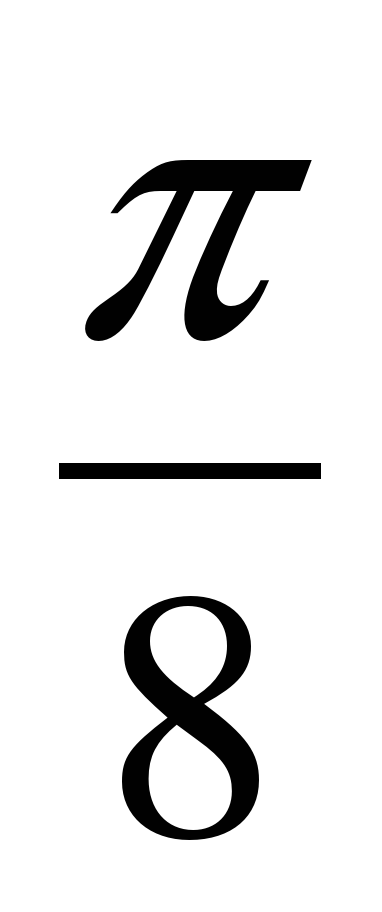 х растягивается или сжимается вдоль оси А) растягивается В) сжимается х растягивается или сжимается вдоль оси А) растягивается В) сжимается 6.Вычислие период функции y = 3 cos 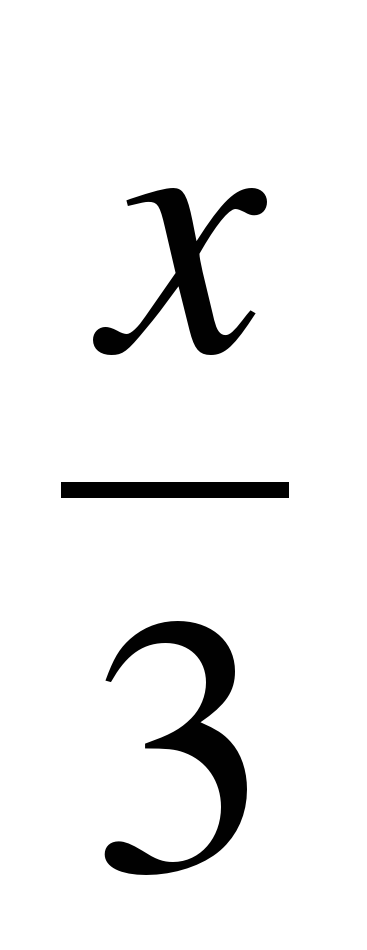 – 1 А) – 1 А) 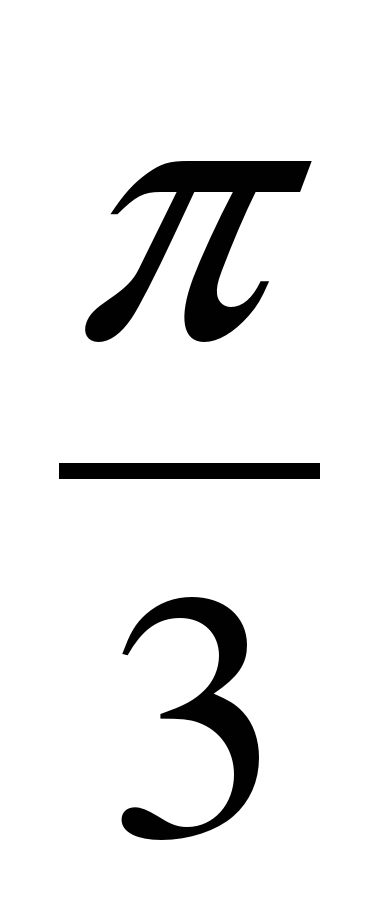 В) В)  С) С) 
Тест 2 вариант 1.Вдоль какой оси растянется график функции у= 3cos x А) вдоль оси Ох В) вдоль оси Оу 2.Вдоль какой оси сжимается график функции у= cos 4x А) вдоль оси Ох В) вдоль оси Оу 3. график функции у= cos (х - 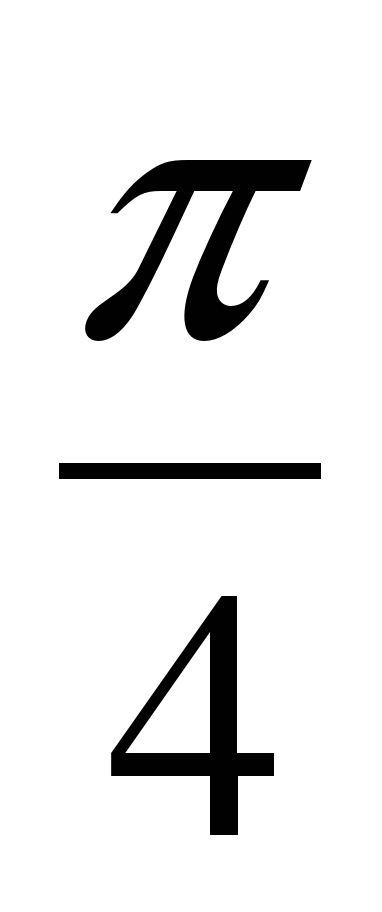 ) смещается А) вправо В) влево С) вверх D)вниз ) смещается А) вправо В) влево С) вверх D)вниз 4. график функции у= cos х - 5 смещается А) вправо В) влево С) вверх D)вниз 5. график функции у =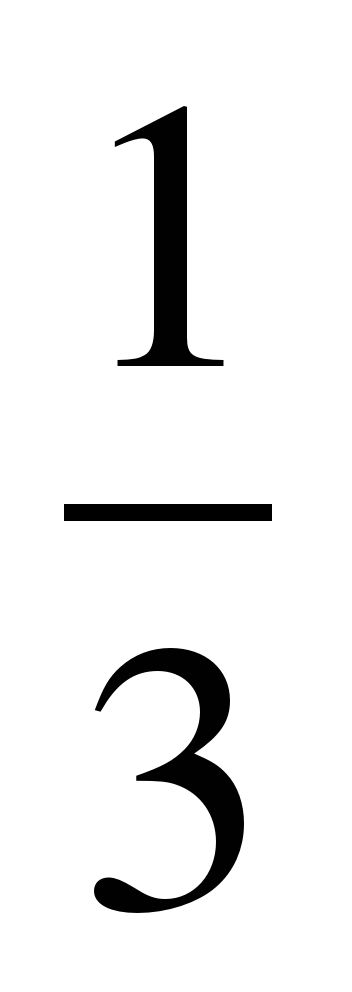 sinх растягивается или сжимается вдоль оси А) растягивается В) сжимается sinх растягивается или сжимается вдоль оси А) растягивается В) сжимается 6.Вычислие период функции y = 3 cos (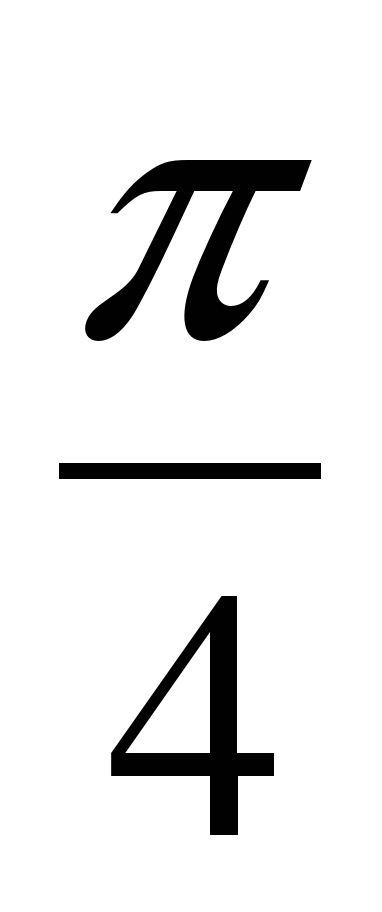 + 5x) – 1 А) + 5x) – 1 А) 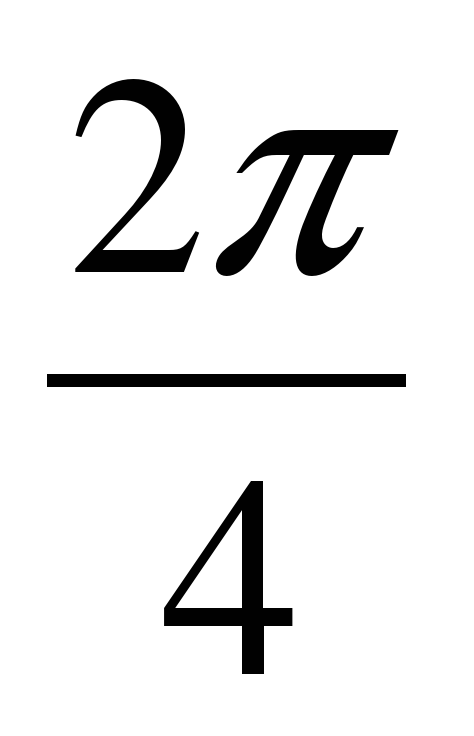 В) В)  С) С) 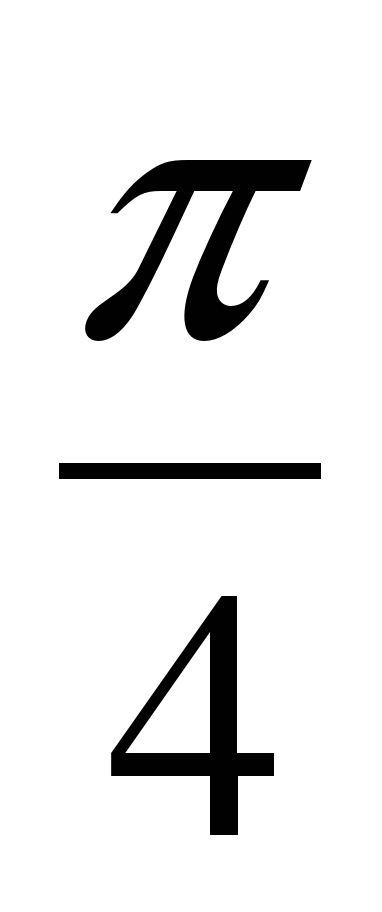 D) D)  |
| 7 | Этап информации о домашнем задании прочитать, выучить правила, построение графика функции а) y = cos 2x б) y = sin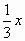
|
| 8 | Подведение итогов урока. Выставление оценок. |
| 9 | Рефлексия. Какие основные свойства тригонометрических функций мы сегодня рассматривали на уроке? |
Объявляется количество баллов, полученных каждой командой.
Оценка за самостоятельную работу объявляется на следующем уроке.
| № | Ф.И.О.
| Задания | Итог |
| 1 | 2 | 3 | 4 | 5 |
| Термины, рзминка апо теории | Кластер
| Построение графика | Проявите смекалку | тест | Баллы | Оценка |
| 1 |
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
| Итог |
|
|
|
|
|
|
|
| Общее количество баллов |
|
|
Оценка «5» ставится, еслииученик набрал и большее количество баллов; оценка «4» баллов; оценка «3» - баллов.
Коллективная работа Разминка (устная).
Какие преобразования нужно выполнить, чтобы построить график данной функции?
1) f(x) = 0,5 cos x сжатие по оси Оу
2) f(x) = 3 + sin x вверх на 3 единицы по оси Оу
3) f(x) = sin (x - П/4) вправо по оси Ох
4)f(x) = cos x /2 растяжение по оси Ох в 2 раза
1группа.
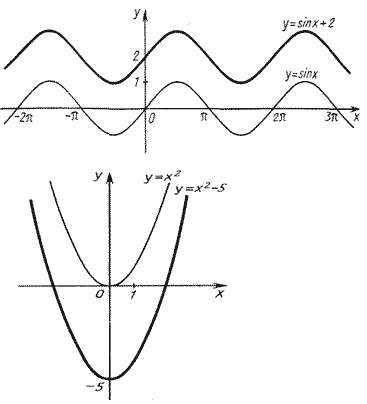
Для построения графика функции f (x) + b, где b - постоянное число, надо перенести график f на вектор (0; b) вдоль оси ординат. Например: а) y = sin x + 2; б) y = x2 - 5;
2 группа Для построения графика функции y = k f (x) надо растянуть график функции y = f (x) в k раз
вдоль оси ординат. Например: б) y=3cosx
3 группа
Для построения графика функции y = f надо подвергнуть график функции f растяжению
коэффициентом k вдоль оси абсцисс. Например: а) y = cos 2x б) y = sin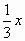

 Получите свидетельство
Получите свидетельство Вход
Вход














 Свойства и графики тригонометрических функций (разработка урока) (97.5 КB)
Свойства и графики тригонометрических функций (разработка урока) (97.5 КB)
 0
0 1910
1910 372
372 Нравится
0
Нравится
0


