Министерство сельского хозяйства и продовольствия Самарской области
государственное бюджетное профессиональное
образовательное учреждение Самарской области
"Кинель - Черкасский сельскохозяйственный техникум"
ТЕСТИРОВАНИЕ - КАК ОДИН ИЗ МЕТОДОВ КОНТРОЛЯ ЗНАНИЙ
План
Аннотация
Пояснительная записка
Целевое назначение
Содержание:
Принципы обучения
Индивидуально – тематический учёт знаний, умений и навыков студентов
Контроль и уровни усвоения знаний
Виды контроля
Методы контроля
Формы контроля
Оценка знаний, умений и навыков студентов
Тестирование как метод контроля знаний
Тесты (из опыта работы)
Заключение
Аннотация
В методической разработке рассмотрен один из видов контроля – тестирование. В практику всё чаще входит проверка знаний учащихся посредством тестов (аттестация школьников, аттестация студентов, аттестация учебных заведений). Такой вид проверки широко применяется и при проведении вступительных экзаменов. Наши студенты, достаточно подготовленные школой к написанию традиционной контрольной работы, плохо справляются с выполнением теста, т.к. испытывают дискомфорт из-за непривычного вида заданий. Одним из решений этой проблемы является предложение использовать для тематического контроля знаний студентов по математике тесты.
Данная методическая разработка может быть рекомендована преподавателям математики, а, также преподавателям других дисциплин, в качестве рекомендаций по составлению и применению тестов на уроках.
Количество страниц – 62.
Автор: преподаватель математики ГБПОУ «Кинель – Черкасского сельскохозяйственный техникум» Кузнецова Л.В.
Пояснительная записка
Методическая разработка «Тестирование – как один из методов контроля знаний» является обобщением моего опыта работы в качестве преподавателя математики, а, также изучение современной педагогической литературы по проблеме контроля знаний и умений студентов. Данная методическая разработка раскрывает один из важнейших элементов учебного процесса – контроль знаний и умений студентов. От его правильной организации во многом зависит эффективность управления учебным процессом и качество подготовки специалиста. Обучение не может быть полноценным без регулярной и объективной информации о том, как усваивается студентами материал, как они применяют полученные знания для практических задач. Благодаря контролю между преподавателем и студентами устанавливается «обратная связь», которая позволяет оценивать динамику усвоения учебного материала, действительный уровень владения системой знаний, умений и навыков и на основе их анализа вносить соответствующие коррективы в организацию учебного процесса.
Контроль знаний и умений студентов выполняет в процессе обучения проверочную, обучающую, развивающую, воспитательную и методическую функции. Наиболее важная и специфическая – проверочная функция. Показатели контроля служат главным основанием для суждения о результатах учения, т.е. для решения таких вопросов, как перевод на следующий курс, выдача диплома. Правильно организованный контроль знаний и умений служит как целям проверки, так и целям обучения. В ходе выполнения контрольных заданий происходит повторение и закрепление, совершенствование приобретённых ранее знаний путём их уточнения и дополнений, студенты переосмысливают и обобщают пройденный материал, использую знания в практической деятельности. Контроль способствует формированию умений и навыков рационально организовывать учебную деятельность, самостоятельно овладевать знаниями. Развивающая функция контроля заключается в том, что он даёт большие возможности для развития личности студентов, формирования его познавательных способностей, т.к. в этом процессе происходит напряжение умственной деятельности. Контроль протекает в условиях обострённой работы внимания, памяти, мышления, воображения. Контроль знаний и умений решает и воспитательную функцию, т.к. он всегда глубоко затрагивает эмоциональную сферу личности. Контроль дисциплинирует студента, воспитывает у него чувство ответственности за свою работу, приучает к систематическому учебному труду, стимулирует регулярную активную учебную деятельность, серьёзное и добросовестное отношение к ней. Контроль знаний и умений выполняет методическую функцию. Его процесс и результаты очень важны для совершенствования работы самого преподавателя.
В данной методической разработке большое внимание уделено тестированию, как одному из современных методов контроля знаний и умений.
Целевое назначение
Процесс обучения математике не может быть эффективным без постоянной обратной связи (студент – преподаватель), дающей преподавателю информацию об уровнях усвоения материала, о знаниях, умениях и навыках студентов, о возникающих у них трудностях, без преодоления которых невозможно сознательное и прочное усвоение курса. контроль как раз и позволяет преподавателю осуществить обратную связь и использовать её для того, чтобы выяснить, достигнута ли цель обучения.
Существует 3 вида контроля: внешний контроль преподавателя за деятельностью студента, самоконтроль и взаимопроверка. В своей методической разработке я остановлюсь в основном на внешнем контроле, его видах, организационных формах и методике проведения.
Проверка знаний, умений и навыков учащихся на занятиях математики неоднократно обсуждалась в педагогической и методической литературе, но до сих пор в этом вопросе встречается много противоречий, затрудняющих выбор наиболее целесообразной и рациональной системы контроля.
Существующая традиция накопления отметок в классном журнале нередко ориентирует преподавателя на выставление бессистемных и случайных баллов, не позволяющих правильно оценить учебную деятельность студента.
Опыт показывает, что в современных условиях целесообразно организовать индивидуально – тематический учёт знаний, умений и навыков, при котором каждый студент оценивается по всем основным разделам любой темы курса. Успешному осуществлению такой системы контроля способствует компьютеризация обучения.
В данной методической разработке раскрывается методика индивидуально – тематического учёта знаний, умений и навыков студентов усвоения математики. В основу системы контроля положен опыт моей работы, а также изучение и обобщение педагогического опыта.
Содержание
1) Принципы обучения
Принципы обучения – это исходные дидактические положения, которые отражают протекание объективных законов и закономерностей процесса обучения и определяют его направленность на развитие личности. В принципах обучения отражаются теоретические подходы к построению учебного процесса и управлению им. Они определяют позиции и установки, с которыми преподаватели и учителя подходят к организации процесса обучения и к поиску возможностей его оптимизации.
Все принципы обучения связаны друг с другом и проникают один в другой, поэтому они могут быть представлены как единая система содержательных и процессуальных (организационно – методических) принципов. Такое их деление условно: значение каждого принципа не ограничивается только рамками своей группы. Из дидактических принципов вытекают правила обучения, которые подчиняются принципу, конкретизируют его, определяют характер отдельных методических приёмов, используемых преподавателями (учителями), и ведут к реализации данного принципа. Принципы отражают сущность процесса обучения, а правила – его отдельные стороны. Содержательные принципы обучения отражают закономерности, которые связаны с отбором содержания образования и его совершенствованием. К ним относятся принципы: гражданственности, научности, воспитывающего характера, фундаментальности и прикладной направленности.
Организация и методика обучения регламентированы действием закономерностей социального, психологического и педагогического характера, знание которых позволяет сформулировать организационно – методические принципы обучения: преемственности, последовательности и систематичности; единства группового и индивидуального обучения; соответствия обучения возрастным и индивидуальным особенностям обучаемых; сознательности и творческой активности; доступности при достаточном уровне трудности; продуктивности и надёжности.
При создании и применении тестов в учебной деятельности мною используются следующие принципы обучения:
Организационно – методические принципы обучения.
принцип преемственности, последовательности и систематичности. Он достигается последовательным переходом от решения простых задач к сложным, а также обеспечивается системным построением рабочей программы и установлением межпредметных и внутрипредметных связей (например, тесты по теме «Тригонометрические функции» даются в последовательности от простых к более сложным: «Тригонометрические функции» → «Свойства и графики тригонометрических функций» → «Простейшие тригонометрические уравнения и неравенства» → «Тригонометрические уравнения и неравенства»).
принцип доступности. Реализация этого принципа достигается за счёт дифференцированного подхода к обучению студентов (тесты, предлагаемые, студентам имеют разные уровни сложности, в зависимости от подготовки студентов.)
принцип индивидуального обучения. Обучение не может быть успешным, если игнорируются индивидуальные особенности обучаемых, трудности, испытываемые каждым, различия в темпе и степени усвоения материала и др. Это означает, что наряду с групповыми формами обучения следует применять и индивидуальное обучение. Формами индивидуализации обучения являются индивидуализированные творческие задания, индивидуальные консультации и собеседования, самостоятельная учебная работа и др. Работа с тестами, как раз и есть один из приёмов индивидуального обучения.
принцип сознательности и активности. Активность обучаемых может иметь репродуктивный или творческий характер. В первом случае она направлена на запоминание и воспроизведение изучаемого материала, выполнение учебных заданий по образцам и алгоритмам. Реализация данного принципа предполагает развитие инициативы студентов и их самодеятельности (например, в качестве домашнего задания студентам предлагалось самим составить небольшие тесты из 4-5 вопросов по пройденному материалу).
Содержательные принципы обучения:
1) принцип научности. При реализации данного принципа педагогические воздействие должно быть направлено на развитие у студентов познавательной активности и дивергентного мышления, творчества, ознакомление их со способами научной организации учебного труда. Этому способствует использование проблемных ситуаций, в том числе ситуаций личностного выбора, а также специальное обучение умению наблюдать явления, фиксировать и анализировать полученные результаты, вести научную дискуссию, доказывать свою точку зрения, работать с научной и учебной литературой.
2) принцип прикладной направленности. Содержание образования, согласно данному принципу, должно отражать преобразования в экономике, политике, культуре, т.е. в том реальном социальном контексте, в котором протекает жизнедеятельность обучаемых (например, тесты по применению производной «Решение задач прикладного характера» - показывают межпредметные связи математики с другими дисциплинами: экономикой, физикой, химией и др.)
3) принцип фундаментальности. Фундаментальность в обучении предполагает научность, полноту и глубину знаний. Она обусловлена характером компьютеризации современного общества, требующего от человека высоко – интеллектуальной мобильности, исследовательского склада мышления, желания и умения постоянно пополнять свои знания по мере происходящих в жизни и деятельности изменений. Фундаментальные знания обладают способностью медленнее устаревать, чем знания конкретные. Они апеллируют не столько к памяти, сколько к мышлению человека (например, тесты по «Стереометрии»).
4) принцип прочности. Он достигается путём эффективной реализации вышеперечисленных принципов обучения, а также с помощью систематического контроля и оценки, приобретённых студентами знаний, умений и навыков (зачёты, опросы, тесты и т.п.)
2) Индивидуально – тематический учёт знаний, умений и навыков студентов
Оценка знаний, умений и навыков студентов до сих пор остаётся в какой – то степени субъективной, несмотря на широкое освещение этого вопроса в методической литературе. Так, она может зависеть от личности учителя. За одну и ту же работу студент у различных преподавателей может получить разные отметки.
Отметка может быть выставлена за доказательство теоремы или решение трудной задачи, а в ряде случаев – только за ответы на простые вопросы или за решение несложной задачи. Таким образом, по выставленным в классном журнале баллам практически невозможно судить о фактическом уровне знаний, умений и навыков студентов.
Обычно полагается, что у каждого студента должно быть много отметок и что итоговая отметка зависит от количества отметок, выставленных в журнале. Однако и это не отражает истинного уровня знаний студента.
Возникает закономерный вопрос, каким образом организовать такой контроль, который позволял бы преподавателю управлять процессом обучения, совершенствовать знания, умения и навыки студентов и определять фактический уровень усвоения материала. Этим требованиям удовлетворяет, на мой взгляд, контроль с индивидуально – тематическим учётом знаний, при котором уровень знаний, умений и навыков каждого студента проверяется и фиксируется по каждой теме.
Изучая, например, на первом курсе техникума тему «Производная» студенты должны знать:
определения: возрастающей и убывающей функции, производной, дифференцируемой функции, критической точки, точек максимума и минимума;
формулы дифференцирования суммы, произведения, частного и степенной функции;
правило дифференцирования сложной функции;
формулу Δ f (x0) ≈ f ' (x0) · Δ x;
формулу касательной к графику функции f(x) в данной точке х0 ;
необходимое и достаточное условие существования экстремума функции;
схему исследования функции;
физический и геометрический смысл производных первого и второго порядка.
Нужно обучить студентов умениям:
находить промежутки возрастания и убывания функции;
приращение функции;
производные функций по формулам;
промежутки монотонности и экстремумы;
наибольшее и наименьшее значения функций на заданном промежутке;
составлять уравнение касательной к заданной кривой;
решать задачи, связанные с нахождением наименьших и наибольших значений;
выполнять исследование функции.
Планируя изучение темы, преподаватель устанавливает способы проверки. Так, например, умения 3 и 4 из темы «Производная» можно проверить с помощью письменной контрольной работы, умения 1 – с помощью тестов и математических диктантов, умения 2 – путём опроса у доски.
При индивидуально – тематическом учёте знаний комбинированные контрольные работы, содержащие задачи из разных тем, проводятся только в конце семестра или года, т.к. оценка такой работы является интегральной, не дающей ясной информации об уровне усвоения студентом той или иной темы. Только, отметки «5» или «2» в этом случае являются информативными: первая говорит о том, что студент усвоил все темы, вторая свидетельствует о серьёзный пробелах в знаниях студентов.
Для индивидуально – тематического учёта можно предложить следующий, так называемый, лист учёта:
Тема (название).
| № п/п | Ф. и. студента. | Знания. | Умения. | Ведение конспекта. |
| 1 | 2 | …….. | 1 | 2 | ……. |
|
|
|
|
|
|
|
|
|
|
|
Из листа учёта студенты видят, над, чем им следует работать. Поскольку перенос отметок в журнал происходит с некоторой задержкой, студент имеет возможность улучшить свою отметку. Лист индивидуально – тематического учёта воспитывает у студентов навыки самоконтроля и заставляет серьёзнее относиться к учёбе.
Индивидуально – тематический учёт знаний позволяет преподавателю легко выставлять семестровые или годовые отметки, т.к. лист учёта наглядно показывает усвоение студентами программы.
3) Контроль и уровни усвоения знаний
В педагогической литературе нет единой точки зрения об уровнях усвоения материала, потому, что часть материала рассматривается в ознакомительном плане, часть – требует глубоких и прочных знаний, умений и навыков. Поэтому нельзя говорить о контроле на занятиях математики вообще: речь может идти только о проверке усвоения тех или иных математических знаний на вполне определённом уровне, повышающемся в процессе обучения. Особенности преподавания математики требуют, чтобы преподаватель при проверке знаний исходил из вполне определённой модели усвоения математических знаний. Такая модель изложена Столяром А.А.1 , который предложил 3 уровня усвоения:
Уровень А – уровень воспроизведения, предусматривает знание учащимися простейших математических фактов и правил решения стандартных задач.
| Усвоение знаний на уровне А. | Проверка знаний, умений и навыков на уровне А. |
знание простейших математических фактов; знание терминологии; умение пользоваться простейшими правилами операций и алгоритмами; воспроизведение понятий со всеми существенными признаками. | Выяснение насколько правильно учащиеся воспроизводят определения или распознают понятия в несложных ситуациях. |
Уровень В – уровень понимания предусматривает знание учащимися понятий и отношений между ними и применение знаний в стандартных условиях.
| Усвоение знаний на уровне В. | Проверка знаний, умений и навыков на уровне В. |
знание понятий и отношений между ними; умение распознать понятие в стандартных ситуациях; применение полученных знаний в стандартных условиях или при небольших отклонениях от них; перевод задачи на язык математики и решение её; умение делать простые обобщения; воспроизведение описания изученных ситуаций на математическом языке; понимание изученной математической структуры. | Выяснение умений решать по данному алгоритму задачи или упражнения по приведённому образцу и распознавать понятие в ситуациях, стандартных или незначительно отличающихся от них. |
Уровень С – уровень переноса, предусматривает применение знаний в нестандартных условиях, умение анализировать сложные ситуации и находить новые доказательства известных математических фактов.
| Усвоение знаний на уровне С. | Проверка знаний, умений и навыков на уровне С. |
распознавание понятий в новой нестандартной ситуации; применение знаний в нестандартных ситуациях; умение решать нестандартные задачи; умение анализировать предложенные доказательства; возможность самостоятельного открытия новых математических фактов, доказательства теорем и т.д. | Распознавание понятий в нестандартной ситуации и решение нестандартных задач. |
На мой взгляд – приведённая модель достаточно чётко устанавливает различные уровни усвоения понятий в математике.
4) Виды контроля
В педагогической литературе обычно выделяют 4 вида контроля: предварительный, текущий, рубежный (периодический), итоговый. Основанием для выделения этих видов контроля является специфика дидактических задач на различных этапах обучения: текущий контроль проводят в процессе усвоения нового учебного материала; рубежный применяют для проверки усвоения значительного объёма изученного материала (темы, раздела); с помощью итогового контроля выявляют степень овладения учебным материалом по предмету, ряду дисциплин (на экзаменах, приёме курсового проекта, защите дипломного проекта).
Предварительный контроль служит необходимой предпосылкой для успешного планирования и руководства учебным процессом, т.к. он позволяет определить исходный уровень знаний и умений студентов, чтобы использовать его как фундамент.
Текущий контроль является одним из основных видов проверки знаний, умений и навыков студентов. Задача текущего контроля - регулярное управление учебной деятельностью студентов и её корректировка. Другими важными задачами текущего контроля являются: стимуляция регулярной, напряжённой и целенаправленной работы студентов, активизация их познавательной деятельности; определение уровня овладения студентами самостоятельной работы, создание условий для их формирования.
Периодический (рубежный) контроль позволяет определить качество изучения студентами учебного материала по разделам, тема предмета. Такой контроль проводят обычно несколько раз в семестр (контрольные работы, зачёты, учётно – обобщающие уроки и т.п.). Периодический контроль позволяет проверить прочность усвоения полученных знаний и приобретённых умений; при этом виде контроля охватываются большие по объёму разделы курса и от студентов требуется большая самостоятельная конструктивная деятельность. Рубежный контроль охватывает всех студентов и проводится в виде устного опроса, небольших письменных, графических, практических работ.
Итоговый контроль направлен на проверку конечных результатов обучения, выявление степени овладения студентами системой знаний, умений и навыков, полученных в процессе изучения отдельного предмета или ряда дисциплин. Итоговый контроль – это контроль интегрирующий, именно он позволяет судить об общих достижениях студентов. При подготовке к нему происходит более углубленное обобщение и систематизация усвоенного материала, что позволяет поднять на новый уровень знания и умения студентов. Итоговый контроль осуществляется на переводных и семестровых экзаменах, квалификационных испытаниях, государственных экзаменах, защите дипломного проекта.
5) Методы контроля
Методы контроля – это способы деятельности преподавателя и студентов, в ходе которых выявляются усвоение учебного материала и овладение студентами, требуемыми знаниями, умениями и навыками.
Основными методами контроля являются:
Устный опрос: фронтальный, индивидуальный, комбинированный).
фронтальный опрос проводится в форме беседы преподавателя с группой. Он сочетается с повторением пройдённого, являясь средством для закрепления знаний и умений. Его достоинство в том, что в активную умственную работу можно вовлечь всех студентов группы. С помощью фронтального опроса преподаватель имеет возможность проверить выполнение студентами домашнего задания, выяснить готовность группы к изучению нового материала, определить сформирован ость основных понятий, усвоение нового учебного материала, который только, что был разобран на занятии. Целесообразно использовать фронтальный опрос также перед проведением ПЗ и ЛПЗ, т.к. он позволяет проверить подготовленность студентов к их выполнению.
индивидуальный опрос предполагает обстоятельные, связные ответы студентов на вопрос, относящийся к изучаемому материалу, поэтому он служит важным средством развития речи, памяти и мышления студентов. Вопросы обычно задают всей группе и после небольшой паузы, необходимой для того, чтобы все студенты поняли его и приготовились к ответу, вызывают для ответа конкретного студента. Для того, чтобы группа слушала ответ своего товарища, используют разные приёмы: предлагается составить план ответа, оценить ответ, составить рецензию ответа товарища, постановка вопросов студенту, отвечающему у доски.
комбинированный или уплотнённый опрос сочетает устный опрос с другими методами: с письменным опросам по карточкам, с самостоятельной работой. Все это позволяет проконтролировать работу большого количества студентов.
Письменная проверка. Применение этого метода даёт возможность в наиболее короткий срок одновременно проверить усвоение учебного материала всеми студентами группы, определить направления для индивидуальной работы с каждым. Письменная проверка используется во всех видах контроля и осуществляется как в аудиторной, так и во внеаудиторной работе (домашние задания). Письменные работы по содержанию и форме могут быть самыми разнообразными: диктанты, сочинения, ответы на вопросы, решение задач и примеров, составление тезисов, подготовка рефератов и докладов, тесты.
Практическая проверка занимает особое место в системе контроля. Практическая проверка позволяет выявить, как студенты умеют применять полученные знания на практике, насколько они овладели необходимыми умениями, главными компонентами деятельности. Для практической проверки используются самые разнообразные задания: выполнить практическую работу, проанализировать ситуацию, поставить эксперимент и т.д.
Стандартизованный контроль предусматривает разработку тестов. Тест состоит из двух частей – задания и эталона. Задание выдаётся студентам для выполнения, эталон представляет собой образец правильного и последовательного выполнения задания. Тестовый контроль даёт возможность при незначительных затратах аудиторного времени проверить всех студентов.
Самоконтроль и взаимопроверка. Самоконтроль активизирует познавательную деятельность студентов, воспитывает сознательное отношение к проверке, способствует выработке умений находить и исправлять ошибки. Все это необходимо для формирования навыков самообразования. Перед самостоятельной работой студенты получают инструкцию о выполнении работы и ключ для самопроверки. Инструкция должна показать студентам, какие знания и умения контролируются, а ключ содержит правильные ответы, по которым студенты сверяют результаты работы и вносят необходимые исправления. Подобным образом осуществляется и взаимопроверка, в ходе которой студенты проверяю друг у друга выполнение задания.
6) Формы контроля
Контрольные работы проводятся, в основном, после завершения изучения тем или узловых вопросов, особо значимых для усвоения других учебных дисциплин.
Зачёт служит одной из форм контроля за выполнением ПЗ и ЛПЗ, а также, применяется в период производственной практики.
Квалификационные испытания предназначены для проверки сформированности знаний, умений и навыков по рабочей специальности.
Семестровые и переводные экзамены являются ведущими, наиболее значительными формами организации контроля. В ходе их проводится итоговая проверка результатов учебной деятельности студентов по изучению конкретной дисциплины, выявляется уровень сформированности знаний и умений.
Курсовое и дипломное проектирование выполняет как обучающую так и контролирующую функции и является важнейшей формой проверки овладения студентами теоретическими знаниями, практическими умениями и навыками.
Государственные экзамены – заключительная форма контроля, направленная на комплексную проверку подготовки будущего специалиста к работе, на определение степени овладения знаниями, умениями и навыками в соответствии с характером профессиональной деятельности.
7) Оценка знаний, умений и навыков студентов
Результаты контроля знаний и умений студентов выражаются в оценке. Оценка – это определение и выражение (в баллах, а также оценочных суждениях преподавателя) степени усвоения студентами знаний и умений, установленных программой. Оценка имеет большое образовательное и воспитательное значение. Она является характеристикой результатов учебной деятельности студента, даёт представление о состоянии знаний и умений и степени их соответствия требованиям контроля, осведомляет студента о том, какого мнения о нём преподаватель. Всё это корректирует самооценку студента.
При оценке знаний нужно учитывать, на каком уровне студент усвоил тот или иной вопрос, соответствует ли этот уровень тому, который определён программой, и выставлять студенту балл, исходя из норм оценки знаний, умений и навыков. Нормы оценки успеваемости основываются на критериях полноты, осознанности и действенности знаний, умений и навыков.
Если студент дал исчерпывающий ответ на основной вопрос, сформулировал определения и указал существенные признаки понятий, ответил на дополнительные вопросы, то такой ответ удовлетворяет требованиям полноты и студенту выставляется балл «5»; при неточностях несущественного характера студент получает «4», а при наличии только общего представления по каждому из признаков и исправлении ошибок с помощью преподавателя – отметку «3». Осознанность усвоения математических знаний означает умение указать на взаимосвязь понятий, установить их сходство и различие, систематизировать и обобщать материал. Действенность усвоения материала означает умение выполнять упражнения и применять изученный материал в жизненных ситуациях. Руководствуясь нормами оценки, следует иметь в виду, что окончательное заключение об уровне знаний студентов предполагает определение конкретных требований к устному ответу или письменной работе. Перед оценкой ответ студента анализируется, выясняется характер и происхождение ошибок.
Возможны следующие формы проверки знаний студентов: 1) наблюдения, дающие представление о работе студента; 2) текущая (письменная или устная) проверка с учетом дифференцированного подхода в обучении; 3)экзаменационно – зачётная проверка (на зачёте или экзаменах).
При оценке знаний и умений студентов преподавателю необходимо соблюдать некоторые требования:
объективность. Оценка должна отражать действительный уровень усвоения учебного материала, предусмотренного программой, а также то, насколько сознательно и прочно студент владеет этим материалом, самостоятельно его использует.
индивидуальный характер. Это значит, что оценка фиксирует результат сугубо индивидуального процесса, уровень знаний конкретного студента.
гласность. Оценка, будучи оглашённой, оказывает воздействие прежде всего на студента, которому она дана, т.к. он получает корректирующую информацию. Однако оценка оказывает воздействие и на всю учебную группу: позволяет другим студентам соотнести знания и умения с требованиями контроля, влияет на мнение товарищей об отвечающем, выливается в форму сооценки со стороны.
обоснованность. Оценка должна быть мотивированной и убеждающей, правильно соотноситься с самооценкой и мнением коллектива студентов.
Традиционной педагогикой разработаны критерии количественной пятибалльной системы оценки знаний, умений и навыков. В традиционном обучении выразительным критерием выступает педагог: как он оценил ответ или деятельность студента, такая оценка и будет выставлена в журнал. Студент не имеет никакой возможности принять участие в этом процессе. В инновационном обучении выразителем критериев выступают преподаватель и студент. Эффект от такого сотрудничества значительно возрастает, если применить само- и взаимоконтроль и само - и взаимооценку. Например. после ответа преподаватель спрашивает студента какую оценку он поставил бы себе (дать обоснование). Затем преподаватель обращается к группе с просьбой оценить в баллах ответ товарища и аргументировать предлагаемую оценку. В итого, с учётом мнения преподавателя , выставляется оценка. Вовлечение студентов в оценочную деятельность значительно облегчает работу преподавателя. Активизации этого процесса способствует вооружение студентов критериями, руководствуясь которыми они будут вести оценку и самооценку. Студент должен уметь сравнивать свои знания и знания товарищей с заданным образцом и на основании этого вести взаимо – и самооценку. С этой целью в кабинете «Математика» есть стенд «Требования к уровню обучения».
8) Тестирование как метод контроля знаний
а) Виды тестов
Обучение может быть эффективным только в том случае, если существует надёжная обратная связь от студента к преподавателю, дающая достоверную информацию о восприятии и усвоении материала студентами.
Традиционные формы контроля не достаточно оперативны, и для их осуществления требуется значительное время, поэтому возникает необходимость в новых видах проверки знаний. Распространение компьютеризации способствовало тому, что преподаватели математики при проверке знаний стали обращаться к заданиям с выборочными ответами, к тестам.
Тест представляет собой кратковременное технически сравнительно просто обставленное испытание, проводимое в равных для всех испытуемых условиях и имеющее вид такого задания, решение которого поддаётся качественному учёту и служит показателем степени развития данного испытуемого.
Тест состоит из системы заданий, к каждому из которых прилагаются как верные, так и неверные ответы. Из них студент выбирает тот, который считает верным для данного вопроса. При этом неверные ответы содержат такую ошибку, которую студент может допустить, имея определённые пробелы в знаниях. Иногда такие тесты называют избирательными. Избирательные тесты могут быть различными:
многовариантные тесты, в которых среди предлагаемых ответов на вопрос приведено несколько неверных и единственный верный ответ;
многовариантные тесты с несколькими верными и неверными ответами на вопрос;
альтернативные тесты с двумя ответами на вопрос (один ответ верный, другой – содержит ошибку).
Существуют тесты на завершение, в которых приведены предложения с пропусками слов.
Имеются тесты перекрёстного выбора, в которых требуется установить соответствие между элементами множества ответов.
Встречаются также тесты идентификации, в которых в качестве ответов приводятся графики, схемы, чертежи т.д.
Тестирование является стандартизированной формой контроля, т.к. процедура проведения теста и оценка знаний единообразны (стандартны) для всех студентов. Но при тестировании как и при любом методе контроля знаний, необходимо осуществлять дифференцированный подход к студентам.
Достоинства теста:
оперативно выявляет знания, умения и навыки студентов, а также понимание ими закономерностей, лежащих в основе изучаемых фактов;
позволяет в течение короткого времени получить представление о пробелах в знаниях и помогает организовать работу по предупреждению отставания студентов;
предоставляет преподавателю возможность проверять знания, умения и навыки на разных уровнях и осуществлять дифференцированное обучение;
способствует рациоанльному использованию времени на занятии;
активизирует мышление студентов;
даёт возможность преподавателю критически оценить свои методы преподавания.
Однако тест фиксирует только результаты работы, но не ход её выполнения, возможно угадывание правильного ответа, а также случаи, когда выбор неверного ответа объясняется невнимательностью студента, поэтому рациональнее сочетать тестирование с различными формами традиционного контроля.
При тестировании целесообразно придерживаться следующих рекомендаций:
предлагать задания ниже той максимальной сложности, которая была достигнута на занятиях;
вопросы, входящие в тест, должны быть примерно одинаковой степени сложности;
в каждом вопросе стремиться предлагать одинаковое количество ответов, но разное число верных и неверных;
по возможности пользоваться тестированием на ПК;
тесты можно использовать на разных этапах урока.
Тестированием можно охватить проверку усвоения одного правила, свойства или формулы, параграфа, темы, большого раздела.
b) Составление тестов
Рекомендации по составлению тестов:
тесты для студентов 1-го курса должны иметь один правильный ответ в общем числе 3-4 ответов; для студентов старших курсов допустимо 2-3 правильных ответов в системе 4-5 ответов;
тест должен быть составлен корректно (например, если вопрос задаётся в единственном числе, ответ должен быть только один);
тест не должен иметь двусмысленных формулировок, неясностей, не должен допускать громоздких фраз, большого описания и т.д.;
ответы на тест не должны допускать приблизительности, т.е. цифры, размеры должны даваться в тестах в тех же границах, что и в лекциях;
компоновать тесты блоками;
составлять тесты необходимо в таком объёме, чтобы выполнение контрольного и тренировочного вариантов не занимало более 45 минут;
чем больше тестовая программа по объёму, тем короче должна быть формулировка вопросов и ответов;
проводить тестирование как зачёт по теме или допуск к ПЗ, ЛПЗ, производственной практике, экзамену и т.п.
9) Тесты
1. Тема: «Прямые и плоскости в пространстве».
Цель: проверка знаний студентов по теме «Прямые и плоскости в пространстве» (зачётная работа).
1 вариант.
Сколько существует плоскостей, проходящих через данные прямую и точку в пространстве?
а) 0 (ни одной), б)1 , в) (бесконечно много),
г)0 или , д) 1 или .
(2-3).
Точки К,Е,М,Н- середины рёбер АВ, ВС, СD, DА тетраэдра АВСD(рис.1)
Каково взаимное расположение прямых КЕ и МН?
а) пересекаются, б) параллельны, в) скрещиваются,
г) могут быть пересекающимися, параллельными и скрещивающимися (в зависимости от вида тетраэдра).
Каково взаимное расположение прямых КМ и ВС?
а) пересекаются, б) параллельны, в) скрещиваются, г) возможны все три случая а) -в).
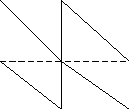 рис. №1.
рис. №1.
(4-7).
Дан прямоугольный параллелепипед АВСDА1 В1 С1 D1( рис.2).
Каково взаимное расположение прямых АВ и ВD?
а) скрещиваются, б) пересекаются, в) параллельны, г) пересекаются или параллельны.
Какие из прямых ВВ1, СС1 , D1С1 скрещиваются с прямой АВ?
а) только ВВ1, б) только СС1 , в) только ВВ1 и СС1 , г) только СС1 и D1С1, д) все три прямые.
Каково взаимное расположение прямой ВС и плоскости ВDА?
а) параллельны, б) пересекаются, в) пересекаются или параллельны (т.е. могут и пересекаться и быть параллельными).
Каково взаимное расположение плоскостей ВDА и ВDС?
а) параллельны, б) пересекаются, в) пересекаются или параллельны.
 рис. № 2.
рис. № 2.
В пространстве даны прямая а и точка М. Сколько существует прямых, проходящих через М и параллельных прямой а?
а) 0; б) 1; в) ; г) 0 или 1; д) 1 или .
Даны плоскость, и точка М. сколько существует прямых, проходящих через М и параллельных плоскости ?
А) 0; б) 1; в) ; г) 0 или ; д) 1 или .
Даны параллельные прямая а и плоскость . Сколько существует плоскостей, проходящих через а и параллельных ?
а) 0; б) 1; в) ; г) 0 или 1; д) 1 или .
В пространстве даны две параллельные прямые а и b. Сколько существует плоскостей, проходящих через прямую а и параллельных прямой b?
А) 0; б) 1; в) ; г) 0 или 1; д) 1 или .
Даны две пересекающиеся плоскости и и не лежащая на них точка М. Сколько существует прямых, проходящих через М и параллельных плоскостям и ?
А) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны две скрещивающиеся прямые а и b. Сколько существует пар параллельных плоскостей, одна из которых проходит через а, а другая – через b?
А) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
В пространстве даны две пересекающиеся прямые а и b и не лежащая на них точка М. Сколько существует плоскостей, проходящих через М и параллельных прямым а и b?
А) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Какие из следующих фигур можно получить как параллельную проекцию квадрата 2 дм 2 дм:
1 – прямоугольник 1 дм 2 дм,
2 –прямоугольник 2 дм 4 дм,
3- трапецию с основаниями 1 дм и 2 дм?
А) ни одну из этих фигур; б) только фигуру 1; в) фигуры 1 и 2; г) фигуры 2 и 3; д) все три фигуры.
Точки А и B и середина М отрезка АВ проектируется в точки А1 , В1 и М1 . Чему равна длина отрезка ММ1, если АА1 =3 см, ВВ1 =7 см?
а) 5 см; б) 4 см; в) 2 см; г) 5 см или 2 см.
В пространстве даны прямая а и точка М. Сколько существует плоскостей, проходящих через М и перпендикулярных прямой а?
а) 0; б) 1; в) ; г) 0 или 1; д) 1 или .
Даны плоскость и не лежащая в ней прямая а. Сколько существует плоскостей, проходящих через прямую а и перпендикулярных плоскости ?
а) 0; б)1; в) ; г) 0 или 1; д) 1 или .
Даны три параллельные плоскости , и . Расстояние между и равно 3 см, расстояние между и равно 5 см. Чему равно расстояние между плоскостями и ?
а) 2; б) 4; в) 8; г) 2 или 8; д) 4 или 8.
В пространстве даны три параллельные прямые a, b, c. Расстояние между прямыми a и b равно 2, расстояние между b и c равно 6. Чему равно расстояние x между прямыми a и c?
а) 0 х 6; б) 0 х 8; в) 2 х 8; г) 4 х 8; д) 4 х 6.
Известно, что прямая а параллельна прямой b, а прямая b пересекается с плоскостью . Каково взаимное расположение прямой а и плоскости ?
а) обязательно пересекаются; б) обязательно параллельны; в) могут и пересекаться, и быть параллельными.
Известно, что прямая а параллельна прямой b, а прямая b параллельна прямой c. Каково взаимное расположение прямых а и с?
а) обязательно параллельны; б) обязательно скрещиваются; в) параллельны или скрещиваются; г) параллельны, скрещиваются или пересекаются; д) параллельны или совпадают.
Известно, что прямая а параллельна прямой b, а прямая b параллельна плоскости . Каково взаимное расположение прямой а и плоскости ?
а) обязательно параллельны; б) обязательно пересекаются; в) параллельны или пересекаются; г) ответ отличен от (а) – (в).
Известно, что плоскость параллельна прямой b, а прямая b параллельна плоскости , отличной от . Каково взаимное расположение плоскостей и ?
а) обязательно параллельны; б) обязательно пересекаются; в) параллельны или пересекаются; г) ответ отличен от (а) – (в).
Даны три различные прямые a,b и c. Известно, что a скрещивается с b, а b скрещивается с прямой c. Каково взаимное расположение прямых a и c?
а) обязательно скрещиваются; б) скрещиваются или пересекаются; в) скрещиваются, пересекаются или параллельны; г) скрещиваются или параллельны; д) ответ отличен от указанных.
Даны две скрещивающиеся прямые а, b и не лежащая на них точка М. Сколько существует плоскостей, проходящих через М и параллельных прямым а и b?
а) 0; б) 1; в) 0 или 1; г) 0, 1 или 2; д) 0, 1 или .
Даны две скрещивающиеся прямые a и b. Сколько существует плоскостей, проходящих через прямую a и перпендикулярных прямой b?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны три попарно скрещивающиеся прямые a,b, c. Сколько существует прямых, пересекающих все эти три прямые?
а) 0; б) 1; в) ; г) 0 или ; д) 1 или .
На рёбрах AD, AB и CD тетраэдра ABCD произвольно взяты точки K, E, M. Какие рёбра, кроме трёх указанных, пересекают плоскость KEM?
а) АС; б) ВС; в) BD; г) никакие.
Какие из следующих фигур можно получить как параллельную проекцию куба:
1 – ромб (не квадрат);
2 – правильный пятиугольник;
3 – правильный шестиугольник?
а) только фигуру 1; б) фигуры 1 и 2; в) фигуры 2 и 3; г) фигуры 1 и 3;
д) все три фигуры.
2 вариант.
Сколько существует плоскостей, проходящих через три данные различные точки пространства?
а) 1; б) 0 или 1; в) ; г) 1 или ; д) 0, 1 или .
(2 -3).
Точки К, Е, М, Н – середины рёбер AB, BC, CD, DA тетраэдра ABCD
(рис. № 1).
Каково взаимное расположение прямых КМ и ЕН?
а) пересекаются; б) параллельны; в) скрещиваются; г) могут быть пересекающимися, параллельными и скрещивающимися (в зависимости от вида тетраэдра).
Каково взаимное расположение прямых АD и KM?
а) пересекаются; б) параллельны; в) скрещиваются; г) возможны все три случая.
(4) – (7).
Дан прямоугольный параллелепипед ABCDA1B1C1D1 (рис. №2).

Каково взаимное расположение прямых BD1 и A1C?
а) скрещиваются; б) пересекаются; в) параллельны; г) пересекаются или параллельны; д) определить нельзя.
Какие из прямых BC, CC1, A1D1 скрещиваются с прямой AA1?
а) только ВС; б) только СС1; в) только ВС и СС1; г) только ВС и A1D1; д) все три прямые ВС, СС1, А1D1.
Каково взаимное расположение прямой СВ1 и плоскости BDA1
а)параллельны; б) пересекаются; в) могут и пересекаться, и быть параллельными; г) ответ отличен от (а) –(в).
Каково взаимное расположение плоскостей AB1D1 и BCD?
а) параллельны; б) пересекаются; в) пересекаются или параллельны; г) ответ отличен от (а) – (в).
В пространстве даны прямая а и точка М. Сколько существует прямых, проходящих через М, пересекающих прямую а и перпендикулярных ей?
а) 0; б) 1; в) ; г) 0 или ; д) 1 или .
пространстве даны прямая а и точка М вне а. Сколько существует плоскостей, проходящих через М и параллельных прямой а?
а) 0; б) 1; в) ; г) 0 или ; д) 1 или .
Даны плоскость и точка М вне . Сколько существует плоскостей, проходящих через М и параллельных плоскости ?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны две скрещивающиеся прямые а и b. Сколько существует плоскостей, проходящих через а и параллельных b?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны две параллельные плоскости и , и не лежащая на них точка М. Сколько существует прямых, проходящих через М и параллельных плоскостям и ?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны плоскость и не лежащая в ней прямая а. Сколько существует плоскостей, проходящих через а и параллельных ?
а) 0; б) 1; в) ; г) 0 или 1; д) 1 или .
В пространстве даны две параллельные прямые a, b и не лежащая на них точка М. Сколько существует плоскостей, проходящих через М и параллельных прямым a и b?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Какие из следующих фигур можно получить как параллельную проекцию прямоугольника 1 дм 2 дм:
1 – квадрат 1 дм 1 дм,
2 – квадрат 2 дм 2 дм,
3 – прямоугольник 2 дм 3 дм?
а) ни одну из этих фигур; б) только фигуру 1; в) фигуры 1 и 2; г) фигуры 2 и 3; д) все три фигуры.
Точки А, В и середина М отрезка АВ проектируются в точки А1, В1 и М1. Чему равна длина отрезка ВВ1, если АА1= 3 см, ММ1= 2 см?
а)1 см; б) 5 см; в) 7 см; г) 1 см или 7 см; д) ответ отличен от указанных.
В пространстве даны плоскость и точка М. Сколько существует прямых, проходящих через М и перпендикулярных плоскости ?
а)0; б) 1; в) ; г) 0 или ; д) 1 или .
В пространстве даны плоскость и точка М. Сколько существует плоскостей, проходящих через М и перпендикулярных плоскости ?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны три параллельные плоскости , и .Расстояние между и равно 2, расстояние между и равно 6. Чему равно расстояние между плоскостями и ?
а) 2; б) 4; в) 8; г) 2 или 8; д) 4 или 8.
В пространстве даны три параллельные прямые a, b, c. Расстояние между a и b равно 3, расстояние между b и c равно 5. Чему равно расстояние х между прямыми а и с?
а) 0 х 5; б) 0 х 8; в)2 х 8; г) 3 х 8; д) 3 х 5.
Известно, что прямая а пересекает плоскость , а плоскость параллельна плоскости . Каково взаимное расположение прямой а и плоскости ?
а) обязательно пересекаются; б) обязательно параллельны; в) могут и
пересекаться, и быть параллельными; г) ответ отличен от (а) – (в).
Известно, что плоскость параллельна плоскости , а плоскость параллельна плоскости , отличной от . Каково взаимное расположение плоскостей и ?
а) обязательно параллельны; б) обязательно пересекаются; в) параллельны или пересекаются; г) ответ отличен от (а) – (в).
Известно, что прямая а параллельна плоскости , а плоскость параллельна прямой с, отличной от а. Каково взаимное расположение прямых а и с?
а) обязательно параллельны; б) обязательно скрещиваются; в) параллельны или скрещиваются; г) параллельны, скрещиваются или пересекаются; д) скрещиваются или пересекаются.
Известно, что плоскость параллельна плоскости , а плоскость параллельна прямой с, Каково взаимное расположение плоскости и прямой с?
а) обязательно параллельны; б) обязательно пересекаются; в) параллельны или пересекаются; г) ответ отличен от (а) – (в).
Даны три различные прямые a, b и c. Известно, что a параллельна b, а b пересекается с прямой c. Каково взаимное расположение прямых а и с?
а) обязательно скрещиваются; б) скрещиваются или пересекаются; в) скрещиваются, пересекаются или параллельны; г) скрещиваются или параллельны; д) ответ отличен от указанных.
В пространстве даны прямая а и две различные не лежащие на ней точки А и В. Сколько существует плоскостей, проходящих через А и В и параллельных прямой а?
а) 1; б) 0 или 1; в) 0, 1 или ; г) 0 или ; д) 1 или .
Даны две скрещивающиеся прямые a и b. Сколько существует пар взаимно перпендикулярных плоскостей, одна из которых проходит через а, а другая - через b? а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
Даны две скрещивающиеся прямые а и b и не лежащая на них точка М. Сколько существует прямых, проходящих через М и пересекающих прямые а и b?
а) 0; б) 1; в) ; г) 0 или 1; д) 0 или .
На рёбрах AD, DB и CD тетраэдра ABCD произвольно взяты точки K, E, M. Какие рёбра, кроме трёх указанных, пересекают плоскость KEM?
а) АВ; б) ВС; в) АС; г) никакие; д) определить нельзя.
Какие из следующих фигур можно получить как параллельную проекцию правильного тетраэдра:
1 – квадрат;
2 – трапецию;
3 – правильный шестиугольник?
а) ни одну из этих фигур; б) все три фигуры; в) только фигуру 1; г) только фигуру 2; д) фигуры 1 и 2.
2. Тема: «Тригонометрические формулы»
Цель: выработка умений и навыков применения тригонометрических формул.
Вариант № 1.
| Задания. | Ответы.
|
| 1. Запишите cos 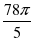 с помощью наименьшего положительного числа. с помощью наименьшего положительного числа. | 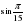  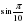
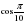
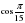 |
| 2. Найдите значения выражения 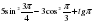 | 2,5 1,25 1,75 1,5 |
| 3. Упростите выражение 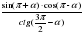 | 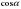 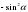  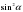 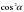 |
| 4. Упростите выражение 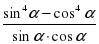 | 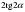 - 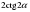 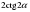 - 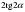 |
| 5. Найдите α, если cos 510 – cos 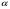 = 2 sin 170· sin 680 = 2 sin 170· sin 680 | 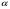 = 850 = 850 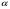 = -850 = -850
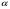 = 1360 = 1360 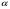 = 340 = 340 |
Вариант № 2.
| Задания. | Ответы.
|
| 1. Запишите sin  с помощью наименьшего положительного числа. с помощью наименьшего положительного числа. | - sin  sin  cos  - cos |
| 2. Найдите значения выражения  | 3,5 
 4,5 |
| 3. Упростите выражение  | cos2 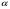 –sin 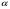 sin2 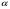 - cos 2 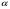 |
| 4. Упростите выражение  | tg 2 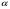 - ctg 2 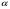 ctg 2 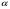 - tg 2 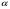 |
| 5. Найдите 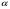 , если , если sin 280 – sin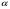 = - 2 sin 210· cos 490 = - 2 sin 210· cos 490 | 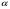 = 140 = 140
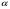 = 350 = 350 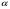 = -700 = -700 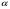 = 700 = 700 |
3. Тема: «Тригонометрические уравнения и неравенства
Цель: закрепление знаний студентов по данной теме и выявление «пробелов» в знаниях.
Решите уравнения: 1) 2 cos2  = 3 sin = 3 sin  , , 2) tg + ctg + ctg =2; =2; 3) cos 2 = 2 sin = 2 sin  + 1; + 1; 4) sin + sin 5 + sin 5 = 0; = 0; 5) 1 – 4 sin2 = 0. = 0. Ответы: 1) а.  = =  + 2n, n; + 2n, n; b.  = (-1)n = (-1)n  + n, n, + n, n, c.  = (-1)n +1 = (-1)n +1 + n, n, + n, n, d.  = (-1)n+1 = (-1)n+1  + n, n. + n, n. 2) a.  = =  + n, n, + n, n, b.  = =  + 2n, n, + 2n, n, c.  = + = + + n, n, + n, n, d.  = - = -  + n, n. + n, n. 3) Запишите сумму корней данного уравнения на промежутке [0; 2]. a) ; b) ; b)  ; c) 4,5; d) 2. ; c) 4,5; d) 2. 4) Найдите наименьший положительный корень уравнения. a)  ; b) ; b)  ; c) ; c)  ; d) ; d)  . . 5) Найдите сумму корней данного уравнения на промежутке [0; 2]. a)  ; b) 4; c) 2; d) ; b) 4; c) 2; d)  . . Решите неравенства: 1) 3 – 4 cos2  0; 0; 2)  . . Ответы: 1) a) ( -  +n; +n;  + n), n, + n), n, b) ( + n; + n;  + n), n, + n), n, c) ( + 2n; + 2n;  + 2n), n, + 2n), n, d) ( + 2n;  + 2n), n + 2n), n 2) a) (-2; 2), b) (-; -2) (2; ), c) , d) (-2; - ) ( ) ( ; 2). ; 2). | Решите уравнения: 1) 2 sin2  – 5 = -5 cos – 5 = -5 cos  ; ; 2) tg + ctg + ctg  = -2; = -2; 3) cos 2 = cos = cos  – 1; – 1; 4) cos  + cos 5 + cos 5 = 0; = 0; 5) 3 – 4cos2  = 0. = 0. Ответы: 1) a.  =n, n, =n, n, b.  = + 2n, n, = + 2n, n, c.  = =  + 2n, n, + 2n, n, d.  = 2 n, n. = 2 n, n. 2) a.  = = +n, n, +n, n, b.  = + = + + n, n, + n, n, c.  = - = -  + 2n, n, + 2n, n, d.  = - = - + n, n. + n, n.
3) Запишите сумму корней данного уравнения на промежутке [0; 2]. a) 2,5; b) 4 ; c) 2 ; d)  . . 4) Найдите наименьший положительный корень уравнения. a)  ; b) ; b)  ; c) ; c)  ; d). ; d). 5) Найдите сумму корней данного уравнения на промежутке [0; 3]. a) 4; b) 9; c) 6; d) 7,5. Решите неравенства: 1) 1 – 4 sin2  0; 0; 2)  0. 0. Ответы: 1) a) (- + 2n; + 2n;  + 2n), n, + 2n), n, b) ( + n; + n;  + n), n, + n), n, c) ( + n; + n;  + n), n, + n), n, d) (- + n; + n;  + n), n. + n), n. 2) a) (-3; 0), b) (0; 3), c) (-3; 0) (0; 3), d) (-3; 3). |
Решите уравнения: 1) 2 cos2  = 3 sin = 3 sin  , , 2) tg + ctg + ctg =2; =2; 3) cos 2 = 2 sin = 2 sin  + 1; + 1; 4) sin + sin 5 + sin 5 = 0; = 0; 5) 1 – 4 sin2 = 0. = 0. Ответы: 1) а.  = =  + 2n, n; + 2n, n; b.  = (-1)n = (-1)n  + n, n, + n, n, c.  = (-1)n +1 = (-1)n +1 + n, n, + n, n, d.  = (-1)n+1 = (-1)n+1  + n, n. + n, n. 2) a.  = =  + n, n, + n, n, b.  = =  + 2n, n, + 2n, n, c.  = + = + + n, n, + n, n, d.  = - = -  + n, n. + n, n. 3) Запишите сумму корней данного уравнения на промежутке [0; 2]. a) ; b) ; b)  ; c) 4,5; d) 2. ; c) 4,5; d) 2. 4) Найдите наименьший положительный корень уравнения. a)  ; b) ; b)  ; c) ; c)  ; d) ; d)  . . 5) Найдите сумму корней данного уравнения на промежутке [0; 2]. a)  ; b) 4; c) 2; d) ; b) 4; c) 2; d)  . . Решите неравенства: 1) 3 – 4 cos2  0; 0; 2)  . . Ответы: 1) a) ( -  +n; +n;  + n), n, + n), n, b) ( + n; + n;  + n), n, + n), n, c) ( + 2n; + 2n;  + 2n), n, + 2n), n, d) ( + 2n;  + 2n), n + 2n), n 2) a) (-2; 2), b) (-; -2) (2; ), c) , d) (-2; - ) ( ) ( ; 2). ; 2).
| Решите уравнения: 1) 2 sin2  – 5 = -5 cos – 5 = -5 cos  ; ; 2) tg + ctg + ctg  = -2; = -2; 3) cos 2 = cos = cos  – 1; – 1; 4) cos  + cos 5 + cos 5 = 0; = 0; 5) 3 – 4cos2  = 0. = 0. Ответы: 1) a.  =n, n, =n, n, b.  = + 2n, n, = + 2n, n, c.  = =  + 2n, n, + 2n, n, d.  = 2 n, n. = 2 n, n. 2) a.  = = +n, n, +n, n, b.  = + = + + n, n, + n, n, c.  = - = -  + 2n, n, + 2n, n, d.  = - = - + n, n. + n, n.
3) Запишите сумму корней данного уравнения на промежутке [0; 2]. a) 2,5; b) 4 ; c) 2 ; d)  . . 4) Найдите наименьший положительный корень уравнения. a)  ; b) ; b)  ; c) ; c)  ; d). ; d). 5) Найдите сумму корней данного уравнения на промежутке [0; 3]. a) 4; b) 9; c) 6; d) 7,5.
Решите неравенства: 1) 1 – 4 sin2  0; 0; 2)  0. 0. Ответы: 1) a) (- + 2n; + 2n;  + 2n), n, + 2n), n, b) ( + n; + n;  + n), n, + n), n, c) ( + n; + n;  + n), n, + n), n, d) (- + n; + n;  + n), n. + n), n. 2) a) (-3; 0), b) (0; 3), c) (-3; 0) (0; 3), d) (-3; 3). |
4. Тема: «Вычисление пределов функций».
Цель: проверка умений и навыков вычисления пределов функций.
1 вариант.
| Задание: вычислить пределы функций. | Ответы. |
| 1. а) lim (  ; ;  →3 →3
б) lim   →2 →2 | 1. а) 3; б)  2. а) -3; б) - . . 3. а) -3; б) . . 4. а) 9; б)  . . |
| 2.а) lim  ; ;  → 0 → 0
б) lim  . .  →3 →3 | 1. а)  ; б) 0. ; б) 0. 2. а)  ; б) 9. ; б) 9. 3. а)  ; б) 27. ; б) 27. 4. а)  ; б) 27. ; б) 27. |
| 3. а) lim  ; ; n→ ∞
б) lim  . . n→ ∞ | 1. а) 0; б) 2. 2. а)  ; б) 2. ; б) 2. 3. а) 0; б) 4. 4. а) 1; б) 3. |
2 вариант.
| Задание: вычислить пределы функций. | Ответы. |
| 1. а) lim ( 5 -3 –2);  →-4 →-4
б) lim   →2 →2 | 1. а) 1; б) . . 2. а) -23; б)  . . 3. а) 33; б) . . 4. а) -1; б)  . . |
| 2.а) lim  ; ;  → 0 → 0
б) lim   →2 →2
| 1. а) ; б) 4. ; б) 4. 2. а) - ; б) -4. ; б) -4. 3. а) - ; б) 0. ; б) 0. 4. а) - ; б) 4. ; б) 4. |
| 3. а) lim  ; ; n→ ∞
б) lim  n→ ∞
| 1. а) 0; б) 1. 2. а) 2; б) 1. 3. а) 0; б) 0. 4. а) -2; б) - 1. |
5. Тема: «Свойства функций»
Цель: проверка знаний студентов по применению основных свойств функций.
Вариант № 1.
| Задания. | Варианты ответов. |
| 1. Найдите область определения функции y=  . .
| [4; +∞) [-4; 4] (-∞; -4] U [4; +∞) (- ∞; 4] |
| 2. Найдите нули функции f( ) = ) =  | 0 -4; 4 
- |
| 3. Дана функция f( ) = ) =  3 – 2a 3 – 2a +5. Известно, что f(-1)=-3. Найдите f(-2). +5. Известно, что f(-1)=-3. Найдите f(-2). | 10 -12 -17 -5 |
| 4. Найдите область значений функции у = -  | [- ; +∞) ; +∞) (-∞; -  ] ] (- ∞; - ] ] [ ; +∞) ; +∞) |
Вариант № 2.
| Задания. | Варианты ответов. |
| 1. Найдите область определения функции y= 
| [4; +∞) [1 ; 12] [-12; 0] [- ; ; ] ] |
| 2. Найдите нули функции f( ) = ) =  | 0; 2,45 
-  ; ;  |
| 3. Дана функция f ( ) =- ) =-  3 – 4a 3 – 4a -3. Известно, что f(-2)=1. Найдите f(-1). -3. Известно, что f(-2)=1. Найдите f(-1). | 2 -8 -4 -2 |
| 4. Найдите область значений функции у =  | [-1,5; +∞) (-∞; 1,25 ] (- ∞; -1,5 ] [-3,25; +∞) |
6. Тема: «Техника дифференцирования»
Цель: выработка умений и навыков студентов по применению основных формул дифференцирования, а также, выявление «пробелов» в знаниях.
Вариант № 1.
| Задания. | Варианты ответов. |
| 1. Найдите производную функции f ( ) = ) = и вычислите её значение при и вычислите её значение при  = -1. = -1. | -2,5 2,5 -1,5 1,5 |
| 2. Найдите производную функции g ( ) = ) =  | -   -   |
| 3. Найдите f '(0,5), если f ( ) = ) =  . . | 3 
 2 |
| 4. Для функции f ( ) = 3 sin2 ) = 3 sin2  вычислите f '(- вычислите f '(-  ). ). | -3 6 -1,5 0,5 |
Вариант № 2.
| Задания. | Варианты ответов. |
| 1. Найдите производную функции f ( ) = - ) = -  и вычислите её значение при и вычислите её значение при  = -2. = -2. | -3 2 -5 3 |
| 2. Найдите производную функции g ( ) = ) =  |   - - |
| 3. Найдите f ' (- 0,5), если f ( ) = ) =  | -0,5 4 -2 0,5 |
| 4. Для функции f ( ) = 5 cos2 ) = 5 cos2  вычислите f '(- вычислите f '(- ) ) | 5 10 -5 -10 |
7. Тема: «Исследование функций с помощью производной»
Цель: закрепление знаний по исследованию функций с помощью производной.
Вариант № 1.
| Задания. | Варианты ответов. |
| 1. Дана функция f ( ) = - ) = -  . Найдите её критические точки. . Найдите её критические точки. | а)  =2; =2;  =-1 =-1 б)  = 1; = 1;  =-2 =-2 в)  =-3; =-3;  = 1 = 1 г)  =-2; =-2;  =3 =3 |
| 2. Найдите точки экстремума функции f ( ) = ) =  . . | а)  max = 3, max = 3,  min =0 min =0 б)  min =3, min =3,  max = 0 max = 0 в)  min =3 min =3 г) Ø |
| 3. Найдите промежутки убывания функции f ( ) = ) =  . . | а) [-4; 0] б) (- ∞; 0]; [4; +∞) в) [0; 4] г) Ø |
| 4. Найдите экстремумы функции f ( ) = ) =  . . | а)  = 2 = 2 б)  =1,5 =1,5 в)  = = г)  = = |
Вариант № 2.
| Задания. | Варианты ответов. |
| 1. Дана функция f ( ) = ) =  - . Найдите её критические точки. - . Найдите её критические точки. | а)  = -1; = -1;  = 3 = 3 б)  =-2; =-2;  =1,5 =1,5 в)  =-1,5; =-1,5;  = 2 = 2 г)  =0,5; =0,5;  =2 =2 |
| 2. Найдите точки экстремума функции f ( ) = ) =  . . | а)  max = -1,5, max = -1,5,  min =0 min =0 б)  min = -1, 5, min = -1, 5,  max = 0 max = 0 в)  min =-1,5 min =-1,5 г)  max = 1,5 max = 1,5 |
| 3. Найдите промежутки возрастания функции f ( ) = ) =  . . | а) [-6; 0] б) (- ∞; -6]; [0; +∞) в) [0; 6] г) (- ∞; 0]; [6; +∞) |
| 4. Найдите экстремумы функции f ( ) = ) =  | а)  б) 2 в) 4 г) 8 |
8. Тема: « Первообразная»
Цель: выработка умений находить первообразную функции и выявление «пробелов» в знаниях студентов.
1 вариант.
| Задания. | Варианты ответов. |
| 1. Найдите общий вид первообразных F( ) для функции ) для функции f ( )= )=  . . | а) F( ) = ) =  б) F( ) = ) =  в) F( ) = ) =  г) F( ) = ) =  |
| 2. Известно, что f( ) = ) =  и F(-2)=5 . Найдите F(-1). и F(-2)=5 . Найдите F(-1). | а) -8, 25 б) 10,75 в) -10,25 г) 7,75 |
2 вариант.
| Задания. | Варианты ответов. |
| 1. Найдите общий вид первообразных F( ) для функции ) для функции f ( )= )=  . . | а) F( ) = ) =  б) F( ) = ) =  в) F( ) = ) =  г) F( ) = ) =  |
| 2. Известно, что f( ) = ) = и F(-1) = 3. Найдите F(-2). и F(-1) = 3. Найдите F(-2). | а) -23 б) -18 в) -27 г) -15 |
9. Тема: «Определённый интеграл»
Цель: выработка умений и навыков применения основных формул интегрирования.
1 вариант.
| Задания. | Варианты ответов. |
| 1. Вычислите:  . . | а) 27 б) 24 в) 18 г) 21 |
| 2. Вычислите: . . | а) 1,5 б)  в) -  |
| 3. Вычислите:  . . | а) -2 б) 2 в) -3 г) 3 |
2 вариант.
| Задания. | Варианты ответов. |
| 1. Вычислите:  . . | а)  б)  в)  г)  |
| 2. Вычислите:  | а) 0 б) -12 в) 12 |
| 3. Вычислите:  . . | а) -3,5 б) 4,5 в) -4,5 г) 3,5
|
10. Тема: « Определение логарифма»
Цель: выработка навыков вычисления логарифмов.
1 вариант.
| Задания. | Варианты ответов. |
| 1. Найдите значения выражения: log 125 5 – log √2  + log 2,5 0,4. + log 2,5 0,4.
| а) -3,5 б) 4,5 в)  г) -  |
| 2. Вычислите: 9 log36 – 1,5 . | а) 2,5 б)  в) 1,5 г)  |
| 3. Решите уравнения log4  =-1,5 и log =-1,5 и log   = - = -  . Запишите произведение их корней. . Запишите произведение их корней. | а)  б)  в)  г)  |
2 вариант.
| Задания. | Варианты ответов. |
| 1. Найдите значения выражения: log 64 4 + log √3  - log 0,2 5. - log 0,2 5.
| а) -  б)  в) -  г) -  |
| 2. Вычислите: 41,5 – log 16 25. | а) 2,5 б) 2,6 в) 1,5 г) 1,6 |
| 3. Решите уравнения log8  = - = -  и log и log 0,2 = - 0,2 = -  . Запишите произведение их корней. . Запишите произведение их корней. | а) 4,2 б) 25,25 в) 6,25 г) 0,8 |
11. Тема: «Показательная функция»
Цель: отработка умений и навыков: 1) применения свойств показательной функции; и 2) решения простейших показательных уравнений и неравенств.
1 вариант.
| Задания. | Варианты ответов. |
| 1. График функции у = а  проходит через точку М (1; 3). проходит через точку М (1; 3). а) Найдите основание а. б) Сравните а 0,37 и а 0,38. в) Сравните числа а -0,01 и 1. | 1. а) 3; б) а 0,37 а 0,38; в) а -0,01 2. а)  ; б) а 0,37 0,38; ; б) а 0,37 0,38; в) а -0,01 1 3. а) 3; б) а 0,37 а 0,38; в) а -0,01 1 4. а)  ; б) а 0,37 0,38; ; б) а 0,37 0,38; в) а -0,01 |
| 2. Решите неравенства: а) (  ) ) б) 2,3 1. 1. | 1. а) (0; + ∞); б) (0; +∞) 2. а) (-∞; 0); б) (0; +∞) 3. а) (0; +∞); б) (-∞; 0) 4. а) (-∞; 0); б) (-∞; 0) |
| 3. Решите уравнение: 2  +2 – 2 +2 – 2 -1 = 28. -1 = 28. | 1. 3 2. 3,5 3. 4 4. -3 |
2 вариант.
| Задания. | Варианты ответов. |
| 1. График функции у = а  проходит через точку А (2; проходит через точку А (2;  ). ). а) Найдите основание а. б) Сравните а 1,5 и а 1,3. в) Сравните числа а -0,3 и 1. | 1. а)  ; б) а 1,5 а 1,3; ; б) а 1,5 а 1,3; в) а -0,3 1 2. а)  ; б) а 1,5 1,3; ; б) а 1,5 1,3; в) а -0,3 3. а)  ; б) а 1,5 1,3; ; б) а 1,5 1,3; в) а -0,3 1 4. а)  ; б) а 1,5 а 1,3; ; б) а 1,5 а 1,3; в) а -0,3 |
| 2. Решите неравенства: а) 0,6  б) 3,5  1. 1. | 1. а) (-∞; 0); б) (0; +∞) 2. а) (0; + ∞); б) (0; +∞) 3. а) (0; +∞); б) (-∞; 0) 4. а) (-∞; 0); б) (-∞; 0) |
| 3. Решите уравнение: 5  +1 + 5 +1 + 5  -1 + 5 -1 + 5  = 155. = 155. | 1. 3 2. 2 3. 5 4. -2 |
12. Итоговые тесты
Вариант 1.
Блок А.
| № п/п | Задание (вопрос)
| Эталон ответа |
| Инструкция по выполнению заданий № 1 -4: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв. Например, |
|
| № задания. | Вариант ответа. |
|
| 1 | 1 –В, 2- А, 3 -Б |
| 1. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Погрешность приближения. 2. Абсолютная погрешность. 3. Относительная погрешность.
| Столбец 2. А. Модуль разности точного и приближенного значений Б. Отношение абсолютной погрешности к модулю приближённого значения. В. Абсолютная погрешность приближённого значения а не превышает Δ а. Г. Разность точного и приближённого значений. |
|
| 2. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Функция. 2. Множество значений функции. 3. Область определения функции.
| Столбец 2. А. Множество всех действительных значений функции у. Б. Если каждому допустимому значению  соответствует определённое значение у. соответствует определённое значение у. В. Числовое значение функции, соответствующее данному числовому значению аргумента. Г. Множество всех действительных значений аргумента.
|
|
| 3. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Степенная функция. 2. Показательная функция. 3. Тригонометрическая функция.
| Столбец 2. А. у = а , где а 0. , где а 0. Б. у = tg . . В. у = k  + b. + b. Г. у =  k , где k – произвольное действитель- k , где k – произвольное действитель- ное число. | |
| 4. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Синус числа α. 2. Косинус числа α. 3. Тангенс числа α.
| Столбец 2. А. Абсцисса точки единичной окружности, соответствующая числу α. Б. Отношение косинуса этого числа к его синусу. В. Ордината точки единичной окружности, соответствующая числу α. Г. Отношение синуса этого числа к его косинусу. |
|
| Инструкция по выполнению заданий № 5 – 23: выберите букву, соответствующую правильному варианту ответа и запишите её в бланк ответов. |
| 5. | Представьте в виде десятичной дроби  . . А. 0, 0(013) Б. 0, (13) В. 0, (013) Г. 0, 0(13) | |
| 6. | Представьте периодическую десятичную дробь 0, (3) в виде обыкновенной: А.  Б.  В.  Г.  | |
| 7. | Вычислите: log6 2 + log6 3. А. 5 Б. 0 В. 1 Г. 6 |
|
| 8. | Решите уравнение: 32 = 81. = 81. А. 13,5 Б. 1 В. 2 Г. 4 |
|
| 9. | Вычислите: arcsin (-1): А. 0. Б.  . . В. –  . . Г. π. |
|
| 10. | Найдите корень уравнения cos t = -  на промежутке [- π; 0 ]. на промежутке [- π; 0 ]. А. –  Б. -  В. –  Г. корней нет |
|
| 11.
| Дана функция f ( ) = – 2а ) = – 2а + 5. Известно, что f (-1) = -3. + 5. Известно, что f (-1) = -3. Найдите f (-2). А. 10 Б. -12 В. -17 Г. -5 |
|
| 12.
| Вычислите lim ( 2 -5 2 -5 +3): +3):  → 3 → 3 А. 3 Б. -3 В. 9 Г. -6 |
|
| 13.
| Найдите производную функции у =5  4 – 8 4 – 8 . . А. у '=20  3 -8 3 -8 Б. у '=5  3 -8 3 -8 В. у '=20 3 -8 3 -8 Г. у '=4 3 -8 3 -8 | |
| 14. | Найдите промежутки убывания функции у =  3 – 6 3 – 6 2 +5. 2 +5. А. [-4; 0] Б. (0; 4) В. (- ∞; 0); (4; +∞) Г. Ø |
|
| 15. | Дана функция f ( ) = ) =  3 – 12 3 – 12 . Найдите её критические точки. . Найдите её критические точки. А. 2 Б. -2 В. -2; 2 Г. 0 |
|
| 16. | Исследуйте функцию на экстремум f ( ) = ) =  2 + 4 2 + 4 . . А.  min =2 min =2 Б.  max =-2 max =-2 В.  min =-2 min =-2 Г. Ø |
|
| 17.
| Найдите общий вид первообразных F ( ) для функции f ( ) для функции f ( ) = ) =  3 – 5 3 – 5 2 +2. 2 +2. А. F ( )= )=  Б. F( )= )=  В. F( )= )=  Г. F( )= )=  |
|
| 18. | Вычислите:  А. 6 Б. -3 В. -4 Г. -6 |
|
| 19.
| Даны векторы а (7; 2; -1), b (-4; 3; 1). Найдите координаты вектора 2 + +  : : А. (1; 8; 2). Б. (10; 7; -1). В. (10; 7; 1). Г. (3; 5; 0). |
|
| 20. | Даны параллельные прямая а и плоскость α. Сколько существует плоскостей, проходящих через а и параллельных α? А. 0. Б. 0 или 1. В. ∞ Г. 1. |
|
| 21. | В пространстве даны прямая а и точка М. Сколько существует плоскостей, проходящих через М и перпендикулярных прямой а? А. 0 Б. 1. В. 0 или 1. Г. ∞ |
|
| 22. | Даны три попарно скрещивающиеся прямые a, b, c. Сколько существует прямых, пересекающих все эти прямые? А. 1. Б. 0. В. ∞. Г. 1 или ∞. |
|
| 23. | Найдите число размещений из 10 элементов по 4, т.е. А4 10 : А. 40 Б. 504 В. 5040 Г. 30240 |
|
Блок Б.
| № п/п | Задание (вопрос) | Эталон ответа |
| Инструкция по выполнению заданий № 24- 35: в соответствующую строку бланка ответов запишите краткий ответ на вопрос, окончание предложения или пропущенные слова. |
| 24. | Если каждому допустимому значению  соответствует определённое значение у, то у называется……. соответствует определённое значение у, то у называется……. |
|
| 25. | Функция у= f ( ) называется чётной, если выполняется равенство f (- ) называется чётной, если выполняется равенство f (- ) =…… ) =…… | |
| 26. | График чётной функции симметричен относительно оси…. |
|
| 27. | Функция называется возрастающей в некотором промежутке (а; b) , если для любых  1 и 1 и  2, принадлежащих этому промежутку, при 2, принадлежащих этому промежутку, при  1 2 выполняется неравенство 1 2 выполняется неравенство f ( 1)….f ( 1)….f ( 2). 2). |
|
| 28. | Закончите формулу: основное тригонометрическое тождество sin2 α+ cos2 α =…. |
|
| 29. | Предел отношения приращения функции Δ у к приращению аргумента Δ при Δ при Δ  → 0 называется ….. функции. → 0 называется ….. функции. |
|
| 30. | Если при переходе через критическую точку производная меняет свой знак, то в этой точке будет экстремум, причём …..если производная меняет знак с «+» на «-« |
|
| 31. | Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной точки, называется….. |
|
| 32. | Две плоскости называются параллельными, если они ….. |
|
| 33. | Конус можно представить как тело, полученное вращением ……. …… вокруг одного из его катетов. |
|
| 34. | Что изучает предмет «Теория вероятностей»? |
|
| 35. | Тело, граница которого есть объединение конечного числа многоугольников, называется……….. |
|
Вариант 2.
Блок А.
| № п/п | Задание (вопрос)
| Эталон ответа |
| Инструкция по выполнению заданий № 1-4: соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв. Например, |
|
| № задания. | Вариант ответа. |
|
| 1 | 1 –В, 2- А, 3 -Б |
| 1. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Точка максимума. 2. Точка минимума. 3. Экстремум функции.
| Столбец 2. А. Точки максимума и точки минимума. Б. Если для все  , таких, что , таких, что  ≠ ≠  0 из некоторой окрестности точки х0 выполняется неравенство f ( 0 из некоторой окрестности точки х0 выполняется неравенство f ( ) f ( ) f ( 0). 0). В. Точки, в которых производная равна нулю или не существует. Г. Если для все  , таких, что , таких, что  ≠ ≠ 0 из некоторой окрестности точки х0 выполняется неравенство f ( 0 из некоторой окрестности точки х0 выполняется неравенство f ( ) f ( ) f ( 0). 0).
|
|
| 2. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Производная. 2. Физический смысл производной. 3. Геометрический смысл производной.
| Столбец 2. А. Производная функции у = f ( ) в некоторой точке равна угловому коэффициенту касательной, проведённой к графику функции ) в некоторой точке равна угловому коэффициенту касательной, проведённой к графику функции у = f ( ) в этой точке. ) в этой точке. Б. Предел отношения приращения функции Δ у к приращению аргумента Δ при Δ → 0. при Δ → 0. В. Приращение ординаты касательной, проведённой к графику этой функции в точке ( 0; f ( 0; f ( 0)), соответствующему приращению её абсциссы 0)), соответствующему приращению её абсциссы  0 на Δ 0 на Δ . . Г. Скорость прямолинейного движения тела в любой момент времени t есть производная от пути s по времени t. |
|
| 3. | Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Первообразная. 2. Неопределённый интеграл. 3. Определённый интеграл.
| Столбец 2. А. Множество всех первообразных F( ) + С, где С=const. ) + С, где С=const. Б. Приращение F(b) – F(a) любой из первообразных функций F ( ) + С при изменение аргумента от ) + С при изменение аргумента от  =а до =а до  = b. = b. В. Функция, восстанавливаемая по данной производной. Г. Главная часть у'Δ приращения функции f( приращения функции f( ). ). |
|
| 4
| Установите соответствие между терминами и их содержанием. |
| Столбец 1. 1. Пересекающиеся прямые. 2. Параллельные прямые. 3. Скрещивающиеся прямые. | Столбец 2. А. Прямые не пересекаются и не параллельны. Б. Прямые лежат в одной плоскости и не пересекаются. В. Прямые лежат в плоскости и имеют общую точку. Г. Прямые пересекаются под прямым углом. |
|
| Инструкция по выполнению заданий № 5 – 23: выберите букву, соответствующую правильному варианту ответа и запишите её в бланк ответов. |
| 5. | Представьте в виде десятичной дроби  . . А. 0,1 (27) Б. 0, (127) В. 0, 127 Г. 0, 12(7) |
|
| 6. | Представьте периодическую десятичную дробь 0,2(5) в виде обыкновенной: А.  Б.  В.  Г.  |
|
| 7. | Вычислите: log6 2 – log6  А. 15 Б. 1 В. 3 Г. 6 |
|
| 8. | Решите уравнение: 4 3 = 64. = 64. А.  Б.  В. 1 Г. 16 |
|
| 9. | Вычислите: arcsin (-  ). ). А. 1 Б. –  В. -π Г.  |
|
| 10. | Найдите корень уравнения cos t = -  на промежутке [- π;0 ]. на промежутке [- π;0 ]. А. –  Б. -  В. –  Г. корней нет |
|
| 11.
| Дана функция f ( ) = - ) = -  3 – 4а 3 – 4а -3. Известно, что f (-2) = 1. Найдите f (-1). -3. Известно, что f (-2) = 1. Найдите f (-1). А. 2 Б. -8 В. -4 Г. -2 |
|
| 12.
| Вычислите lim (5+ 2 + 2 ) + 2 )  →- 3 →- 3 А. -11 Б. 8 В. 20 Г. 2 |
|
| 13. | Найдите производную функции у =3  7 – 12 7 – 12  . . А. у '=3(7 6 -4 6 -4  ) ) Б. у '=3(7 6 -4) 6 -4) В. у '=12 -21 6 6 Г. у '=21 6 +4 6 +4 | |
| 14. | Найдите промежутки возрастания функции у =  3 + 9 3 + 9 2 -4 2 -4 А. [-6; 0] Б. [0; 6] В.(- ∞; -6]; [0; +∞) Г.(- ∞; -0]; [6; +∞) | |
| 15. | Дана функция f ( ) = ) =  3 – 3 3 – 3 . Найдите её критические точки. . Найдите её критические точки. А. -1 Б. 0; 1 В. -1; 1 Г. -1; 0 |
|
| 16. | Исследуйте функцию на экстремум: f ( ) = 2 ) = 2 2 – 2 –  +5. +5. А.  min =4 min =4 Б.  max = max =  В.  min = min =  Г. Ø |
|
| 17. | Найдите общий вид первообразных F ( ) для функции f ( ) для функции f ( ) = ) =  2 – 4 2 – 4 + 7. + 7. А. F( )= )=  2 – 2 –  + 7 + 7 +С +С Б. F( )= )=  В. F( )= )=  Г. F( )= )=  |
|
| 18. | Вычислите:  А. 2 Б.  В. 1 Г. -  |
|
| 19. | Даны векторы а (6; 3; -2), b (-5; 2; 0). Найдите координаты вектора  – 2 – 2 . . А. (16; 7; 2) Б. (11; -1; -2) В. (16; -1; -2). Г. (-4; 7; -2) | |
| 20. | Известно, что плоскость α параллельна плоскости β, а плоскость β параллельна плоскости γ, отличной от α. Каково взаимное расположение плоскостей αи γ ? А. Обязательно параллельны. Б. Обязательно пересекаются. В. Параллельны или пересекаются. Г. Ответ отличен от (А) – (В). |
|
| 21. | Даны две пересекающиеся плоскости α и β и не лежащая на них точка М. Сколько существует прямых, проходящих через М и параллельных плоскостям α и β ? А. 0 Б. 1 В. 0 или 1 Г. ∞ |
|
| 22. | Даны две скрещивающиеся прямые а и b. Сколько существует плоскостей, проходящих через прямую а и перпендикулярных прямой b? А. 0. Б. 1. В. 0 или 1. Г. ∞. |
|
| 23. | Вычислите значение выражения С46 + С05: А. 15 Б. 24 В. 15 Г. 16. |
|
Блок Б.
| № п/п | Задание (вопрос) | Эталон ответа |
| Инструкция по выполнению заданий № 24 - 35: в соответствующую строку бланка ответов запишите краткий ответ на вопрос, окончание предложения или пропущенные слова. |
| 24. | Множество всех действительных значений аргумента, при которых функция может иметь действительные значения называется.. |
|
| 25. | Функция у = f ( ) называется нечётной, если выполняется равенство f (- ) называется нечётной, если выполняется равенство f (- ) = …. ) = …. |
|
| 26. | График нечётной функции симметричен относительно…. |
|
| 27. | Функция называется убывающей й в некотором промежутке (а; b) , если для любых  1 и 1 и  2, принадлежащих этому промежутку, при 2, принадлежащих этому промежутку, при  1 2 выполняется неравенство f ( 1 2 выполняется неравенство f ( 1)….f ( 1)….f ( 2). 2). |
|
| 28. | Десятичным логарифмом числа называется логарифм по основанию…. |
|
| 29. | Закончите формулу: tg α · ctg α = ….. |
|
| 30. | Если при переходе через критическую точку производная меняет свой знак, то в этой точке будет экстремум, причём …..если производная меняет знак с «-» на «+«. |
|
| 31. | Запишите формулу Ньютона – Лейбница. |
|
| 32. | Запишите формулу по которой находятся перестановки из n элементов. |
|
| 33. | Прямая и плоскость называются параллельными, если они …….. |
|
| 34. | Цилиндр можно представить как тело, полученное вращением ……. вокруг одной из его сторон. |
|
| 35. | Фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой, называется………. |
|
13. Тест по теме: «Основные элементы комбинаторики»
Цель: закрепление знаний студентов по основным формулам комбинаторики.
Соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения называются…
размещения
сочетания
перестановки.
2. Записать формулу для числа размещений из n элементов по m.
a. 
b. 
c. 
3. Соединения, которые отличаются, друг от друга хотя бы одним элементом называются…..
размещения
сочетания
перестановки.
4. Записать формулу для числа сочетаний из n элементов по m .
a. 
b. 
c. 
Вероятность P находится по формуле:
a. 
b. 1- 
c. 
6. Вычислить 5! + 6!:
a. 11!
b. 840
7. Достоверному событию соответствует вероятность
a. P (A) =0
b. P (A) = -1
c. P (A) = 1
8. Вычислить: 
a. 1,04 !
b. 2652
5. Заключение
В методической разработке показано применение тестов на уроках математики, описана методика создания тестов, их достоинства, а также, обобщён опыт работы. Мне, кажется, что цели, поставленные при написании данной разработки были достигнуты: во – первых, раскрыты достоинства тестов – как одного из методов контроля знаний; во – вторых, даны рекомендации другим преподавателям по составлению тестов; в – третьих, приложены тесты, составленные на протяжении нескольких лет и успешно, применяемые на уроках математики; и, в – четвёртых, мои личные знания были расширены по данному вопросу, в связи с изучением большого количества литературы.
1� Столяр А.А. «Практикум по педагогике математики», - Мн., 1978.

 Получите свидетельство
Получите свидетельство Вход
Вход



 рис. №1.
рис. №1. рис. № 2.
рис. № 2.
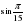
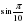
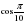
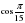
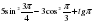
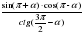
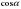
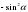
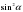
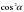
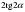
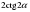
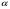 = 2 sin 170· sin 680
= 2 sin 170· sin 680








 Материал для учителя математики "Тестирование - как один из методов контроля знаний" (0.59 MB)
Материал для учителя математики "Тестирование - как один из методов контроля знаний" (0.59 MB)
 0
0 1251
1251 30
30 Нравится
0
Нравится
0


