Росрыболовство
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Астраханский государственный технический университет»
Обособленное структурное подразделение «Волго-Каспийский морской рыбопромышленный колледж» федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Астраханский государственный технический университет»
Семинар
«Математические методы в исследовательской работе»
Автор: Земцов Д.В.,
преподаватель математики ФГБОУ ВПО «АГТУ» ОСП «ВКМРПК»
Астрахань, 2013
Цели мероприятия:
- развитие интереса к методам математической статистики как средству проверки гипотезы и обработки результатов исследования;
- формирование умений вычислять основные числовые характеристики выборки, доказывать или опровергать гипотезу исследования с помощью таких методов, как критерий Стъюдента и χ² - критерий;
- развитие информационной и коммуникативной компетентности.
Материальное обеспечение:
Интерактивная доска (23 слайда презентации SMART Notebook), компьютер, проектор, научные калькуляторы (15 шт.), сигнальные карточки (60 шт), раздаточный материал (30 листов), цифровой фотоаппарат, призы.
Сценарий мероприятия
Вступительная речь преподавателя. «Как известно, всякое знание в начале своего пути проходит стадию версий и гипотез. Вы – студенты экономического отделения, а экономика, как и естествознание, и психология – дисциплина точная. В точных науках эти версии и гипотезы проверяются экспериментальным путем, а также, с помощью математической статистики. Именно этому разделу математики посвящен наш сегодняшний семинар «Математические методы в исследовательской работе», цель которого – познакомиться с методами первичной и вторичной обработки числовых данных, полученных в результате исследования (наблюдения, эксперимента, опроса, тестирования, различных измерений, проб и т.д.). В частности, вторичные методы применяются для проверки (то есть доказательства или опровержения) гипотез. Например, у меня есть гипотеза: группа ЭБ-11 в первом семестре в целом показала существенную положительную динамику в изучении математики по сравнению с результатами среза школьных знаний в сентябре. Но так ли это? Это можно проверить с помощью специальных статистических формул и расчетов по ним».
Вопрос 1: Первичная обработка статистических данных.
Докладчики: студенты группы ЭБ-11 Суханова А., Жижимова К.
Математическая статистика – это раздел математики, задачей которого является создание методов сбора и обработки статистических данных для получения обоснованных научных и практических выводов о закономерностях окружающего мира. Предметом математической статистики является изучение методов сбора, систематизации, обработки и использования статистических данных для проверки экспериментальных гипотез, получения научно обоснованных выводов и принятия решений. При этом под статистическими данными понимается совокупность чисел, которые являются количественными характеристиками интересующих нас признаков изучаемых объектов.
Пожалуйста, прочитайте текст на интерактивной доске, и скажите, как вы это поняли, может быть, приведите примеры. Как вы понимаете слово «гипотеза»?
Математическая статистика зародилась в 18 веке в работах Я. Бернулли, П. Лапласа. В наши дни математическая статистика продолжает интенсивно развиваться; расширяется круг ее задач и методов исследования с широким применением компьютерной техники.
Статистические данные собираются в результате научного или практического исследования, например, лабораторного эксперимента, пробы, опыта, социологического опроса, психологического тестирования, экспертного наблюдения. Например, с целью определения качества электрических лампочек, выпускаемых заводом, отмечают, сколько часов горит каждая из выбранных энергосберегающих лампочек до выхода из строя (смотрите слайд):
3800, 2100, 4580, 5300, 3300, 2990, 4000, 4000, 3860, 4560.
Полученная совокупность чисел – это и есть статистические данные.
Прежде всего следует различать понятия «генеральная совокупность» и «выборочная совокупность». Например, требуется количественно оценить некоторые особенности характера студентов нашего колледжа. В колледже учится несколько сотен студентов, и на сплошное исследование ушло бы немало времени, то есть сплошное исследование нецелесообразно. Или, если исследуется качество электрических лампочек, то бессмысленно исследовать на срок горения все лампочки данной партии, так как в результате вся партия уничтожилась бы. В таких случаях из всей генеральной совокупности объектов выбирают некоторое разумное число объектов, достаточное для того, чтобы сделать достоверные выводы. Такие объекты составляют выборочную совокупность, или просто выборку. Сразу заметим, что число объектов данной выборки называют объемом выборки.
Пример. Цех выпустил 2000 деталей. Для проверки качества отобраны 20 случайных деталей.
Тогда объем генеральной совокупности равен N=2000, а объем выборочной совокупности (выборки) составляет n=20 деталей.
Обработка статистических данных начинается с группировки этих чисел в порядке неубывающего значения свойства, в результате чего получается упорядоченный статистический ряд.
Например, перед семинаром мы провели шуточный социологический опрос десяти человек: сколько «валентинок» вы получили сегодня, в День Влюбленных?
На слайде вы видите исходный ряд. Составим упорядоченный выборочный ряд (на доске располагает значения в неубывающем порядке).
Размах выборки – это разность между наибольшим и наименьшим значением (на доске находит размах выборки).
Медиана – это значение, занимающее середину упорядоченного ряда, а в случае четного количества равное среднему арифметическому двух средних значений ряда (на доске находит медиану выборки).
Статистическое распределение – это таблица, в первой строке которой записаны все различные значения выборки в порядке возрастания, а во второй строке указаны соответствующие им частоты (на доске заполняет таблицу статистического распределения выборки).
Мода – это значение признака выборки, имеющее наибольшую частоту (на доске находит моду выборки).
Все запомнили? Теперь рассмотрим числовые характеристики выборки.
1) Выборочная средняя – это среднее арифметическое значение признака выборки. И потому, она вычисляется как сумма всех значений, деленная на их количество, что можно выразить формулой, которую вы видите на доске:
Вычислим выборочную среднюю в нашем опросе. Для этого перемножаем значения с их частотами и такие произведения складываем (проводит вычисления на доске).
2) Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений признака выборки от выборочной средней. Сокращенная формула перед вами на доске:
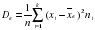
Вычислим выборочную дисперсию в нашем опросе. Для этого из значений выборки вычитаем среднюю, возводим такие разности в квадрат, умножаем на частоты и такие произведения складываем (проводит вычисления на доске).
3) Выборочное среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии, формула перед вами на доске.
Следует отметить, что выборочное отклонение означает, насколько в среднем значения признака выборки отличаются от выборочной средней (вычисляет на доске с помощью калькулятора).
Теперь мы предлагаем вам решить задачу, чтобы закрепить основные понятия и формулы математической статистики. Для этого возьмите раздаточный материал с задачей № 1.
Задача 1. Даны результаты обучения в 1 семестре иностранному языку в первой подгруппе ЭБ-11 (для удобства ваших вычислений мы сократили численность подгрупп до n = 10 человек):
3; 4; 4; 4; 4; 3; 4; 5; 4; 3.
a) составьте упорядоченный ряд и найдите размах выборки и медиану;
b) составьте статистическое распределение частот и по нему определите моду и вычислите выборочную среднюю, дисперсию и среднее квадратическое отклонение.
Далее – идет работа по заполнению раздаточных таблиц № 1.
Составьте упорядоченный ряд (как вы помните, надо расположить значения в неубывающем порядке).
Найдите размах выборки (разность между наибольшим и наименьшим значением).
Найдите медиану – середину упорядоченного ряда.
Составьте статистическое распределение выборки в виде таблицы. Назовите первую строку – значения выборки. Назовите вторую строку – частоты значений.
Найдите моду выборки – значение с наибольшей частотой.
Проверим результаты (один обучающийся называет свои результаты, остальные голосуют сигнальными карточками: зеленая – верно; красная - неверно).
Теперь вычислим числовые характеристики выборки.
Найдите выборочную среднюю, то есть среднее арифметическое значение. Что у вас получилось?
Теперь вычислим дисперсию с помощью таблицы на слайде (она есть и в вашем раздаточном материале). Заполнив первый столбец таблицы, вычислите разности значений и средней, возведите их в квадрат, заполните колонку частот, умножьте квадраты разностей на частоты. Теперь сложите полученные значения последнего столбца. Как теперь найти дисперсию? Что осталось делать?
| xi | xi-xв | (xi-xв)2 | ni | (xi-xв)2ni |
| 3 | -0,8 | 0,64 | 3 | 1,92 |
| 4 | 0,2 | 0,04 | 6 | 0,24 |
| 5 | 1,2 | 1,44 | 1 | 1,44 |
| Ʃ | 3,6 |
Итак, дисперсия равна 0,36.
Среднее квадратическое отклонение равно 0,6.
Теперь сравним результаты обучения иностранному языку в 2 подгруппах группы ЭБ-11. Во второй подгруппе и выборочная средняя, и выборочное отклонение чуть больше, чем в первой.
Как вы думаете, что означает различие в выборочных средних? Различие в средних квадратических отклонениях?
Правильно, во второй подгруппе успеваемость на 0,3 балла выше, чем в первой. При этом во второй подгруппе различия в успеваемости студентов выражены больше, чем в первой (значит, в первой подгруппе успеваемость более ровная, чем во второй).
Вывод. Таким образом, к первичным методам статистической обработки числовых данных относят: составление выборочного ряда и статистического распределения, вычисление выборочной средней, дисперсии и среднего квадратического отклонения.
Вопрос 2: Проверка гипотезы исследования методами математической статистики.
Докладчик: студент группы ЭБ-11 Ерасова Е.
С помощью вторичных методов статистической обработки экспериментальных данных можно проверять, то есть доказывать или опровергать гипотезы, связанные с экспериментом. Эти методы являются более трудными, и требуют от исследователя хорошей математической подготовки. Основными являются такие методы, как:
1) Методы сравнения элементарных статистик (выборочных средних, дисперсий и др.), характеризующих разные выборки;
2) Регрессионное исчисление;
3) Корреляционный и факторный анализ.
Мы подробно остановимся только на первой группе методов.
Перед вами на слайде 2 выборки. Допустим, начальная выборка 4, 2, 5, 3, 7, 4, 3, 1, 5, 6 представляет собой процентные значения безработных среди трудоспособного населения в разных регионах некоторой страны, и эти значения довольно велики. В результате социальной политики государства, направленной на принятие комплекса мер по борьбе с безработицей процент безработных людей в регионах немного уменьшился, что отражает конечная выборка: 0, 2, 3, 3, 5, 4, 1, 1, 3, 8. Вам заметно, что во второй выборке средняя величина безработицы меньше, чем в первой?
Выборочные средние значения соответственно равны 4 и 3, что отражено на слайде. Вопрос в том, насколько статистически достоверны эти различия? Наши вычисления показывают, что средняя величина безработицы в регионах в результате принятия мер уменьшилась на 1%. Достаточное ли это уменьшение для того, чтобы сделать вывод об успешности социальной политики? Ответ на этот вопрос зависит не только от средних величин, но и от дисперсий. Значения дисперсий также показаны на слайде. Для решения данной задачи обратимся к статистическому t-критерию Стъюдента, основанному на формуле, которую вы видите на доске:
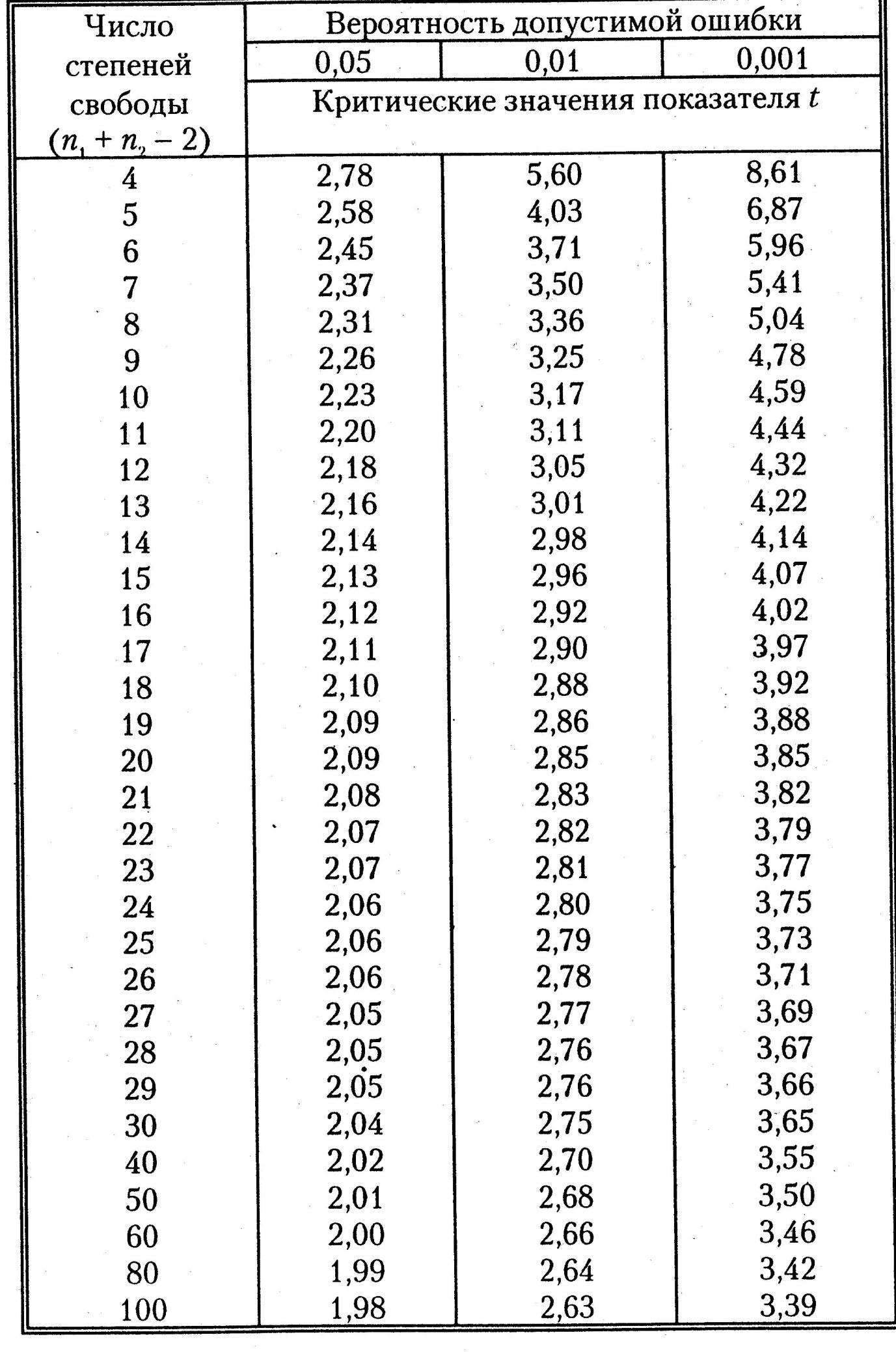
В нем x1 и x2 – выборочные средние; D1 и D2 – выборочные дисперсии; n1 и n2 – объемы двух данных выборок. Вычисляя, получаем приближенное значение 1,13, что меньше табличного критического значения 2,10 для данного объема выборки. То, что наш показатель оказался меньше критического значения в таблице, означает, что гипотеза о том, что выборочные средние показатели безработицы статистически достоверно отличаются друг от друга, не подтвердилась, то есть социальная политика, направленная на уменьшение безработицы, в этом случае является неэффективной.
Если в ходе исследования возникает необходимость сравнить дисперсии двух выборок, для этого применяется критерий Фишера, основанный на простом отношении дисперсий:
где D1 и D2 – дисперсии первой и второй выборки соответственно.
Иногда в процессе проведения эксперимента возникает задача сравнения не абсолютных средних значений, а процентных распределений данных. В этом случае ответ на вопрос об эффективности эксперимента дает χ² - критерий, основанный на формуле, которую вы видите на слайде:
В этой формуле Pi – процент значений до эксперимента; Vi – процент значений после эксперимента.
Предлагаем вам решить задачу, чтобы научиться оценивать эффективность формирующего эксперимента. Для этого возьмите каждый раздаточный материал с задачей № 2.
Задача 2. Проведите сравнительный анализ результатов среза школьных знаний по математике в группе ЭБ-11 и экзамена по математике в первом семестре по данным таблицы (см. слайд):
a) Сравните выборочные средние x1 и x2, сделайте вывод о положительной или отрицательной динамике результатов;
b) С помощью χ² - критерия и таблицы его критических значений определите, различаются ли статистически достоверно успеваемость группы по математике в начале и в конце семестра?
Вычислите среднюю оценку группы по математике в сентябре, а также среднюю в декабре по итогам экзамена. Назовите свои результаты (один учащийся называет результат, остальные голосуют сигнальными карточками).
Средний балл в сентябре составлял 3,44, тогда как в декабре 4,0. Итак, экзамен в декабре показал лучший результат, чем срез знаний в сентябре. Теперь вычислим коэффициент χ², чтобы узнать, отличаются ли результаты в сентябре и декабре статистически достоверно. Для этого вам в помощь следующая таблица, данная в раздаточном материале № 2. Заполните столбец Pi – процентное значение оценки каждого вида в сентябре, учитывая, что общее число оценок, как студентов группы – 25. Теперь заполните столбец Vi - процентное значение оценки каждого вида в декабре. Теперь подсчитайте значения последнего столбца.
Проверим полученные значения (работа с сигнальными карточками).
Теперь, сложив полученные значения последнего столбца, получим значения коэффициента χ². Что у вас получилось?
Итак, полученное значение χ² = 58,1 превышает критическое значение 16,27. Это означает, что успеваемость по математике значительно улучшилась, так как результаты отличаются статистически достоверно, при этом ошибка нашего вывода не превышает 0,001, то есть ничтожно мала.
Итог семинара. Преподаватель благодарит выступающих за проделанную интеллектуальную и организационную работу, отмечает наиболее активных участников семинара, раздает призы. В заключение преподаватель желает успеха всем, кто ведет исследовательскую работу по той или иной дисциплине, отмечая, что научно-исследовательская, в частности, проектная деятельность обучающихся является приоритетным направлением в современном профессиональном образовании.
Приложение 1. Таблица критических значений коэффициента Стюдента.
Приложение 2. Таблица критических значений коэффициента χ².
Приложение 3. Раздаточный материал № 1.
Задача 1. Дана выборка результатов обучения в 1 семестре иностранному языку в первой подгруппе:
3; 4; 4; 4; 4; 3; 4; 5; 4; 3.
a) составьте выборочный ряд и найдите размах выборки и медиану;
b) составьте статистическое распределение частот и по нему определите моду и вычислите выборочную среднюю, дисперсию и среднее квадратическое отклонение.
Выборочный ряд:______________________________________________________; медиана равна ____
Размах выборки: Δx=xmax-xmin=________________________________________________
Статистическое распределение:
Мода равна ____
Выборочная средняя:
____________________________________________________________
| Xi | Xi -Xв | (Xi -Xв)2 | ni | (Xi -Xв)2·ni |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Σ |
|
Выборочная дисперсия: = _______________________________________________________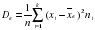
Среднее квадратическое отклонение: = __________________________________
Приложение 4. Раздаточный материал № 2.
Задача 2. Проведите сравнительный анализ результатов среза школьных знаний по математике и экзамена по математике в первом семестре по данным таблицы:
| Срез знаний (сентябрь) | Экзамен (декабрь) |
Значения 
|
|
Оценки xi |
Количество ni | Процент оценок Pi (всего – 25 оценок) |
Оценки xj |
Количество nj | Процент оценок Vi (всего – 25 оценок) |
|
| 2 | 3 |
| 2 | 1 |
|
|
| 3 | 10 |
| 3 | 4 |
|
|
| 4 | 10 |
| 4 | 14 |
|
|
| 5 | 2 |
| 5 | 6 |
|
|
a) Сравните выборочные средние x1 и x2, сделайте вывод о положительной или отрицательной динамике результатов;
b) С помощью χ² - критерия и таблицы его критических значений определите, различаются ли статистически достоверно успеваемость группы по математике в начале и в конце семестра?
Средняя оценка в сентябре: 
_______________________________________________
Средняя оценка в декабре: 
________________________________________________
__________________________________________________
8
Получите свидетельство
Вход
Сценарий семинара по математике "Математические методы в исследовательской работе" (1.37 MB)
0
899
21
Нравится
0
