"Степенные функции"

Занимательная математика

Алгебра

9 класс.

Урок на тему:

Степенные функции.

Корень кубический.

Степенные функции.

Ребята, мы продолжаем изучать степенные функции. Темой сегодняшнего урока будет функция - корень кубический из х .

А что же такое корень кубический?

Число y называется корнем кубическим из x (корнем третьей степени) если выполняется равенство

Обозначают: , где х - подкоренное число, 3- показатель степени.

Степенные функции.

Как мы видим, корень кубический можно извлекать и из отрицательных чисел . Получается, что наш корень существует для всех чисел.

Корень третьей степени из отрицательного числа равен отрицательному числу. При возведении в нечетную степень знак сохраняется, третья степень является нечетной.

Проверим равенство:

Пусть . Возведем оба выражения в третью степень

Тогда или

В обозначениях корней получаем искомое тождество.

Степенные функции.

Свойства корней кубических:

а)

б)

Давайте докажем второе свойство.

Получили что число в кубе равно

и тогда равно

что и требовалось доказать.

Степенные функции.

Ребята, давайте теперь построим график нашей функции .

1) Область определения множество действительных чисел .

2) Функция нечетная , так как Далее рассмотрим нашу функцию при х≥0 , после отразим график относительно начала координат.

3 ) Функция возрастает при х≥0 . Для нашей функции, большему значению аргумента соответствует большее значение функции, что и значит возрастание.

4) Функция не ограничена сверху . На самом деле из сколь угодно большого числа можно вычислить корень третьей степени, и мы можем двигаться до бесконечности вверх, находя все большие значения аргумента.

5) При х≥0 наименьшее значение равно 0 . Это свойство очевидно.

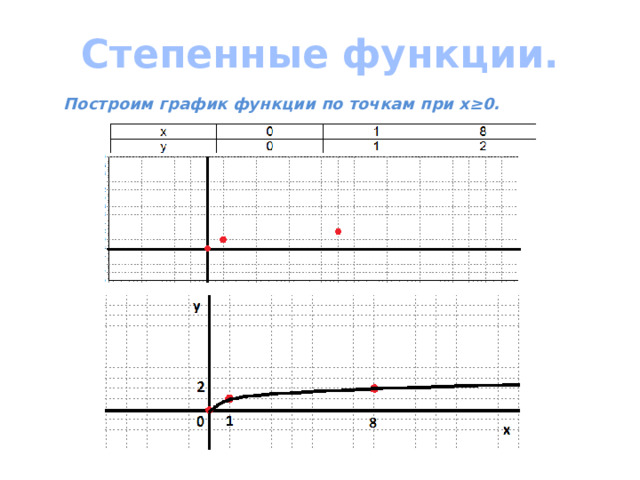
Степенные функции.

Построим график функции по точкам при х≥0.

Степенные функции.

Построим наш график функции на всей области определения. Помним, что наша функция нечетная.

Свойства функции:

1 ) D(y)=(-∞;+∞)

2) Нечетная функция.

3 ) Возрастает на (-∞;+∞)

4) Неограниченна.

5) Наименьшего и наибольшего значения нет.

6) Функция непрерывна на всей числовой прямой.

7) Е(у)= (-∞;+∞).

8) Выпукла вниз на (-∞;0], выпукла вверх на [0;+∞).

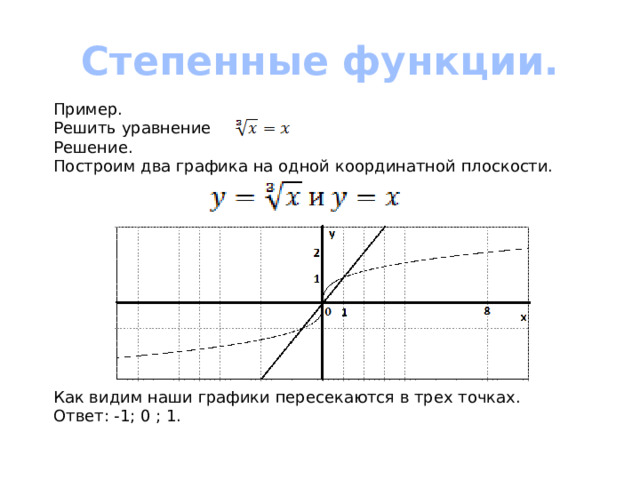
Степенные функции.

Пример.

Решить уравнение

Решение.

Построим два графика на одной координатной плоскости.

Как видим наши графики пересекаются в трех точках.

Ответ: -1; 0 ; 1.

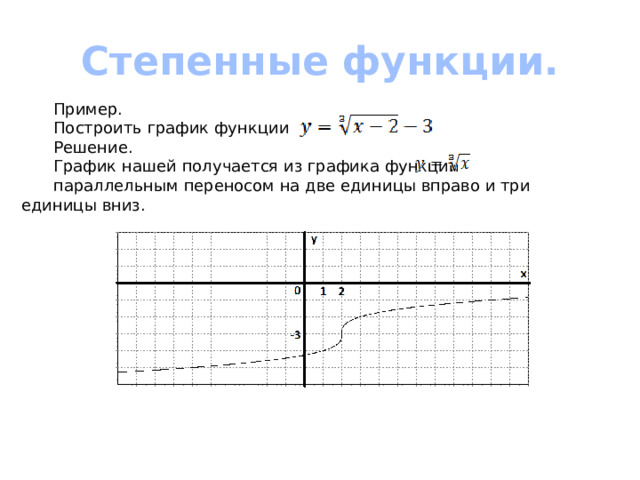
Степенные функции.

Пример.

Построить график функции

Решение.

График нашей получается из графика функции

параллельным переносом на две единицы вправо и три единицы вниз.

Степенные функции.

Пример.

Построить график функции и прочитать его.

Решение.

Построим два графика функций на одной координатной плоскости с учетом наших условий. При х≥-1 строим график корня кубического, при х≤-1 график линейной функции.

1) D(y)=(-∞;+∞)

2) Функция не является ни четной, ни нечетной.

3) Убывает на (-∞;-1], возрастает на [-1;+∞)

4) Неограниченна сверху, ограничена снизу.

5) Наибольшего значения нет. Наименьшее значение равно минус один.

6) Функция непрерывна на всей числовой прямой.

7) Е(у)= [-1;+∞)

Степенные функции.

.

Задачи для самостоятельного решения.

Решить уравнение

Построить графики функций:

а)

б)