Справочные материалы по теме «Решение уравнений»
Решение линейных уравнений и уравнений, приводимых к ним
Определение. Уравнение вида 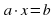 , (1)
, (1)
где 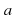 и
и 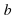 - действительные числа или выражения, зависящие от параметров, а
- действительные числа или выражения, зависящие от параметров, а 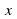 - неизвестное, называется линейным уравнением.
- неизвестное, называется линейным уравнением.
Определение. Значение переменной, которое обращают уравнение в верное равенство, называется корнем уравнения.
Определение. Решить уравнение – значит найти все его корни или доказать, что корней нет.
Определение. Два уравнения называются равносильными, если множества решений этих уравнений совпадают.
Определение. Решить уравнение, содержащее параметры, - значит указать, при каких значениях параметра существуют значения 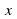 , удовлетворяющие данному уравнению.
, удовлетворяющие данному уравнению.
Уравнение (1) либо имеет единственный корень, либо имеет корнями все действительные числа, либо не имеет корней, то есть при решении линейных уравнений следует рассмотреть три случая:
Если 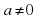 , то
, то 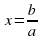 ;
;
Если 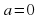 и
и 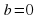 , то
, то 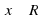 ;
;
Если 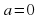 и
и 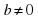 , то
, то 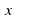 .
.
Решение квадратных уравнений и уравнений, приводимых к ним
Определение. Уравнение вида 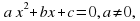 (1)
(1)
где 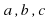 - некоторые действительные числа или выражения, зависящие от параметров, называется квадратным.
- некоторые действительные числа или выражения, зависящие от параметров, называется квадратным.
Левая его часть является квадратным трехчленом, то есть многочленом второй степени. Корни квадратного уравнения (1) находят по формуле
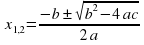 (2)
(2)
Выражение 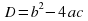 называется дискриминантом квадратного уравнения (1).
называется дискриминантом квадратного уравнения (1).
Если 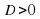 , то уравнение имеет два различных действительных корня;
, то уравнение имеет два различных действительных корня;
если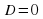 , то уравнение имеет два совпадающих действительных корня;
, то уравнение имеет два совпадающих действительных корня;
если 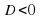 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.
То есть в зависимости от значения дискриминанта

 возможны 3 различные ситуации:
возможны 3 различные ситуации:
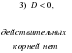
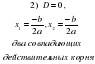
В случае, когда второй коэффициент квадратного уравнения четен, то есть  , корни удобно находить по формуле
, корни удобно находить по формуле
. (3)
Неполные квадратные уравнения, то есть такие, в которых  , удобно решать методом разложения на множители левой части уравнения.
, удобно решать методом разложения на множители левой части уравнения.
Если  - корни квадратного уравнения (1), то
- корни квадратного уравнения (1), то
 ,
,  . (4)
. (4)
Формулы (4) называются формулами Виета.
Верно и обратное утверждение: если  удовлетворяют равенствам (4), то эти числа являются корнями квадратного уравнения (4).
удовлетворяют равенствам (4), то эти числа являются корнями квадратного уравнения (4).
Для приведенного квадратного уравнения  (5)
(5)
формулы Виета приобретают вид
 ,
,  (6)
(6)
В случае, когда  , квадратный трехчлен можно разложить на множители: если
, квадратный трехчлен можно разложить на множители: если 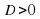 , то
, то
если 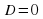 , то
, то  .
.
Определение. Квадратичной функцией называется функция вида  , где
, где 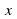 – независимая переменная,
– независимая переменная,  некоторые действительные числа, причем
некоторые действительные числа, причем 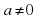 .
.
Графиком квадратичной функции является парабола.
Ее ветви направлены верх при  , и вниз при
, и вниз при  . Абсциссу вершины параболы можно найти по формуле
. Абсциссу вершины параболы можно найти по формуле  . Ординату вершины можно найти, подставив это значение в формулу.
. Ординату вершины можно найти, подставив это значение в формулу.
Свойства квадратного трехчлена:
если коэффициент при старшей степени квадратного трехчлена меньше нуля, то ветви параболы направлены вниз;
если квадратный трехчлен не имеет действительных корней, то парабола не пересекает и не касается оси абсцисс;
если график функции  находится выше оси абсцисс, то
находится выше оси абсцисс, то  , а
, а  .
.
Решение иррациональных уравнений
Определение. Иррациональными называют уравнения, в которых неизвестное содержится под знаком корня или под знаком операции возведения в дробную степень. Напомним основные свойства данных уравнений.
Все корни четной степени, входящие в уравнение, являются арифметическими, то есть подкоренное выражение определено только для неотрицательных значений, и сам корень принимает только неотрицательные значения.
Все корни нечетной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и, в зависимости от знака подкоренного выражения, могут принимать как неотрицательные значения, так и отрицательные значения.
Уравнение  равносильно системе
равносильно системе
Основными методами решения иррациональных уравнений являются:
возведение обеих частей уравнения в одну и ту же степень;
замена неизвестного;
домножение обеих частей уравненя на одну и ту же функцию;
применение свойств функций, входящих в уравнение, и использование их графиков.
Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например, возведение обеих частей уравнения в четную степень, приводят к уравнению-следствию. Это уравнение, наряду с корнями исходного уравнения, может содержать и другие корни исходного уравнения, может содержать и другие корни, которые называются постронними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние
корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Часто возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается ОДЗ уравнения и требование неотрицательности обеих частей уравнения, возводимых в четную степень. Напомним также, что возведение обеих частей уравнения в нечетную степень приводит к равносильному уравнению.
Решение уравнений, содержащих знак абсолютной величины
Определение. Модулем (абсолютной величиной) действительного числа 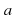 называется само это число, если
называется само это число, если  , и противоположное число
, и противоположное число  , если
, если  .
.
Обозначается  .
.
Значит,
Основной метод решения уравнений, содержащих знак модуля, состоит в следующем: область допустимых значений уравнения разбивается на множества, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак. На каждом таком множестве уравнение записывается без знака модуля и затем решается на этом множестве. Множество решений исходного уравнения составляется из решений, найденных на всех частях ОДЗ (область допустимых значений). Однако в некоторых случаях такой метод решения, основанный на определении абсолютной величины, вызывает определенные затруднения в реализации, при этом уравнение может допускать несколько иной способ решения.
Перечислим некоторые частные случаи уравнений, содержащих знак модуля.


При  уравнение решений не имеет; при
уравнение решений не имеет; при 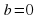 уравнение равносильно уравнению
уравнение равносильно уравнению  ; при
; при  уравнение равносильно совокупности уравнений
уравнение равносильно совокупности уравнений

, где  - некоторые функции.
- некоторые функции.
При решении уравнений указанного вида применяется метод интервалов:
определяются критические точки, то есть точки, в которых хотя бы одна из функций  меняет свой знак;
меняет свой знак;
найденные критические точки разбивают ОДЗ уравнения на промежутки, на каждом из которых все функции  сохраняют знак;
сохраняют знак;
исходное уравнение решается на каждом промежутке, при этом модули опускаются с учетом знака функций на рассматриваемом промежутке;
объединяются решения, найденные на всех частях ОДЗ.
, где  - некоторые функции.
- некоторые функции.
Метод интервалов решения уравнения указанного вида состоит в следующем:
определяются точки, в которых функция  меняет знак;
меняет знак;
Определяются точки, в которых функции  и
и  меняют знак;
меняют знак;
найденными точками ОДЗ уравнения разбиваются на промежутки;
исходное уравнение решается на каждом промежутке, при этом сначала раскрывается внутренний модуль, а затем внешний;
объединяются решения, найденные на всех частях ОДЗ.
Уравнения, решение которых основано на свойствах абсолютной величины.
Приведем без доказательства свойства абсолютной величины, которые используются при решении некоторых уравнений:





 .
.

 .
.
Решение рациональных уравнений
Определение. Дробно-рациональной функцией называется отношение многочленов, то есть  . Рациональным называется уравнение, в котором присутствуют только дробно-рациональные функции. Стандартный вид рационального уравнения – это
. Рациональным называется уравнение, в котором присутствуют только дробно-рациональные функции. Стандартный вид рационального уравнения – это
(1)
где  и
и  - многочлены
- многочлены  .
.
Уравнение (1) равносильно системе
(2)
то есть решение уравнения (1) сводится к нахождению корней уравнения  , удовлетворяющих условию
, удовлетворяющих условию  .
.
Основными методами решения рациональных уравнений являются:
приведение всех дробей к одинаковому основанию, а затем к стандартному виду (1);
метод введения новых неизвестных. Этот метод является распространенным способом решения уравнений любых видов и типов, в том числе и рациональных уравнений. В результате введения новых переменных исходное уравнение сводиться к системе уравнений (системе уравнений и неравенств) более простого вида;
метод выделения полного квадрата;
метод, основанный на применении производной пропорции. Если дана пропорция , то при любых  и любых
и любых  таких, что справедливо равенство
таких, что справедливо равенство
называется производной пропорцией.
В частности, из пропорции  можно получить следующие производные пропорции:
можно получить следующие производные пропорции:



Указанное свойство пропорции можно иногда применять при решении иррациональных уравнений. Однако следует иметь в виду, что соответствующие преобразования уравнения могут приводить как к потере корней (нули знаменателя производной пропорции), так и к появлению посторонних корней (нули знаменателя исходной пропорции).


 Получите свидетельство
Получите свидетельство Вход
Вход



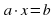 , (1)
, (1) 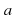 и
и 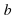 - действительные числа или выражения, зависящие от параметров, а
- действительные числа или выражения, зависящие от параметров, а 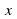 - неизвестное, называется линейным уравнением.
- неизвестное, называется линейным уравнением.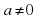 , то
, то 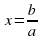 ;
;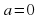 и
и 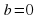 , то
, то 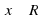 ;
;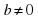 , то
, то 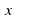 .
.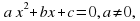 (1)
(1)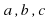 - некоторые действительные числа или выражения, зависящие от параметров, называется квадратным.
- некоторые действительные числа или выражения, зависящие от параметров, называется квадратным. 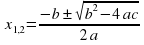 (2)
(2)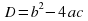 называется дискриминантом квадратного уравнения (1).
называется дискриминантом квадратного уравнения (1).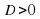 , то уравнение имеет два различных действительных корня;
, то уравнение имеет два различных действительных корня; 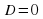 , то уравнение имеет два совпадающих действительных корня;
, то уравнение имеет два совпадающих действительных корня;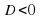 , то уравнение не имеет действительных корней.
, то уравнение не имеет действительных корней.

 возможны 3 различные ситуации:
возможны 3 различные ситуации: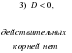
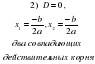









 Справочные материалы по математике по теме "Решение уравнений" (38 КB)
Справочные материалы по математике по теме "Решение уравнений" (38 КB)
 0
0 1073
1073 148
148 Нравится
0
Нравится
0


