МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
АКАДЕМИЯ СОЦИАЛЬНОГО УПРАВЛЕНИЯ
Кафедра математических дисциплин
ПРОЕКТ
Реализация требований ФГОС ООО при обучении учащихся 5 класса
теме: “Обыкновенные дроби”.
Учебник: Зубарева И. И., Мордкович А.Г. «Математика, 5 класс».
Выполнил: Группа 9,
Латышева Наталья Алексеевна,
слушатель учебного курса
«Актуальные проблемы развития
профессиональной компетентности
учителя математики
(в условиях ФГОС)»,
учитель математики
Муниципального общеобразовательного
учреждения « Лицей № 1»,
г. Подольск
Московской области
Руководитель учебного курса
Кашицына Юлия Николаевна
кандидат педагогических наук,
доцент кафедры математических
дисциплин
Москва 2013
Содержание
Введение………………………………………………………………..3
ГЛАВА 1. Теоретические основы обучения теме «Обыкновенные дроби».
§1. Требования ФГОС ООО к школьному курсу математики …………..…4
§ 2. Логико-математический анализ содержания темы……………………...7
§ 3. Виды УУД при обучении математике…………………………………...14
ГЛАВА 2. Методические рекомендации обучения теме
§ 4. Карта изучения темы и её использование……………………………….14
4.1. Диагностируемые цели обучения теме…………………………….14
4.2. Логическая структура и содержание темы………………………...16
4.3. Средства обучения теме (в том числе ИТ) ………………………….21
§ 5. Учебный план темы…………………………………………………….…23
§ 6. Примеры реализации целей обучения теме……………………………..29
ЗАКЛЮЧЕНИЕ……………………………………………………………...…38
Список литературы………………………………………………………….....39
Приложение…………………………………………………………………........41
ВВЕДЕНИЕ
Актуальность
Цель проекта: Реализация требований ФГОС ООО при изучении темы:
Для достижения поставленной цели необходимо решение следующих задач.
Задачи исследования.
1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.
2. Выполнить отбор средств обучения теме, в том числе средства ИКТ.
3. Разработать таблицу целей и карту обучения теме.
4. Составить учебную рабочую программу «Тематическое и почасовое планирование образовательных результатов освоения математики (в соответствии с темой).
5. Разработать методические рекомендации обучения теме и применить их в учебном процессе (урок , иллюстрирующий развитие и формирование УУД при обучении данной теме школьного курса математики).
Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.
ГЛАВА 1. Теоретические основы обучения теме «Обыкновенные дроби».
§1. Требования ФГОС ООО к школьному курсу математики.
Следствием внешних и внутренних тенденций в развитии общества и образования явилась разработка стандартов второго поколения. Федеральный государственный образовательный стандарт основного общего образования (далее – Стандарт) представляет собой совокупность требований, обязательных при реализации основной образовательной программы основного общего образования образовательными учреждениями, имеющими государственную аккредитацию.
Методологической основой разработки и реализации Стандарта является Концепция духовно-нравственного развития и воспитания личности гражданина России.
Стандарт устанавливает требования к результатам освоения обучающимися основной образовательной программы основного общего образования: личностным, метапредметным, предметным.
Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:
- в личностном направлении:
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
в метапредметном направлении:
1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов; 2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; 3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации; 4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации; 5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; 6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач; 7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; 8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; 9) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
в предметном направлении:
1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления; 2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений; 3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса; 5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей; 6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях; 7) овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений; 8) усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач; 9) умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур; 10) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
§2. Логико-математический анализ темы «Обыкновенные дроби».
По программе на изучение темы «Обыкновенные дроби» в 5 классе по учебнику Зубарева И. И. Математика. 5 кл.: Учеб. для общеобразоват. учреждений./ И. И. Зубарева, А. Г. Мордкович. – 14-е изд., испр. и дополн. – М.: Мнемозина, 2013. – 270с.: ил. отводится 44 часа ( при 6 часах в неделю). Это вторая глава в курсе математики 5 класса. При изучении данной темы вводятся следующие понятия :
- Основное свойство дроби.
- Правила сравнения дробей.
- Арифметические действия с обыкновенными дробями: сложение и вычитание дробей с одинаковыми и с разными знаменателями (простейшие случаи), умножение и деление обыкновенной дроби на натуральное число.
- Нахождение части от целого и целого по его части в два приема.
Ведущий способ логической организации учебного материала – индуктивный, однако на некоторых темах можно увидеть дедуктивный и комбинированные способы. На уроках используются объяснительно-иллюстративные (рассказ, лекция, беседа, демонстрация слайдов), репродуктивные (решение задач и примеров), проблемные (проблемные задачи, познавательные задачи), частично- поисковые методы обучения.
На протяжении всего курса изучения математики, алгебры, геометрии и математического анализа обучающиеся будут работать с дробями (обыкновенными, алгебраическими, десятичными). Все правила, свойства, алгоритмы, изученные в этой теме будут использоваться на протяжении всего обучения в школе, причем не только на математических дисциплинах. Без дробей и действий с ними не обойдется физика, химия, экономика, информатика, география, биология и другие предметы естественно-научного цикла.
Логико-математический анализ темы «Обыкновенные дроби» представлен в таблице 1.
Таблица 1.
| Логико-математический анализ содержания темы «Обыкновенные дроби». |
| Формулировка определения | Логический анализ | Подведение под понятие | Следствие из определения | Возможные ошибки |
| Термин | Род | Видовые отличия | Логические связи | Вид определения | Опорные знания |
|
|
|
| 1.Мама купила арбуз и разделила его на 6 равных частей. Эти равные части называют долями
| доля
| дробь
| запись
| конъюнктивная
| через род и видовые отличия
| деление
| деление целого на части
| 
| Куда записывать делимое и делитель
|
|
2. Запись вида  называют обыкновенными дробями называют обыкновенными дробями |
Обыкно-венная дробь
|
части
|
запись
|
конъюнктивная
|
через род и видовые отличия
|
доля
|
деление целого на части
|
Изображение дробей на координатной прямой
|
Что показывает знаменатель и что показывает числитель |
|
3. Дробь, в которой числитель меньше знаменателя, называют правильной дробью. Дробь, в ко-торой чис-литель боль-ше знаме-нателя или равен ему называют неправильной дробью. |
Правиль-на и неправильная дробь
|
дробь
|
дробь определяется данным знаменателем по отношению к числителю
|
конъюнктивная
|
через род и видовые отличия
|
понятие числителя и знаменателя
|   - числитель - числитель  -знаменатель -знаменатель  ,то ,то - дробь правильная - дробь правильная    ,то ,то - дробь неправиль-ная. - дробь неправиль-ная.
|
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице
|
Путают числитель и знаменатель
|
|
4.Запись числа, содержащих целую и дробную части, называют смешанной (смешанное число) |
смешанное число |
дробь |
Есть целая часть и дробная часть |
конъюнктивная
|
через род и видовые отличия |
обыкновенная дробь, натуральное число |
Сложения целой части и дробной части |
Перевод из смешанной дроби в неправиль-ную. Перевод из неправильной в смешанную дробь |
При переводе из непра-вильной дро-би путают куда писать неполное частное, ос-таток,дели-тель.При пе-реводе в смешанную дробь, что писать в знаменатель. |
Логико-математический анализ задач по теме «Обыкновенные дроби» учебника «Математика, 5 класс», И.И. Зубаревой, А.Г. Мордковича.
Теоретический материал в учебнике изложен таким образом, чтобы преподаватель смог применять проблемный подход в обучении ( учебные задания) . С помощью системы обозначений выделяются упражнения четырех уровней сложности. В каждом параграфе сформулированы контрольные задания, исходя из того, что должны знать и уметь учащиеся для достижения ими уровня стандарта математического образования. В конце учебника даны домашние контрольные работы и ответы. Цветные иллюстрации (рисунки и схемы) обеспечивают высокий уровень наглядности учебного материала.
В результате выполнения логико-математического анализа задач была проведена их классификация по уровню сложности и виду, на основании которой составлена таблица 3.
Таблица 2.
Классификация задач по теме «Обыкновенные дроби»
| Номер пар-фа | Учебные задания | I уровень сложности | II уровень сложности | III уровень сложности | IV уровень сложности
|
| § 18. | № № 279, 280, 281,283,284, 292, 293 | № 282,285, 286 | № 287- 291, 294, 297- 299. | № 295, 296. |
|
| § 19. | №№ 300- 302, 308, 309- 310 | № 303- 307, 311- 315 | № 316- 318 |
| № 319. |
| § 20. | №№ 320, 324. | №№ 321, 322, 325, 326. | №№ 323, 327- 340. |
|
|
| § 21. | №№ 341- 346, 355 | №№ 347- 354, 356, 357, 365, 366, 367, 370, 371, 375,374. | №№ 358- 364, 372, 373. | № 369. |
|
| § 22. | №№ 376, 382, 383, 390- 392 | №№ 377, 384- 389, 393, 394, 396- 403. | №№ 378- 381, 395, 404 |
|
|
| § 23. | №405 | №№ 406, 407, 409, 410, 413, 414 | №№ 408, 415, 416, 418, 419 | №№ 411, 412, 417. |
|
| § 24. | №№ 420, 421, 435, 436, 437.;38, 439, 448 | №№ 422-426, 428, 429, 433, 461, 462 | №№ 427, 430,434, 440, 441- 447, 449- 459 | №№ 431, 432,460, 463. |
|
| § 25. | №№ 464, 465 | №№ 466- 470, 477, 478 | №№ 471, 472 | №№ 473, 474, 475, 476 |
|
| § 26. | №№ 479, 480, 490, 491, 492 | №№ 482- 484, 493- 496, 501, 502 | №№ 485, 486, 497- 500 | №№ 488, 489, 503, 504. |
|
§ 3. Виды УУД при обучении математике.
Таблица 3
Список универсальных учебных действий (УУД)
| Название УУД | Условное сокращение |
Познавательные УУД | ПОД 1 |
Познавательные общеучебные действия | 1.1 – 1.3 |
| 1.1.0 принятие и сохранение познавательной цели (учебной задачи); 1.1.1.самостоятельное выделение и формулирование познавательной цели (учебной задачи); 1.1.2.поиск необходимой информации и её понимание (смысловое чтение, определение основной и второстепенной информации); 1.1.3 структурирование информации и знаний (в т.ч. составление текстов) и её понимание; 1.1.4 выполнение знаково-символических действий (в т.ч. моделирования); 1.1.5 выбор эффективных способов решения задач в зависимости от конкретных условий; 1.1.6 построение речевых высказываний в устной и письменной формах (подробный и сжатый пересказ текста); 1.1.7 рефлексия способов и условий действия; 1.1.8 самоконтроль и самооценка процесса и результатов деятельности; | 1.1.0 1.1.1 1.1.2 1.1.3 1.1.4 1.1.5 1.1.6 1.1.7 1.1.8 |
Познавательные логические учебные действия | 1.2 |
| 1.2.1 сравнение; 1.2.2 подведение под понятие; 1.2.3 анализ объектов для выделения свойств и признаков объектов; 1.2.4 синтез (в т.ч. самостоятельное достраивание, восполнение недостающих компонентов); 1.2.5 выведение следствий; 1.2.6 сериация и классификация; 1.2.7 установление причинно - следственных связей; 1.2.8 построение логической цепи рассуждения; 1.2.9 доказательство | 1.2.1.- 1.2.9 |
Познавательное действие «Постановка и решение проблем» | 1.3 |
| 1.3.1 формулирование проблемы; 1.3.2. выдвижение гипотез и их обоснование; 1.3.3 самостоятельное создание способов решения проблем творческого и поискового характера | 1.3.1 – 1.3.3. |
| Коммуникативные УУД | 2 |
| 2.1. Действия для осуществления совместной деятельности (в т.ч. работа в группе) | 2.1. |
| 2.1.1 планирование учебного сотрудничества с учителем и сверстниками; 2.1.2 инициативное сотрудничество в поиске и сборе информации; 2.1.3 разрешение конфликтов – выявление проблемы конфликта, поиск способов устранения, принятие решения и его реализация; 2.1.4 управление поведением партнёра – контроль, коррекция, оценка действий партнёра; | 2.1.1 2.1.2 2.1.3 2.1.4 |
| 2.2. Действия для осуществления общения и взаимодействия | 2.2 |
| 2.2.1. строить монологические высказывания в устной форме (достаточно полно и точно выражать свои мысли в соответствии с задачами и условиями коммуникации); 2.2.2 слушать и понимать сообщать мнения и взгляды других (высказанные в устной и письменной формах); 2.2.3 сообщать в устной и письменной формах мнения и взгляды других; 2.2.4 использовать речевые средства для дискуссии и аргументации своей позиции; 2.2.5 владеть монологической и диалогической формами речи в соответствии с нормами родного языка 2.2.6 взаимоконтроль, взаимооценка УПД | 2.2.1
2.2.2 2.2.3 2.2.4 2.2.5 2.2.6 |
| 3. Регулятивные УУД | 3 |
Постановка учебной цели в процессе освоения учебной информации; 2) выявление объективной учебной информации, необходимой для освоения; 3) соотнесение выявленной учебной информации с собственными знаниями и умениями; принятие решения об использовании помощи; 4) составление и реализация плана деятельности при освоении учебной информации; 5) контроль усвоения учебной информации; 6) оценивание результатов выполненной деятельности; 7) самодиагностика и коррекция собственных учебных действий |
|
Таблица 4
Взаимосвязь целей и УУД
| Обозначение цели | Цели обучения математике на уровне учебной темы | УУД |
| Ц 1 | приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) свойств, теорем; в) типов задач | используются и формируются познавательные логические УУД – ПЛ и действия постановки и решения проблем - ПРП |
| Ц 2 (и Ц 4, Ц 5) | контроль усвоения теоретических знаний: а) геометрических понятий; б) свойств, теорем; в) типов и классов задач | используются и формируются познавательные общеучебные и регулятивные УУД |
| Ц 3 (и Ц 4, Ц 5) | применение знаний и интеллектуальных умений при решении математических и учебных задач | используются и формируются познавательные, коммуникативные, регулятивные УУД |
| Ц 4 | применение знаний и интеллектуальных умений при решении математических и учебных задач | используются и формируются познавательные, коммуникативные, регулятивные УУД |
| Ц 5 | развитие организационных умений | формируются и используются регулятивные и познавательные общеучебные УУД |
ГЛАВА 2. Методические рекомендации обучения теме.
§ 4. Карта изучения темы и её использование.
4.1. Диагностируемые цели обучения теме.
Таблица 5
Диагностируемые цели обучения теме «Обыкновенные дроби».
| Формулировки обобщённых целей | Формулировки учебных задач, с помощью которых достигается обобщённая цель | Средства помощи |
| цель считается достигнутой, если Вы на уровнях: |
| первом | втором | третьем |
| Ц 1: приобретение УИ, формирование логических ПУД | а) анализирует текст учебника и составляет схему определения понятий; б) анализирует решение задач из учебника, обобщает их решение помощью готового предписания в) подводит решение задачи под готовое предписание. | а) строит логической цепи рассуждения; выдвижение гипотез, их обоснование на сравнение, сверяясь с учебником; б) выполняет анализ и выявляет преобразования для выделения целой части числа и представлению смешанного числа в виде неправильной дроби; в) обобщает решение задач одного типа и составляет предписание, используя карточку-информатор. | а) даёте определение всех видов обыкновенных дробей; знаково-символические действия; б) выполняете анализ и выявляете действий, нужные для сложения и вычитания смешанных дробей, в) составляете приёмы их решений с помощью указаний г) используете приобретенные знания и умения в межпредметных связях (информатика, экономика, технология); д) используете справочную литературу для получения информации по данной теме | а) карточки-информаторы; б) алгоритмы выполнения действий с обыкновенными дробями; в) алгоритмы сравнения обыкновенных дробей; г) макет: «Доли и дроби»; д) таблица окружности и круга |
|
Ц 2: кон-троль усвоения теории; формирование | знает а) определения: 1) окружности, круг, радиус, диаметр круга и окружности, полуокружность, дуга окружности; 2) что такое деление с остатком, как называются компоненты при делении с остатком; обыкновенные дроби, что показывает числитель, знаменатель, 3) правильные и неправильные дроби; 4) смешанные числа;5) дополнительный множитель; 6) деление и дроби; 7) основное свойство дроби; б) формирует законы и правила: 1) выполнения арифметических действий, 2) сравнения дробей с одинаковым знаменателем, 3) нахождение неизвестных компонентов, 4) сложения и вычитания обыкновенных дробей с одинаковыми знаменателями; 5) распознавания правильные и неправильные дроби; 6) приведения дробей к новому знаменателю, 7) приведения дробей к общему знаменателю; 8) сложение и вычитания дробей с разными знаменателями; 8) сложения и вычитания смешанных чисел; 9) умножения и деления дроби на натуральное число; 10) нахождения части от целого в) проговаривает алгоритмы: 1) сравнение дробей; 2) сложение и вычитание дробей с одинаковыми знаменателями; 3) сложения и вычитания дробей с разными знаменателями; 4) сложение и вычитание смешанных чисел; 5) выделения целой части числа и представлению смешанного числа в виде неправильной дроби;6) умножения и деления обыкновенной дроби на натуральное число; г) приводите примеры в соответствии с определениями; д) рассказывает краткие сведения из истории возникновения дробей. | знает виды обыкновенных дробей и их определения; применяет свойства сложения и вычитания; у понимает мировоззренческое значение обыкновенных дробей | 1) алгоритмы выполнения действий с обыкновенными дробями; 2) приём саморегуляции; 3) таблицы с предписаниями; 4) карточки-информаторы
|
| Ц 3: применение знаний и умений | Умеет: изображать окружность данного радиуса с помощью циркуля; распознавать точки, принадлежащие окружности (кругу) и не принадлежащие им выполнять деление с остатком читать и записывать обыкновенную дробь; находить значение дроби о числа и число по значению его дроби сравнивать дроби с одинаковыми знаменателями; распознавать правильные и неправильные дроби; складывать и вычитать дроби с одинаковыми знаменателями, смешанные числа складывать и вычитать дроби с разными знаменателями; умножать и делить дробь на натуральное число; представлять частное в виде дроби и наоборот; записывать натуральное число в виде дроби с заданным наменателем представлять смешанное число в виде суммы целой и дробной частей; в виде неправильной дроби; выделять целую часть из неправильной дроби находить часть от целого |
1) приём саморегуляции; 3) таблицы с предписаниями; 4) карточки-информаторы 5)стандарты решений обыкновенных дробей |
| б) использовать основные алгоритмы и предписания для выполнения заданий 1-ого уровня сложности; в) использовать прием саморегуляции для выполнения заданий 1-ого уровня сложности | б) использовать все основные алгоритмы и предписания для выполнения заданий 2-го уровня сложности; в) использовать прием саморегуляции для выполнения заданий 2-го уровня сложности | б) использовать все основные алгоритмы и предписания для выполнения заданий 3-го уровня сложности; в) использовать прием саморегуляции для выполнения заданий 3-го уровня сложности |
| Ц 4: формирование КУД | Ц 4: а) работаете в группе, оказываете взаимопомощь, рецензируете ответы товарищей; б) организуете взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; в) оказываете помощь, работающим на предыдущих уровнях; г) осуществляете поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия | приёмы контроля, оценки; |
| Ц 5: формирование общих ПУД и РУД | Ц 5: а) выбираете уровни достижения целей и формулируете цели своей учебной деятельности; б) выбираете задачи и решает их; в) осуществляете самопроверку с использованием образцов, приёмов; г) составляете контрольную работу для своего уровня усвоения; д) оцениваете свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делаете выводы о дальнейших действиях, планирует коррекцию учебно-познавательной деятельности | приёмы саморегуляции УПД |
4.2. Логическая структура и содержание темы.
Таблица 6
Логическая структура и содержание темы
| I. Логическая структура целей изучения темы (таблица целей) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Ц 1,5 | Ц 2-4 | Ц 1-2-4 | Ц 1,4,5 | Ц 2-4 | Ц 2 -4 | Ц 1-2-4 | Ц 1,5 | Ц 1,3-4 | Ц 2-4 | Ц 3-5 | Ц 3,5 | Ц. 1 | Ц 2-4 | Ц 1,3-4 | Ц 3-4 | Ц 3,5 | Ц 1 | Ц 2-4 | Ц. 2-4 | Ц 2-4 | Ц 1,4 | Ц 2-4 |
| П. 18 | П. 18
| П. 18 Тест
| П. 19 | П. 19 | П. 19
| П. 19 Тест | П. 20 | П. 20
| П. 20 | П. 20 | П. 20 Самост.работа | П. 21 | П. 21 | П. 21 | П. 21 | П. 21 Самост. работа | П. 22 | П. 22 | П. 22 | П. 22 Сам.работа | П.23 | П. 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
|
| Ц. 2-5 | Ц. 3, 5 | Ц. 1 | Ц. 2-4 | Ц. 2- 4 | Ц. 2, 3,5 | Ц. 2-4 | Ц.2-5 | Ц.1 | Ц.2-4 | Ц.2-4 | Ц.2-4,5 5 | Ц.2-4 | Ц3, 5 | Ц. 1 | Ц 2-4 | Ц. 2-4 | Ц. 2,5 | Ц 2-4 | Ц. 5 | Ц. 2-5 |
| Подготовка к контрольной работе. | Контрольная работа №4 | П.24 | П.24 | П.24 | П.24 Тест | П.24 | П.24 Сам.работа | П.25 | П.25 | П.25 | П.25 Тест | П.25 | П.25 Сам.работа | П. 26 | П. 26 | П. 26 | П. 26 Тест | П. 26 | Контрольная работа №5 | Урок коррекции |
| II. Блок актуализации знаний учащихся |
| Знать: (иметь) представление об окружности, обыкновенных дробях, смешанных числах что такое деление с остатком что показывает числитель и знаменатель определение правильной и неправильной дробей правила сложения и вычитания дробей с одинаковыми знаменателями правило приведения дробей к новому знаменателю правило сложения и вычитания дробей с разными знаменателями правила сложения и вычитания смешанных чисел правило умножения и деления дроби на натуральное число Уметь: изображать окружность данного радиуса с помощью циркуля, обозначать и называть их элементы, распознавать точки, принадлежащие окружности (кругу) и не принадлежащие им читать и записывать обыкновенную дробь; называть числитель и знаменатель дроби и объяснять, что ни показывают. находить значение дроби от числа и число по значению его дроби сравнивать дроби с одинаковыми знаменателями; изображать их на числовом луче распознавать правильные и неправильные дроби; отмечать их на координатном луче записывать результат деления двух любых натуральных чисел с помощью обыкновенных дробей. записывать любое натуральное число в виде обыкновенной дроби. сравнивать правильные и неправильные дроби с единицей и друг с другом. приводить дробь к новому знаменателю складывать и вычитать дроби с одинаковыми знаменателями, с разными знаменателями ,смешанные числа представлять частное в виде дроби и наоборот; записывать натуральное число в виде дроби с заданным знаменателем представлять смешанное число в виде суммы целой и дробной частей; в виде неправильной дроби; выделять целую часть из неправильной дроби находить часть от целого умножать и делить дробь на натуральное число |
|
III. Предметные результаты (Ц 2, 3 таблицы целей): уметь решать вычислительные примеры на сложение и вычитание дробей с одинаковыми и разными знаменателями, сравнивать дроби с одинаковыми и с разными знаменателями, распознавания правильные и неправильные дроби; отмечать их на координатном луче и применять полученные знания для решения текстовых задач, используя понятия: определение правильной и неправильной дроби, смешанной дроби, алгоритмы 1) сравнение дробей; 2) сложение и вычитание дробей с одинаковыми знаменателями; 3) сложение и вычитание дробей с разными знаменателями; 4) сложение и вычитание смешанных чисел; 5) выделения целой части числа и представлению смешанного числа в виде неправильной дроби; применение формул: правил сложения и вычитания с одинаковыми и разными знаменателями с помощью букв
|
| IY. Образцы заданий итоговой контрольной работы (Ц 5) |
| Контрольная работа № 4 |
| Уровневая дифференциация заложена в рейтинговой контрольной работе. Каждое задание оценивается определенным количеством баллов. Итоговая оценка за работу выставляется по следующим критериям: Вся работа – 21 балл. Отметка «5» - от 17 баллов, отметка «4» - от 12 баллов, отметка «3» - от 8 баллов. |
| Задания работы. | Баллы | Средства обучения теме |
| 1. Сократите дробь: а) 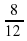 ; б) ; б)  . . 2.Сравните дроби: а)  ; б) ; б)  ; в) ; в) 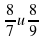 . . 3. Девочка прочитала 75 страниц, что составило  книги. Сколько страниц в книге? книги. Сколько страниц в книге? 3. Площадь тепличного хозяйства,  которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами. которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами. 4. Представьте смешанное число в виде неправильной дроби: а) 1 ; б) 23 ; б) 23 . . 5. Представьте неправильную дробь в виде смешанного числа: а)  ; б) ; б)  . . 6. Две окружности имеют общий центр. Радиус одной окружности – 4 см, а радиус второй окружности составляет 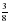 диаметра первой. Начертите эти окружности. диаметра первой. Начертите эти окружности.
7. Сколько километров пройдет катер за 5 ч, двигаясь по течению реки, если известно, что скорость течения реки 3 км/ч и это составляет  собственной скорости катера? собственной скорости катера?
| 2 3
2 2 2
2 4
4
2
3
| 1) алгоритм сокращения дроби; 2) алгоритм сравнений обыкновенных дробей; 3)алгоритм нахождения части от целого; 4) алгоритм нахождения целого по его части; 5) прием перевода смешанного числа в виде неправильной дроби;. 6) прием выделения целой части; 7) формула вычисления радиуса окружности; практический навык построения окружности с помощью циркуля; алгоритм нахождения части числа; 8) формула нахождения пути, прием нахождения скорости при движении по реке, алгоритм нахождения части от целого.
|
| Контрольная работа № 5 |
| Уровневая дифференциация заложена в рейтинговой контрольной работе. Каждое задание оценивается определенным количеством баллов. Итоговая оценка за работу выставляется по следующим критериям: Вся работа – 21 балл. Отметка «5» - от 19 баллов, отметка «4» - от 14 баллов, отметка «3» - от 8 баллов. |
| Задания работы | Баллы | Средства обучения теме |
| 1. Вычислите: а)  (1 балл); б) 3 (1 балл); б) 3 – 1 – 1 + 5 + 5 (1 балл); в) (1 балл); в)  (2 балла) (2 балла) 2. Выполните действия: а)  : 7 (1 балл); б) : 7 (1 балл); б)  3(1 балл) ; в) 3 3(1 балл) ; в) 3 (2 балла). (2 балла). 3. Найдите корень уравнения: а) 4у= (2 балла); б) х:9= (2 балла); б) х:9= (2 балла); в) (2 балла); в)  (2 балла). (2 балла). 4. За первую неделю бригада выполнила  всей работы по строительству дома, а за вторую – всей работы по строительству дома, а за вторую –  всей работы. всей работы. Какую часть работы осталось выполнить бригаде? (3 балла) 5. Один экскаватор за день работы выкапывает  часть котлована, а второй – часть котлована, а второй –  . . Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно? (4 балла) |
4
4
6
3
4 | 1) алгоритмы сложения и вычитания обыкновенных дробей, смешанных чисел; 2)алгоритмы умножения и деления обыкновенной дроби и смешанного числа на натуральное число; 3) прием саморегуляции при решении уравнений; приемы нахождения неизвестных множителя, делимого или делителя; алгоритмы умножения и деления обыкновенных дробей;. 4) применение алгоритмов сложения и вычитания обыкновенных дробей при решении текстовых задач; 5) решение задач на совместную работу, алгоритмы сложения дробей и умножения дроби на натуральное число. |
| Y. Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5) |
| 1 уровень (обязательный уровень стандарта): №№ 286,289,305(в, г), 307(в, г), 311(б), 314, 321(в, г), 322(в, г), 348, 350, 353, 357, 365, 370, 374, 387, 394, 398, 403, 406( в, г), 407(в, г), 414, 424, 426, 461(1), 462(б, в), 467, 469, 477, 484, 494, 496, 502 |
| 2 уровень: №№ 290,299, 317, 323(б), 329, 330, 333, 335, 337, 340, 359, 363, 373, 379, 381, 395(б), 404, 408(б), 418(б), , 427, 434, 441, 443, 445, 447, 450, 452, 454, 456, 459, 472, 486, 498 |
| 3 уровень: №№ 296, 369, 412, 417, 431, 463, 474, 476, 489, 504 |
| 4 уровень: №№ (со звёздочкой) №319 |
| YI. Темы индивидуальных заданий (Ц 5) |
| 1) Солнечные часы; 2) Монеты в старину на Руси; 3) Название дробей в старинных книгах; 4) История возникновения дробей, их обозначение. 5) Рассказ о числе 6) Математические факты связанные с кругом. 7) Старинные задачи на дроби |
| YII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5) |
| Познавательные УУД | Регулятивные УУД | Коммуникативные УУД | Личностные УУД |
самостоятельное выделение и формулирование учебной цели; знаково-символические действия; выбор оснований и критериев для сравнения, построение логической цепи рассуждения; выдвижение гипотез, их обоснование; обобщение, конкретизация, анализ; составление схемы определения понятия, подведение под понятие; постановка и решение проблемы при составлении задачи, осуществляют поиск и выделение необходимой информации
| Выбор и принятие целей, составление плана, самоконтроль, самооценка, соотнесение своих знаний с той учебной информацией, которую нужно усвоить; приёмы саморегуляции, оценивают достигнутый результат, самостоятельно формируют познавательную цель и строят действия в соответствии с ней.
| Взаимоконтроль, взаимопроверка, распределение обязанностей в группе, умение слушать, выступать, рецензировать, писать текст выступлений, обмениваться знаниями между членами группы для принятия эффективных совместных решений, разрешать конфликты на основе согласования позиций и учёта интересов; формулировать, аргументировать и отстаивать своё мнение; умение осознанно использовать речевые средства в соответствии с задачей коммуникации, для выражения своих чувств, мыслей и потребностей | Рефлексия собственной деятельности, самопознание и самоопределение, смыслообразование. способность ставить цели и строить жизненные планы
|
4.3. Средства обучения теме (в том числе ИТ)
Цифровые образовательные ресурсы:
http://school-collection.edu.ru/catalog/rubr/c27e8cd5-c3e0-4724-ad9d-737d78c0d95f/ (презентации ко всем урокам темы).
Разработки уроков:
1. Урок «Деление с остатком». http://www.openclass.ru/node/87134
2. Контрольные работы. http://nsportal.ru/shkola/raznoe/library/kontrolnye-raboty-5-klass-k-uchebniku-iizubareva-agmordkovich
3.Итоговый урок по теме «Обыкновенные дроби». http://school-collection.edu.ru/catalog/res/5f9d278f-c3cf-4ff5-bc79-b443bda5f644/?fullView=1
4. Презентация к уроку математики "Обыкновенные дроби"
http://www.uchportal.ru/load/25-1-0-24144
5. Урок «Сложение и вычитание обыкновенных дробей» http://nsportal.ru/shkola/algebra/library/otkrytyi-urok-slozhenie-i-vychitanie-obyknovennykh-drobei
6. Урок «Обыкновенные дроби» http://nsportal.ru/shkola/raznoe/library/konspekt-uroka-0
7. Урок по теме: «Обыкновенные дроби. Дробь, как результат деления натуральных чисел» http://metodisty.ru/m/files/view/Oreshko-droby
8.Тест по теме «Обыкновенные дроби» http://egeurok.ru/load/matematika_5_klass/testy_po_matematike_5_klass/test_po_matematike_obyknovennye_drobi/28-1-0-253
9. Урок «Правильные и неправильные дроби. Смешанные числа» http://zaz.gendocs.ru/docs/2800/index-1715135.html
10. Урок ознакомления с новыми знаниями «Обыкновенные дроби» http://textarchive.ru/c-1381815.html
11.Планирование к учебнику «Математика. 5 класс» ,Зубарева И.И., Мордкович А.Г. , раздел «Обыкновенные дроби» http://www.school-collection.edu54.ru/catalog/rubr/c27e8cd5-c3e0-4724-ad9d-737d78c0d95f/
12. Презентации к урокам темы «Обыкновенные дроби» http://www.school- http://www.school-collection.edu54.ru/catalog/rubr/c27e8cd5-c3e0-4724-ad9d-737d78c0d95f/
13. Деление с остатком. 5-й класс http://festival.1september.ru/articles/610810/
14.Доли. Обыкновенные дроби. http://festival.1september.ru/articles/616869/
15. Умножение и деление обыкновенных дробей. Нахождение дроби от числа, числа по заданной дроби http://festival.1september.ru/articles/599296/
16.Сложение дробей с разными знаменателями
http://festival.1september.ru/articles/615772/presentation/1.JPG
17. Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями http://festival.1september.ru/articles/611127/
Учебная литература:
1. И.И.Зубарева, И.П.Лепешонкова «Тетрадь для контрольных работ» , стр.46-71 ( 6 вариантов).
2. Тесты по математике. 5 класс. К учебнику Зубаревой И.И., Мордковича А.Г. - Рудницкая В.Н., стр. 37-65.
3. И.И Зубарева, М.С.Мельштейн, М.Н.Шанцева Самостоятельные работы,
5 класс, стр.41-71.
4. В.Г.Гамбарин, И.И. Зубарева Сборник задач и упражнений по математике, 5 класс, стр. 41-66.
Средства помощи при обучении теме «Обыкновенные дроби».(Приложения №№1-8)
§ 5. Учебный план темы.
Утверждаю Согласовано Рассмотрено
директор СОШ № __ зам. директора по УВР на заседании ШМО
__________ Ф.И.О. _____________ Ф.И.О. протокол № ________
от ________________
руководитель ШМО
___________ Ф.И.О.
Тематическое и почасовое планирование образовательных результатов освоения математики
на 2013/2014 учебный год (фрагмент)
Класс: 5
Учитель: Латышева Наталья Алексеевна
Количество часов: на учебный год: 210 в неделю: 6
Плановых контрольных уроков: : 10, I ч.-2, II ч.- 2, III ч.- 3, IV ч.-3.
Планирование составлено на основе источников:
1) Зубарева И.И., Мордкович А.Г. Программы. Математика 5-6 классы. Алгебра 7-9 классы. Алгебра и начала анализа 10-11 классы. М.: Мнемозина, 2011.
2) Зубарева И.И., Мордкович А.Г. Математика.5 класс. Учебник для учащихся общеобразовательных учреждений. М.: Мнемозина, 2013 г.
3) Зубарева И.И., Мордкович А.Г. Математика 5-6 классы. Методическое пособие для учителя. М.: Мнемозина, 2013 г.
4) Зубарева И.И., Лепешонкова И.П. Математика 5 класс: Тетрадь для контрольных работ ( в двух частях). М.: Мнемозина, 2012 год.
5) Зубарева И.И., Мильштейн М.С., Шанцева М.Н. Математика 5 класс. Самостоятельные работы. М.: Мнемозина, 2013 г.
Тематическое планирование составила: _Латышева Наталья Алексеевна Дата 2013 Роспись_____________
Условные обозначения: ПУУД – познавательные УУД;
ПЛ УУД - познавательные логические УУД;
ПО УУД - познавательные общеучебные УУД;
РУУД – регулятивные УУД;
КсУУД – коммуникативные УУД сотрудничество;
КрУУД – коммуникативные УУД для общения: развитие устной и письменной речи;
Ц1 – Ц 5 – цель 1 – 5; ДЗ – домашнее задание;
УПД – учебно-познавательная деятельность.
| № уро- ков | Раздел, тема урока | Форма урока; форма обучения | Предметные и метапредметные результаты Ц 1 (ПЛ УУД), Ц 2 (ПО УУД, РУУД), Ц 3 , Ц 4 (КсУУД, КРУУД), Ц 5 (ПОУУД, РУУД) |
| 1 - 23 | Название темы: «Обыкновенные дроби» Средства обучения 1) таблицы….. 2) подсказки к поиску решения задач; 3) предписания… 4) карточки с приёмами; 5) Карта темы | Уроки: семинар, практикум, лекция, др. Фронтальная, индивидуальная групповая формы обучения | Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) алгоритмов; в) типов задач Ц 2: контроль усвоения теоретических знаний: а) математических понятий; б) правил, алгоритмов; в) типов и классов задач Ц 3: применение знаний и интеллектуальных умений при решении учебных задач Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД Ц 5: развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД) |
| 1 | Деление с остатком | Урок ознакомления с новым материалом | Ц 5: Введение в тему, постановка и формулирование целей своей учебной деятельности; Ц 1: Развитие познавательных УУД : умение выделять существенную информацию из текстов разных видов.
|
| 2 | Деление с остатком | Урок формирования и применения знаний, умений и навыков. Фронтальный опрос, работа в группах, работа у доски | Ц 2: контроль усвоения изученного материала в процессе изучения нового материала Ц 3: научиться выражать делимое через неполное частное и остаток, находить остаток от деления суммы и разности двух чисел, если известны остатки данных чисел; Ц 4: формирование навыков учебного сотрудничества в ходе индивидуальной и групповой работы
|
| 3 | Деление с остатком | Комбинированный урок. Текущий тестовый контроль, работа у доски и в тетрадях. Фронтально-индивидуальная | Ц 2: тестовый контроль усвоения изученного материала Ц 3: научиться применять деление с остатком для решения задач. Ц 4: способствовать формированию научного мировоззрения |
| 4 | Обыкновенные дроби | Урок изучения нового материала | Ц 1: уметь осуществлять сравнение и классификацию по заданным критериям; научиться записывать частное в виде дроби, правильно читать и записывать обыкновенные дроби, назвать их числитель и знаменатель Ц 4:организовывать и планировать учебное сотрудничество с учителем и одноклассниками Ц5:формирование навыков аниза, индивидуального и коллективного проектирования
|
| 5 | Обыкновенные дроби | Урок закрепления знаний. Работа у доски, индивидуальная работа (карточки).
| Ц 2: использует предписания для решения типов задач своего уровня сложности; контроль усвоения изученного материала в процессе изучения нового материала Ц 3: аналогичные, обратные задачи и решает, используя помощь Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
|
| 6 | Обыкновенные дроби | Групповая работа Индивидуальная | Ц 2: контроль ( самоконтроль, взаимоконтроль) усвоения изученного материала в процессе решения задач Ц 3: аналогичные, обратные задачи и решает, используя помощь Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
|
| 7 | Обыкновенные дроби | Практикум. Текущий тестовый контроль. | Ц2: тестовый контроль усвоения изученного материала Ц3: освоить два способа получения дроби и научиться применять их при решении задач Ц4: уметь точно и грамотно выражать свои мысли |
| 8 | Отыскание части от целого и целого от его части | Урок ознакомления с новым материалом. Фронтальная работа, работа с текстом учебника. | Ц 1: Введение в тему, постановка и формулирование целей своей учебной деятельности; вывести алгоритм нахождения части от целого и научиться применять его при решении задач Ц 5: применять таблицы, схемы, модели для получения информации
|
| 9 | Отыскание части от целого и целого от его части | Урок формирования и применения знаний, умений и навыков. Фронтальный опрос, работа в парах, работа у доски и в тетрадях. | Ц1: вывести алгоритм нахождения целого по его части Ц3: научиться применять алгоритм нахождения целого по его части при решении задач Ц4: уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации |
| 10 | Отыскание части от целого и целого от его части | Урок закрепления знаний, умений и навыков. Работа у доски, самостоятельная работа. | Ц2: классифицировать задачи на части по методу решения Ц3: произвольно и осознанно владеть общим приемом решения задач, осуществлять поиск необходимой информации для выполнения учебных задач Ц4: формировать коммуникативные действия , направленные на структуирование информации по данной теме |
| 11 | Отыскание части от целого и целого от его части | Практикум. Работа в группах. | Ц3: : произвольно и осознанно владеть общим приемом решения задач, осуществлять поиск необходимой информации для выполнения учебных задач Ц4: определять цели и функции участников, способы взаимодействия Ц5: развитие организационных навыков |
| 12 | Отыскание части от целого и целого от его части | Самостоятельная работа. | Ц3, Ц5:выбирает задачи своего уровня сложности и решает из самостоятельно |
| 13 | Основное свойство дроби | Урок освоения новых знаний Работа с текстом учебника, фронтальная работа с классом. | Ц1: вывести основное свойство дроби, научиться записывать его в буквенном виде и познакомиться с его применением |
| 14 | Основное свойство дроби | Урок формирования и применения знаний, умений и навыков. Математический диктант, работа у доски. | Ц2: контроль усвоения определения основного свойства дроби Ц3: научиться применять основное свойство дроби для сокращения дробей Ц4: поддерживать инициативное сотрудничество в поиске и сборе информации |
| 15 | Основное свойство дроби | Комбинированный урок. Индивидуальная работа (карточки), работа у доски | Ц1: вывести алгоритм приведения дробей к общему знаменателю Ц3: научиться применять алгоритм приведения к общему знаменателю для сравнения дробей, решения задач Ц4: воспринимать текст с учетом поставленной задачи, находить в тексте информацию, необходимую для ее решения |
| 16 | Основное свойство дроби | Урок закрепления знаний. Работа фронтальная, индивидуальная. | Ц3: систематизировать умения и навыки учащихся по теме «Основное свойство дроби»; решать задачи своего уровня сложности Ц4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
|
| 17 | Основное свойство дроби | Самостоятельная работа. | Ц : 3, 5: выбирает задачи своего уровня сложности , решает их; |
| 18 | Правильные и не правильные дроби. Смешанные числа | Урок овладения новыми знаниями, умениями, навыками. | Ц1: научиться различать правильные и неправильные дроби, изображать правильные и неправильные дроби на координатном луче, сравнивать их с единицей |
| 19 | Правильные и не правильные дроби. Смешанные числа | Урок формирования и применения знаний, умений и навыков | Ц2: : контроль ( самоконтроль, взаимоконтроль) усвоения изученного материала в процессе решения задач Ц3: научиться выделять целую часть из неправильной дроби, записывать смешанное число в виде неправильной дроби Ц4: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы |
| 20 | Правильные и не правильные дроби. Смешанные числа | Урок – практикум. Индивидуальная и групповая работа | Ц2: : контроль ( самоконтроль, взаимоконтроль) усвоения изученного материала в процессе решения задач Ц3: научиться выделять целую часть из неправильной дроби, записывать смешанное число в виде неправильной дроби Ц4: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы |
| 21 | Правильные и не правильные дроби. Смешанные числа | Урок обобщения и систематизации знаний. Математический диктант, работа у доски и в тетрадях | Ц2: контроль усвоения изученного материала Ц3: : решает задачи своего уровня сложности, Ц4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
|
| 22 | Окружность и круг | Урок освоения новых знаний Фронтальная, работа с текстом учебника, работа у доски и в тетрадях | Ц 1: научиться строить окружность (круг) с помощью циркуля, различать окружность и круг на рисунках, показывать и называть радиус, диаметр окружности Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях; |
| 23 | Окружность и круг | Урок формирования и применения знаний, умений и навыков. Индивидуальная работа (карточки-задания), работа у доски | Ц2: использует предписания для решения типов задач своего уровня сложности; Ц3: решает задачи своего уровня сложности, Ц4: уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации |
| 24 | Урок подготовки к контрольной работе | Практикум. Индивидуальная | Ц 2: контроль усвоения изученного материала в процессе изучения нового материала Ц 3: решает задачи своего уровня сложности Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях; Ц 5: выбирает задачи своего уровня сложности , решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы |
| 25 | Контрольная работа №4 «Деление и дроби» | Проверка знаний, индивидуальная работа | Ц : 3, 5: выбирает задачи своего уровня сложности , решает их; |
| 26 | Сложение и вычитание обыкновенных дробей | Урок ознакомления с новым материалом | Ц1: уметь выделять существенную информацию из текстов различных видов |
| 27 | Сложение и вычитание обыкновенных дробей | Урок овладения новыми знаниями, умениями и навыками. Фронтальный опрос, работа в группах, работа у доски | Ц 1: вывести алгоритм сложения (вычитания) дробей с разными знаменателями Ц 2: контроль усвоения изученного материала в процессе изучения нового материала Ц 4: анализирует собственные ошибки с помощью товарища и исправляет их; Ц 3: научиться применять полученный алгоритм при решении практических задач
|
| 28 | Сложение и вычитание обыкновенных дробей | Урок формирования и применения знаний, умений и навыков | Ц2:формировать целевые установки учебной деятельности, выстраивать алгоритм действий Ц3: совершенствовать навыки сложения и вычитания дробей с разными знаменателями Ц4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
|
|
|
|
|
|
| 42 | Умножение и деление обыкновенной дроби на натуральное число | Практикум. Индивидуальная | Ц 2: контроль усвоения изученного материала в процессе изучения нового материала Ц : 3, Ц 5: выбирает задачи своего уровня сложности , решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы |
| 43 | Контрольная работа №5 «Арифметические действия с обыкновенными дробями» | Проверка знаний, индивидуальная работа | Ц : 3, 5: выбирает задачи своего уровня сложности , решает их; |
| 44 | Урок коррекции |
|
|
| Внеурочная самостоятельная деятельность: |
| I. Тематика для подготовки рефератов, выступлений на конференцию, математический вечер, декаду математики и др. (по итогам изучения курса за четверть, за 1-е полугодие, за год) 1) Солнечные часы . 2) Монеты в старину на Руси. 3) Название дробей в старинных книгах. 4) История возникновения дробей, их обозначение. 5) Число пи. 6) Математические фокусы связанные с кругом. 7) Старинные задачи на дроби. II. Тематика долгосрочных проектов по разделу 1) История возникновения дробей, их обозначение. |
§ 6. Примеры реализации целей обучения теме.
| Предмет, класс | Математика, 5 класс | Авторы УМК | И.И.Зубарева, А.Г.Мордкович |
| ФИО учителя, школа | Латышева Наталья Алексеевна, МОУ «Лицей №1», г.Подольск |
| Тема урока | Сложение и вычитание обыкновенных дробей |
| Тип урока | Урок освоения новой учебной информации |
| Цель урока | Ввести правило сложения и вычитания обыкновенных дробей; формировать умение складывать и вычитать обыкновенные дроби |
| Задачи урока | Образовательные: сформировать умение применять алгоритм сложения и вычитания обыкновенных дробей. Развивающие: развивать навыки самоконтроля, взаимоконтроля, умения преодолевать трудности при решении математических задач. Воспитатальные: воспитывать самостоятельность, чувство ответственности, волю и настойчивость при достижении поставленной цели |
| Формирование УУД | регулятивные УУД: умение самостоятельно планировать пути достижения целей, в том числе альтернативные; осуществлять контроль своей деятельности в процессе достижения результата; корректировать свои действия в соответствии с изменяющейся ситуацией; владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности; познавательные УУД: умение самостоятельно планировать пути достижения целей, в том числе альтернативные; осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; осуществлять контроль своей деятельности в процессе достижения результата, коммуникативные УУД: умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе, находить общее решение; формулировать, аргументировать и отстаивать своё мнение; личностные результаты: готовность и способность обучающихся к саморазвитию и личностному самоопределению, способность ставить цели и строить жизненные планы, формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками. |
| Оборудование: | Компьютер, проектор, презентация Microsoft Power Point (приложение), учебник «Математика, 5 класс» И.И.Зубарева, А.Г.Мордкович |
| № этапа | Деятельность учителя | Деятельность ученика | ЦОР | Формы работы | Предметные результаты | УУД |
| 1 | Организационный момент. |
|
| Приветствие, проверка подготовленности к уроку, организация внимания учащихся. | Включаются в деловой ритм урока, настраиваются на продуктивную работу на уроке. |
| Фронтальная работа. | Создание благоприятного психологического настроя на работу. | Организация своей учебной деятельности (регулятивные) Умение слушать, планирование учебного сотрудничества (коммуникативные) |
| 2. | Мотивация к учебной деятельности и постановка целей урока. |
|
| Координирует деятельность учащихся. | Проверяют домашнюю работу (взаимопроверка). Обсуждают спорные и сложные вопросы. |
| Работа в парах, фронтальная работа с классом. | Подготовка к восприятию нового учебного материала | Анализ, сравнение, аналогия, использование знаковой системы, осознанное построение речевого высказывания, подведение под понятие. Умение вести диалог, взаимооценка.
|
| 3. | Повторение и актуализация необходимых знаний |
|
| Организует и контролирует деятельность учащихся
| Устно отвечают на вопросы, Повторяют теорию, решают примеры | Слай-ды 2-5 пре-зен-тации | Фронтальная работа с классом. | Подготовка к восприятию нового учебного материала | Анализ, синтез, аналогия, классификация. Умение слушать и вступать в диалог, оценка действий |
| 4. | Создание проблемной ситуации и формулирование проблемы. |
|
| Организует деятельность учащихся, при необходимости оказывает небольшую помощь. Использует типовые задания. | Работают с учебником, самостоятельно выполняют обучающее задание №420, стр.118 |
| Самостоятельная работа. | Создание проблемной ситуации. | Установление причинно-следственных связей; построение логической цепи рассуждений, подведение под понятие. |
| 5. | Выдвижение гипотез, составление плана действий для решения проблемы, её решение (создание эталона) |
|
| Координирует деятельность учащихся. | Проверяют правильность выполнение №420 (самопроверка) Обсуждают правила сложения и вычитания дробей с одинаковыми знаменателями. Знакомятся с правилами оформления записи при сложении и вычитании дробей. | Слай-ды 6-10. | Индивидуальная (самопроверка). Работа в парах. Фронтальная работа с классом. | Формулировка правил сложения и вычитания дробей. Алгоритм сложения и вычитания дробей. Запись алгоритма в буквенной форме. | Выдвижение гипотез и их обоснование, подведение под понятие. Умение слушать и вступать в диалог, оценка действий (своих и товарищей).
|
|
| ФИЗКУЛЬТМИНУТКА. (Слайд 11). |
| 6. | Первичное закрепление (действие в форме громкой, внешней речи) |
|
| Организует и контролирует деятельность учащихся. | Решают у доски с объяснением и в тетрадях №423, стр.119. | Слайд 12. | Работа у доски и в тетрадях. | Первичное закрепление применения алгоритма сложения и вычитания дробей с одинаковыми знаменателями. | Анализ, контроль; коррекция; оценка, оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли |
| 7. | Самостоятельная работа (действие в форме внутренней речи) |
|
| Организует и контролирует деятельность учащихся. | Самостоятельно решают в тетрадях №424, стр.119. Двое учащихся решают задание (по два примера) на откидной доске. | Слайд 12. | Самостоятельная работа в тетрадях и у доски. Проверка выполненного задания. | Закрепление навыка сложения и вычитания дробей с одинаковыми знаменателями. | Составление и реализация плана деятельности при освоении учебной информации; контроль усвоения учебной информации; оценивание результатов выполненной деятельности. |
| 8. | Включение изученной учебной информации в систему известных знаний. |
|
| Предлагает для решения типовые задания по теме урока. Координирует и контролирует деятельность учащихся, оказывает консультацион-ную помощь. | Решают предложенные задания из учебника: №426, 428. |
| Работа в парах. | Вычитание обыкновенной дроби из единицы. Применение этого умения при решении простейших задач. | Выбор эффективных способов решения задач в зависимости от конкретных условий; 4 управление поведением партнёра – контроль, коррекция, оценка действий партнёра |
| 9. | Рефлексия деятельности (соотнесение результатов с поставленными целями урока) |
|
| Мотивирует учащихся на подведение итогов урока Выявляет уровень усвоения изученного материала. Комментирует домашнее задание. Выставляет оценки за урок.
| Обобщают изученный материал. Делают вывод. Оценивают свою работу. Записывают домашнее задание.
| Слай-ды 13-15. | Фронтальная работа. | Подведение итогов урока. | Оценивание результатов выполненной деятельности, самоконтроль и самооценка процесса и результатов деятельности; построение речевых высказываний. |
Ход урока.
«Считай несчастливым тот день или тот час,
в который ты не усвоил ничего нового
и ничего не прибавил к своему образованию»
Ян Амос Коменский
1.Организационны момент.
- Здравствуйте ребята! Посмотрите друг на друга, улыбнитесь, желаю вам успешной работы! Садитесь.
2. Мотивация к учебной деятельности и постановка целей урока.
- Проверка домашнего задания. ( Учащиеся проверяют домашние задания друг друга, выставляют оценки карандашом.)
3. Повторение и актуализация необходимых знаний.
На слайде 2 записаны дроби и стихотворение с пропусками.
Каждый может за версту
Видеть дробную ………(черту)
Над чертой ……… . Знайте! (числитель)
Под чертою …………. . (знаменатель)
Дробь такую непременно
Надо звать ……………. .(обыкновенной)
На слайде 3 изображены числа

Вопросы:
- Какие числа перед вами? (Целые и дробные)
- Прочитайте дробные числа. Назовите числитель и знаменатель каждой дроби.
- Какие действия мы научились выполнять с дробными числами? (Сокращать, приводить к новому знаменателю, правильные и неправильные дроби, выделять целую часть неправильной дроби, сравнивать дроби с одинаковыми знаменателями…)
Слайд 4.
Приведите числа к знаменателю 20:
Каким свойством вы при этом пользовались?
Слайд 5.
Сравните числа (с обоснованием):
.
Слайд 6.
Выделите целую часть.
4. Создание проблемной ситуации и формулирование проблемы.
- Мы многое уже знаем об обыкновенных дробях. А какие арифметические действия мы пока не выполняли с дробями? (сложение, вычитание, умножение и деление)
- Сегодня мы научимся складывать и вычитать обыкновенные дроби с одинаковыми знаменателями.
- Выполните в тетрадях №420 (стр.118 учебника).
5. Выдвижение гипотез, составление плана действий для решения проблемы, её решение (создание эталона).
Слайд 7. (Источник слайдов 7 – 9 http://school-collection.edu.ru/catalog/rubr/c27e8cd5-c3e0-4724-ad9d-737d78c0d95f/113794/?)
- Проверьте правильность выполнения задания №420.(самопроверка)
- Выполняя последние задания, вам пришлось складывать и вычитать дроби с одинаковыми знаменателями. Попробуйте сформулировать правила для сложения и вычитания обыкновенных дробей с одинаковыми знаменателями.
(Ответы учащихся сначала в парах, затем обсуждение в классе)
Слайд 8. (правила)
- Нам нужно правильно записывать примеры на сложение и вычитание дробей.
Слайд 9.
- Проследите как правильно оформлять записи в тетрадях при решении примеров на сложение и вычитание дробей.
- Запишите решение самостоятельно, а затем проверьте себя.
 .
.
- А как записать правила сложения и вычитания обыкновенных дробей с одинаковыми знаменателями на математическом языке (формулы)?
Слайд 10.
- Мы молодцы! Работали продуктивно и дружно. Пришло время немного отдохнуть и размяться.
Слайд 11.
ФИЗКУЛЬТМИНУТКА.
Руки в боки, руки – шире
Раз, два, три, четыре.
Сейчас попрыгать мы решили.
Раз, два, три, четыре.
Потянулись - выше, выше…
Приседаем – ниже, ниже…
Встали – присели…
Встали – присели…
А теперь за парты сели.
Слайд 12.
6. Первичное закрепление (действие в форме громкой, внешней речи).
Выполнение №423, стр.119. У доски работают ученики (по желанию), решают по одному примеру с объяснением и проговариванием алгоритма действий. Остальные – выполняют задание в тетрадях.
7. Самостоятельная работа (действие в форме внутренней речи).
Учащиеся решают самостоятельно №424, стр.119 в тетрадях. Двое учащихся решают задания на откидной доске. Затем проверяют правильность выполнения задания и выполнения записей в тетрадях и на доске.
8. Включение изученной учебной информации в систему известных знаний.
Решение учащимися в парах №426, 428, стр.119. Затем обсуждается и проверяется решение.
Слайды 13-16.
9. Рефлексия деятельности (соотнесение результатов с поставленными целями урока).
- Какую тему мы сегодня изучали? (сложение и вычитание дробей с одинаковыми знаменателями)
- А какие задачи мы для этого ставили? (научиться складывать и вычитать дроби с одинаковыми знаменателями)
– Наши задачи выполнены? (да)
Домашнее задание: стр. 119-120,
1 уровень: № 425, 429,433,
2 уровень: № 427, 430,
3 уровень: №427, 430, 431.
–Выставление оценок за урок
- За что ты сегодня можешь себя похвалить?
- Что тебе удалось сегодня на уроке?.
- Над чем надо еще поработать?
ЗАКЛЮЧЕНИЕ
Математика - важнейшая наука, созданная нашей цивилизацией и сопро-
вождающая ее на всех этапах развития. Вся современная наука: физика и хи-
мия, биология и экономика, лингвистика и социология не только использует
математические методы, но и строится по математическим законам. Путь в современную науку и технику, просто в современную жизнь лежит через математику. Этот элемент научного знания является важнейшей частью математического образования.
Термин универсальные учебные действия означает способность субъек-
та к саморазвитию через сознательное и активное присвоение социального
опыта, совокупность способов действия учащегося, а также связанных с ними навыков учебной работы, обеспечивающих его способность к самостоятельному усвоению новых знаний и умений. Таким образом, актуальной становится проблема создания механизмов формирования УУД: для чего необходимо выявлять теоретические основы обучения каждой теме, связанные с реализацией ФГОС ООО; выполнять отбор средств обучения теме, в том числе средства ИКТ; разрабатывать таблицы целей и карты обучения теме.
Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; тестирование учащихся, проведение опытной проверки.
Образование должно развиваться, так как развивается мир, страна, каждый из нас, и тогда школа сможет выполнить заказ государства
по воспитанию и развитию подрастающего поколения.
Список литературы
А) Основной
Приоритетный национальный проект «Образование» - http://mon.gov.ru/pro/pnpo
Национальная образовательная инициатива «Наша новая школа» - http://mon.gov.ru/dok/akt/6591
Федеральная целевая программа развития образования на 2011-2015 годы - http://mon.gov.ru/press/news/8286
Федеральный государственный образовательный стандарт основного общего образования. – М.: Просвещение, 2011- 48с.
Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. - М.: Просвещение, 2010. - 159 с.
Данилюк А.Я., Кондаков А.М., Тишков В.А. Концепция духовно-нравственного развития и воспитания личности гражданина России. – М.: Просвещение, 2009. – 24 с. (Стандарты второго поколения) – 24с.
Постановление Главного государственного санитарного врача Российской Федерации от 29 декабря 2010 г. №189 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (Санитарно-эпидемиологические правила и нормативы СанПиН 2.4.2. 2621-10).
Система гигиенических требований к условиям реализации основной образовательной программы основного общего образования - http://standart.edu.ru
Асмолов А.Г. Системно-деятельностный подход к разработке стандартов нового поколения. // Педагогика.- 2009.-№4.- С.18-22.
Формирование УУД в основной школе: от действия к мысли. Система заданий. Пособие для учителя. // Под ред. Асмолова А.Г. – М.: Просвещение, 2010.
Примерная основная образовательная программа образовательного учреждения. Основная школа. – М.: Просвещение, 2011 – 67 с.
Боженкова Л.И. Алгебра в схемах, таблицах, алгоритмах: Учебные материалы. Калуга: КГПУ, 2012.
Иванов Д.А., Митрофанов К.Г., Соколова О.В. Компетентностный подход в образовании. – М.: АПКиППРО, 2005.
В) Дополнительный
Александрова Н.В. История математических терминов, понятий, обозначений. – М.: ЛКИ, 2007. – 248 с.
Гнеденко Б.В. Очерки по истории математики в России. - М.: ЛКИ, 2009. – 296 с.
Давыдов В.В. Теория развивающего обучения. М.: Педагогика, 1996.
Дистанционные образовательные технологии: проектирование и реализация учебных курсов. / Под общ.ред. М.Б.Лебедевой. – СПб.: БХВ-Петербург, 2010.
Примерные программы внеурочной деятельности / Под ред. В.А.Горского. – М.: Просвещение, 2010.
Программа внеурочной деятельности. Познавательная деятельность. Проблемно-ценностное общение. М.: Просвещение, 2011. – 96 с. (Стандарты второго поколения).
Соболева О.В. Обучение пониманию текста: учебная книга – учитель- ученик // Психологическая наука и образование. 2006, № 1.
Шуба М.Ю. Учим творчески мыслить на уроках математики. - М.: Просвещение, 2012. – 218 с. (Работаем по новым стандартам).
Журналы «Математика в школе».
Журналы «Педагогика».
Журналы «Стандарты и мониторинг образования».
С) Интернет-ресурсы
http://standart.edu.ru – ФГОС общего образования и разработанные к ним документы.
http://school-collection.edu.ru/ - каталог Единой коллекции цифровых образовательных ресурсов.
http://fcior.edu.ru - каталог электронных образовательных ресурсов ФЦ.
http://window.edu.ru – электронные образовательные ресурсы.
http://katalog.iot.ru – электронные образовательные ресурсы.
http://www.it-n.ru/ - «Сеть творческих учителей».
http://www.ict.edu.ru - портал "Информационно-коммуникационные технологии в образовании".
http://www.metodist.lbz.ru/content/videoafisha.php - видеолекции авторов УМК по школьной математике.
http://inf.1september.ru - газета «Математика» Издательского дома «Первое сентября».
www.school.edu.ru/ Центральный образовательный портал. Содержит нормативные документы Министерства образования и науки, стандарты, информацию о проведении экспериментов.
http://fcior.edu.ru Федеральный центр информационно-образовательных ресурсов
http://www.ucheba.com/ Портал «Учеба».
http://www.edu.yar.ru/russian/pedbank Банк педагогического опыта.
http://www.mccme.ru/mmmf-lectures/books Популярные лекции по математике.
http://www.comp-science.narod.ru/ Дидактические материалы по информатике и математике.
http://www.mccme.ru/ МЦНМО. Математические праздники, олимпиады, базы данных задач с решениями, математическое образование в документах, статьях, публикациях, математические игры и др.
Приложения
Приложения №1-8. Средства помощи при обучении теме «Обыкновенные дроби».
Приложение № 1
Виды математических выражений
| № п/п | Название вида выражения с - результат | Символьная запись | Компоненты | Название действий |
| 
| 
|
| 1 | Частное (отношение чисел) |  : : 
| делимое | делитель | деление |
| 2 | Дробь (отношение чисел) |  = с = с
| числитель | знаменатель | деление |
Приложение № 2
Действия с дробями:
.
Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
Если знаменатели данных дробей разные, то дроби нужно сначала привести к общему знаменателю, а потом поступить, как описано выше.
Вычитание. Если две дроби имеют одинаковые знаменатели, то
Если знаменатели данных дробей различны, то сперва приводят дроби к общему знаменателю, а потом вычитают их по вышеприведённой формуле.
Приложение № 3
Окружность и круг:


Окружность
Окружность делит плоскость на две части. Ту часть плоскости, которая лежит внутри окружности (вместе с самой окружностью), называют кругом.
3. Точку О – центр и круга, и окружности.
4. Все радиусы окружности равны друг другу.
5. Отрезок АВ – диаметром окружности (и круга).
6. Диаметр окружности вдвое длиннее ее радиуса.
7. Диаметр делит круг на два полукруга, а окружность — на две полуокружности.
8. А В - дуга окружности, а точки А и В — концами этих дуг.
Приложение № 4
Обыкновенная дробь  называется правильной, если её числитель меньше её знаменателя, то есть m n.
называется правильной, если её числитель меньше её знаменателя, то есть m n.
Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m  n
n
Приложение № 5
Предписание выделения целой части из неправильной дроби:
разделить с остатком числитель и знаменатель;
неполное частное будет целой частью;
остаток (если он есть) дает числитель, а делитель – знаменатель дробной части.
Приложение № 6
Предписание для сравнения дробей с одинаковыми знаменателями:
конец
Приложение № 7
Предписание представления смешанной дроби в виде неправильной дроби:
умножить его целую часть на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Приложение № 8
Предписание при сложении (и вычитании) чисел в смешанной записи:
целые части дроби складываются (вычитаются) отдельно;
дробные части дроби складываются (вычитаются) отдельно;
Если при сложении смешанных чисел в их дробной части получается неправильная дробь, то из дробной части выделяют целую часть и добавляют ее к уже имеющейся целой части.
Пример:
 .
.
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Пример:
Короче:  .
.
Если вычитают смешанную дробь или дробь их натурального числа, поступают так:
Пример:
1)  . 2)
. 2) 

 Получите свидетельство
Получите свидетельство Вход
Вход




 называют обыкновенными дробями
называют обыкновенными дробями - числитель
- числитель -знаменатель
-знаменатель
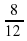 ; б)
; б)  .
.  ; б)
; б)  ; в)
; в) 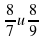 .
.  книги. Сколько страниц в книге?
книги. Сколько страниц в книге?  которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами.
которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами.  ; б) 23
; б) 23 .
.  ; б)
; б)  .
. 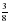 диаметра первой. Начертите эти окружности.
диаметра первой. Начертите эти окружности.  собственной скорости катера?
собственной скорости катера? 








 Реализация требований ФГОС ООО при обучении теме: “Обыкновенные дроби” (0.16 MB)
Реализация требований ФГОС ООО при обучении теме: “Обыкновенные дроби” (0.16 MB)
 0
0 9344
9344 201
201 Нравится
0
Нравится
0




