Способы вычисление площади многоугольников.
А) Подсчет клеток
Нужнопосчитатьколичествополныхклетоквнутриданнойфигуры.
Дополнитьнеполныеклеткидругдругомдополныхклеток.
Чтобы найти площадь фигуры надо найти сумму полных клеток.
 Решение:
Решение:
Посчитаем количество клеток внутри закрашенной области: их 11.
 Решение:
Решение:
Посчитаем количество клеток внутри закрашенной области: их 18

Б) Использование основных формул планиметрии

Задача 1.Найдем площадь параллелограмма ADCB, а FDCB - равновеликий ему прямоугольник. Из курса начальной школы мы знаем, что площадь прямоугольниканаходится по формуле:
S=a*b,
гдеа и b – длина и ширина прямоугольника
В параллелограмме ADCBFD- это высота, а DC – длина. Следовательно, площадь параллелограмма: SADCB= FD*DC, SADCB=5*7=35.

Задача 2. В общем случае площадь параллелограмманаходится по формуле (рисунок 4а):
S=a*h,
где а- основание, а h- высота параллелограмма.

Задача 3.Еще раз обратимся к формуле площади прямоугольника S=a*b,где а и b – стороны прямоугольника, тогда площадь прямоугольного треугольника найдем так:S= 3*3:2=4,5
В общем случае, площадь прямоугольного треугольника, находится по формуле:
S=(a*b):2,где а и b – катеты.
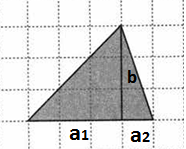
Задача 4.Площадь произвольного треугольника найдем как сумму площадей двух прямоугольных треугольников. Площадь большего треугольника находится так:Sб=a1*b:2=(3*3):2=4,5, меньшего треугольника Sм=a2*b:2=(1*3):2=1,5А площадь целого треугольника S=S1+S2=4,5+1,5=6

C другой стороны можно заметить, что катеты а1 и а2большего и меньшего прямоугольных треугольников составляют основание исходноготреугольника, катет b в исходном треугольнике является высотой h.Таким образом основание а=а1 +а2, высота h=b. Тогда, площадь данного треугольника S=(4*3):2=6
В) Разбиение многоугольника на части
Задача1.Найтиплощадьпрямоугольника,изображеннойнаклетчатойбумаге сразмеромклетки1смх1см.Ответдайте вквадратныхсантиметрах.


Решение.РазобьемданныйпрямоугольникАВСДнадватреугольникаАВСиВСД. Сторона у них общая и равна 5 см. Высоты, опущенные на эту сторону,равны2см.Так как площадь треугольника равна половине произведения стороны навысоту, опушенную на эту сторону, то площадь каждоготреугольника равна5кв.см.и,следовательно,площадьпрямоугольника будетравна10 см2.

 Задача 2. Найти площадь многоугольника, изображенного на клетчатойбумаге,считаястороныквадратныхклеток равными1.
Задача 2. Найти площадь многоугольника, изображенного на клетчатойбумаге,считаястороныквадратныхклеток равными1.
Решение. Разобьем фигуру на треугольники и прямоугольник как показанона рис (можно разбить по-другому). Площадь прямоугольного треугольникаравнаполовинепроизведениякатетов,следовательно,площадиихраны6,2,и3ед2,площадьпрямоугольникаравна2х1=2(ед2).Складываяплощади,
полученных фигур 6 + 2 +3 + 2, получим площадь заданнойфигуры 11кв.ед.Способ разбиения на части подходит для любого многоугольника,но он трудоемкий.
Г) Достраивание многоугольника до прямоугольника
Задача1. Найдитеплощадьчетырехугольника,изображенногонаклетчатойбумаге с размеромклетки1 см х1см.
 Решение.Опишемоколонеёпрямоугольник.
Решение.Опишемоколонеёпрямоугольник.
Изплощадипрямоугольника(вданномслучаеэтоквадрат)вычтемплощади полученныхпростыхфигур:
 S= Sпр. –S1–S2–S3–S4=4*4–½*1*4-1/2*3*3-
S= Sпр. –S1–S2–S3–S4=4*4–½*1*4-1/2*3*3-
½*2*2–(1+2)/2*2=4.5(кв.см.)
З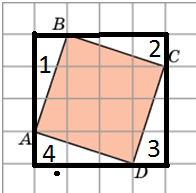 адача 2.Найдём площадь фигуры АВСD.
адача 2.Найдём площадь фигуры АВСD.
Решение. Опишем около нее прямоугольник, точнее квадрат.
Из площади квадрата вычтем площади полученных фигур (1, 2, 3 и 4):S = Sкв – S1 – S2 – S3 – S4 == 4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = =10.
З адача 3.Найдём площадь фигуры АВСD.
адача 3.Найдём площадь фигуры АВСD.
Решение. Опишем около фигуры АВСD квадрат.Из площади квадрата вычтем площади полученных фигур (1, 2 и 3):
S=Sкв–S1–S2–S3=4∙4–(4∙4):2–(2∙1):2–(2∙1):2 =16-8–1–1=6
ФормулаПика.
Историческая справка
Формула Пика была открыта австрийским математиком Георгом Пиком в 1899 году. (см. приложение 1). Эта формула для нахождения площади многоугольника с вершинами, расположенными в узлах клетки. Узлами называются точки пересечения вертикальных и горизонтальных линий. Формула Пика связывает площадь многоугольника с количеством узлов, лежащих внутри и на границе многоугольника.
формула для нахождения площадей фигур на решётчатой бумаге.

Формула Пика:
S=В+Г/2−1,
где В—количество внутренних точек (узлов) многоугольника,
Г— количество граничных точек (узлов) многоугольника. Формула Пика работает только для многоугольников без дырок, всевершины которых попадают в узлы сетки.
Использование формулы для нахождения площадей фигур на решётчатой бумаге.
|
|
Здесь В = 12 (внутренние узлы), Г=4 (граничные узлы), поэтому S=12+4/2-1=13. |
|
|
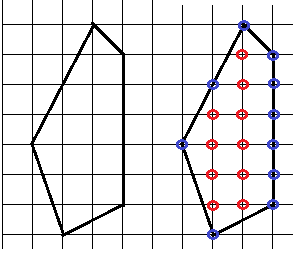
Здесь В = 4, Г=6, поэтому S=4+6/2-1=8.
|
|
|
Здесь В = 10, Г=10, поэтому S=10+10/2-1=14.
|
Задачи из сборников по подготовке к ОГЭ.
Мы убедились, что возможны различные способы нахождения фигур на клетчатой бумаге. Можно находить площади фигур, используя формулы геометрии (но для этого надо знать эти формулы и уметь ими пользоваться). Можно находить площади частей фигур, а затем уже площадь целой фигуры. Можно дополнять фигуру до прямоугольника и из него вычитать «лишние» части (в некоторых случаях эти способы применить очень трудно, да и вычисления занимают много времени). А на экзамене по математике в 9-м и в 11-м классе каждая минута дорога!
Поможет ли формула Пика при выполнении аналогичных заданий из вариантов контрольно-измерительных материалов ОГЭ по математике?
З адача 1. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
адача 1. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см ![]() 1 см.
1 см.
В ычисляем, используя формулу площади трапеции, получаем,что
ычисляем, используя формулу площади трапеции, получаем,что
Вычисляем, используя формулу Пика, внутренних 11 узлов, граничных – 13, получаем:
В ывод: в данном случае лучше использовать формулу площади трапеции.
ывод: в данном случае лучше использовать формулу площади трапеции.
З адача 2. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
адача 2. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см ![]() 1 см.
1 см.
Вычисляем, используя способ нахождения площади фигуры как части площади прямоугольника:
Sпр=7*6=42,
Sтр1=6*6:2=18,
Sтр2=2*2:2=2,
Sтр3=4*1:2=2,
Sф=42-(18+2+2)=20 см2.
Вычисляем, используя формулу Пика 14+14/2-1=20см2.
Вывод: в данном случае лучше использовать формулу Пика.
З адача 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
адача 3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см ![]() 1 см.
1 см.
Вычисляем, используя формулу Пика: В=6, Г= 4
S=6+4/2-1=7см2.
В данной задаче любой другой способ приведет к громоздким вычислениям.
Еще решения задач представлению в приложении 2
Рассмотрим на одном примере вычислениеплощадимногоугольникаразнымиспособами (см. приложение3).Решая этимиспособами, я получила один и тот же ответ. Значит,площадьнезависитотспособа.Подтвердиласьигипотеза:площадьмногоугольника,изображенногонаклетчатойбумаге,можновычислитьразными способами и площадь не зависит от способа вычислений. Определитьплощадь помогала клетка. Следует заметить, что с помощью формулы Пика ябыстроилегковычислилаплощадь.

 Получите свидетельство
Получите свидетельство Вход
Вход













 Способы вычисления площадей многоугольников (2.01 MB)
Способы вычисления площадей многоугольников (2.01 MB)
 0
0 666
666 11
11 Нравится
0
Нравится
0








