Получите свидетельство
Вход
Способы решения линейных и квадратных неравенств
Линейные неравенства - это неравенства вида ax+b0 (где a и b – некоторые действительные числа, неравные нулю, и они решаются двумя способами: эквивалентными преобразованиями либо с помощью графика функции.
Правила линейных неравенств
Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.
2x − 3 6 ⇒ 2x 6 + 3 ⇒ 2x 9.
Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.
Умножим обе части на пять 2x 9 ⇒ 10x 45.
Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.
Разделим обе части на минус два 2x 9 ⇒ 2x : (–2) 9 : (–2) ⇒ –x
Равносильные преобразования
Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.
Алгоритм решения ax + b
перенесем число b в правую часть с противоположным знаком,
получим равносильное: ax
произведем деление обеих частей на число не равное нулю.
Когда a положительное, то знак неравенства остается без изменений, если a — отрицательное, знак меняется на противоположный.
Рассмотрим пример: 4x + 16 ≤ 0.
Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.
Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
Произведем деление обеих частей на 4. Не меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4.
Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.
Ответ: x ≤ −4 или числовой промежуток (−∞, −4].
При решении ax + b
Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b
Числовое неравенство вида b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.
Рассмотрим пример: 0x + 5 0.
Данное неравенство 0x + 5 0 может принимать любое значение x.
Получается верное числовое неравенство 5 0. Значит его решением может быть любое число.
Ответ: промежуток (− ∞ , + ∞).
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов заключается в следующем:
вводим функцию y = ax + b;
ищем нули для разбиения области определения на промежутки;
отмечаем полученные корни на координатной прямой;
определяем знаки и отмечаем их на интервалах.
Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:
найдем нули функции y = ax + b для решения уравнения ax + b = 0.
Если a ≠ 0, тогда решением будет единственный корень — х₀;
начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
определим знаки функции y = ax + b на промежутках.
Для этого найдем значения функции в точках на промежутке;
если решение неравенства со знаками или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если
Рассмотрим пример: −6x + 12 0.
Как решаем:
В соответствии с алгоритмом, сначала найдем корень уравнения
−6x+12=0,
−6x = −12,
x = 2.
+ 2 -
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6*1 + 12 = 6, 6 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6*3 + 12 = − 6, − 6
Линейные неравенства эффективно решаются путем выбора интервалов, на которых функция сохраняет знак, т.е. до корня и после корня. Решением линейного неравенства, как правило, является луч.
|x|— расстояние на числовой прямой от 0 до точки a.
|u|=u −− u≥0
|u|=−u −− u≤0
|u|=|v| −− v2=u2
|x| −a Система
|x|≤a −− −a≤x≤a Система
|x|a −−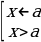 
Совокупность
|x|≥a −−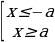 
Совокупность
Например:
Решить неравенство |3+x|≥|x|.
Решение. |3+x|≥|x|
(3+x)2≥x2
x2+6x+9≥x2
6x≥−9
x≥−1,5
Ответ: [−1,5;+∞)
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
во время решения ax + b
во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.
Рассмотрим пример: −5x−√30.
Как решаем
Так как коэффициент при x отрицательный, данная прямая является убывающей.
Координаты точки пересечения с Ох равны (−√3:5; 0).
Неравенство имеет знак , значит нужно обратить внимание на промежуток выше оси Ох.
Поэтому открытый числовой луч (−∞, −√3:5) будет решением.
Ответ: (−∞, −√3:5) или x
Решить неравенство 2х+10
Построим график функции. Графиком является прямая, она пересекает ось Оy в точке 1, ось Оx в точке -1/2. Корень функции разбивает ось Оx на два различных промежутка. На первом промежутке функция отрицательна, на втором – положительна.
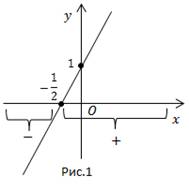
Этого достаточно, чтобы решить линейное неравенство.
Ответ: 
Решение линейных неравенств с параметром
Линейные неравенства с параметром имеют вид ax + b 0, где a и b – параметры. Для их решения:
1. Определяем области, где параметр a принимает значения, равные нулю.
2. Рассматриваем случаи, когда a 0 и a
Пример решения линейного неравенства с параметром: (k + 2)x − 3 0.
Решение:
1. k + 2 = 0 → k = −2.
2. k + 2 0 → k −2.
3. k + 2
Пример 1.
Решить неравенство |x + 5|
Решение.
Строим графики функций у = |x + 5| и у = bx (рис. 2). Решением неравенства будут те значения переменной х, при которых график функции у = |x + 5| будет находиться ниже графика функции у = bx.
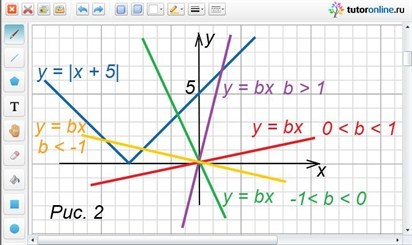
На рисунке видно:
1) При b 1 прямые пересекаются. Абсцисса точки пересечения графиков этих функций есть решение уравнения х + 5 = bx, откуда х = 5/(b – 1). График у = bx находится выше при х из интервала (5/(b – 1); +∞), значит это множество и есть решение неравенства.
2) Аналогично находим, что при -1
3) При b ≤ -1 x € (-∞; 5/(b – 1)).
4) При 0 ≤ b ≤ 1 графики не пересекаются, а значит, и решений у неравенства нет.
Ответ: x € (-∞; 5/(b – 1)) при b ≤ -1; x € (-5/(b + 1); 5/(b – 1)) при -1
решений нет при 0 ≤ b ≤ 1; x € (5/(b – 1); +∞) при b 1.
Квадратные неравенства
Решение квадратных неравенств ax2 + bx + c 0 (
1 Вводим соответствующую функцию y= ax2 + bx + c
2 Определяем направление ветвей параболы y= ax2 + bx + c (при а0 ветви направлены вверх; при а
3 Находим нули функции, т.е. решаем уравнение ax2 + bx + c =0.
4 Если уравнение имеет корни, то отмечаем корни на координатной прямой и схематически рисуем параболу в соответствии с направлением ветвей. Если уравнение не имеет корней, то схематически рисуем параболу в соответствии с направлением ветвей.
5 Находим решение неравенства с учётом смысла знака неравенства.
Решение квадратных неравенств, в зависимости от дискриминанта соответствующего квадратного уравнения, разбивается на 3 случая:
1) D 0; 2) D = 0; 3) D
Квадратичная функция в общем виде, D0
Функция имеет вид y= ax2 + bx + c, D0, значит, корни квадратного трехчлена различны, x1≠x2.
Графиком квадратичной функции является парабола, пересекающая ось Ox в точках с абсциссами x1≠x2, a0, ветви параболы направлены вверх.
Вне интервала корней функция имеет положительный знак, внутри интервала корней – отрицательный.
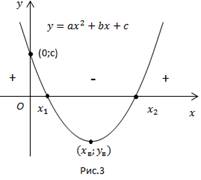
Что можно сказать о функции, если DПрежде всего, что она разлагается на линейные множители: y= ax2 + bx + c = a (x-x1)(x-x2).
Также для нее справедлива теорема Виета:
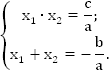
Найдем координаты вершины параболы.
Для квадратичной функции есть два возможных варианта неравенств:
Множество значений функции – луч от yв в положительном направлении. 
Точка пересечения с осью Оy – т. (0;с).
Квадратичная функция в общем виде, D=0
2. 
Как и в предыдущем случае, многочлен раскладывается на множители.
График функции – парабола, ветви направлены вверх.
Парабола касается оси ox в одной точке, которая и является вершиной параболы.
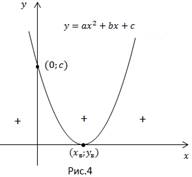
Рассмотрим возможные варианты неравенств:
Множество значений функции: 
График функции пересекается с осью Оy в т. (0;с).
Квадратичная функция в общем виде, D
3. 
Рассмотрим функцию y= ax2 + bx + c.
D
Найдем координаты вершины: 
Схематически изобразим график – параболу, ветви направлены вверх.
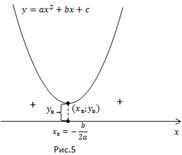
В этом случае часто допускается стандартная ошибка – нет корней, значит, нет решений. Корней нет у квадратного уравнения, а решением неравенства является любое действительное число.
Множество значений функции 
Для более глубокого рассмотрения рекомендуется самостоятельно изучить случаи, когда 
1. 
2. 
3. 
Пример:
2x2+x−3≥0
2x2+x−3=0
Найдём корни этого уравнения:
x1=−32; x2=1
Отметим корни на оси Ox и схематично покажем ориентацию ветвей параболы («вверх» или «вниз»)
Расставим на оси знаки, соответствующие знаку квадратичной функции: там где парабола выше оси, ставим «+», а там где ниже – «—».
Выписываем интервал(ы), соответствующий(ие) «+» или «—», в зависимости от знака неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое — не входят.
x∈(−∞;−32]∪[1;+∞)
Решение квадратных неравенств с параметромКвадратные неравенства с параметром имеют вид aх² + bx + c 0, где a, b и c – параметры. Для их решения используем дискриминант:
1. Вычисляем дискриминант D = b2 − 4ac.
2. Определяем знаки коэффициентов и дискриминанта.
Пример решения квадратного неравенства с параметром:
х² + (a − 1)x + a2 − 1
Решение:
1. D = (a−1)² − 4(a² − 1) = 1 − 2a − 3a².
2. Анализируем знаки дискриминанта и коэффициентов.
Решение систем неравенств с параметромСистемы неравенств с параметром решаются путем нахождения пересечения решений каждого неравенства в системе.
Пример решения системы неравенств с параметром:
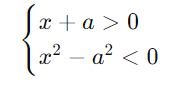
Решение:
Решаем первое неравенство: x −a.
Решаем второе неравенство: −a
Находим пересечение решений: −a
Пример:
Решить неравенство 5х – а ax + 3.
Решение.
Для начала преобразуем исходное неравенство: 5х – ах a + 3,
вынесем за скобки х в левой части неравенства: (5 – а)х a + 3.
Теперь рассмотрим возможные случаи для параметра а:
Если a 5, то x
Если а = 5, то решений нет.
Если а (а + 3) / (5 – а).
Данное решение и будет являться ответом неравенства.
Исследуем полученную систему на интервалах и в точках (рис. 1):
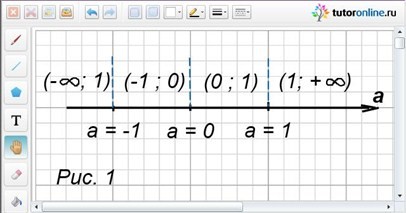
При а ≤ -1 х € (-∞; 1/(а – 1)].
При -1
При а = 0 x = -1.
При 0
В данных пояснениях использовалась система неравенств. Это значит, что все условия выполняются одновременно. При записи неравенства объединяются фигурной скобкой (можно прочитать её как союз И): 
.
В случаях, когда используется совокупность (можно прочитать её как союз ИЛИ):
, должно выполняться хотя бы одно из условий
Сходство между системой и совокупностью неравенств с одной переменной заключается в том, что оба понятия представляют собой несколько неравенств с одной переменной, объединённых для решения определённой задачи.
Различия заключаются в том, что система неравенств требует найти все такие значения переменной, каждое из которых является частным решением всех заданных неравенств. Решение системы — пересечение решений неравенств, входящих в систему. Совокупность неравенств, в свою очередь, предполагает нахождение всех таких значений переменной, каждое из которых является решением хотя бы одного из заданных неравенств. Решение совокупности — объединение решений неравенств, входящих в совокупность.
Также система неравенств записывается с помощью фигурной скобки, а совокупность — с помощью квадратной.
Как их решать? Нужно по отдельности решить каждое из неравенств, а дальше всё зависит от того, система перед нами или совокупность. Если это система, должны выполняться все условия.
Если это совокупность, то нам подойдут все значения, которые являются решениями хотя бы одного неравенства.
Способы решения уравнений и неравенств (180.76 KB)
0
204
1
Нравится
0
