Сопряжение линий

Инженерная графика — это дисциплина, без которой невозможно представить современное общество.

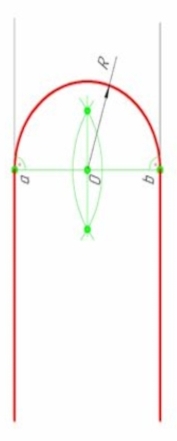
Н екоторые аспекты этой дисциплины постоянно окружают нас в нашей повседневной жизни. Один из таких аспектов — сопряжение линий — прием, позволяющий плавно соединять различные прямые и окружности между собой. Является одним из простейших приемов в инженерном деле и применяется человечеством с древних времен. Самым известным подтверждением этого является циркульная арка в архитектуре Древнего Рима.

Большую роль в систематизации сопряжения линий сыграл Гаспар Монж — французский математик и человек, сделавший большой вклад в развитие геометрии и инженерной графики.

В своей работе “Начертательная геометрия” он выработал геометрические принципы, лежащие в основе сопряжения:

1. Условия касания линии к окружности (или двух окружностей).

2. Методы построения точек касания.

3. Правила выбора центра сопрягающей окружности.

Благодаря его работе сопряжение линий стало более доступным для инженеров.

Перед разбором основных принципов сопряжения линий, следует рассмотреть ключевые понятия этой темы:

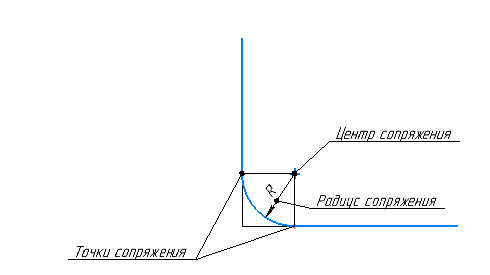
• Центр сопряжения — точка, из которой циркулем будет проведена дуга плавного перехода одной линии к другой.

• Радиус сопряжения — радиус дуги сопряжения, с помощью которой происходит сопряжение.

• Точка сопряжения — общая точка сопрягаемых линий, в которой происходит плавный переход линий.

1. Сопряжение двух прямых линий, параллельных друг другу.

Выполняют в следующей последовательности: от первой прямой, на расстоянии, равном радиусу сопряжения, проводят дополнительную прямую. Из точки, перпендикулярной к концам сопрягаемых прямых, проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит две параллельные прямые.

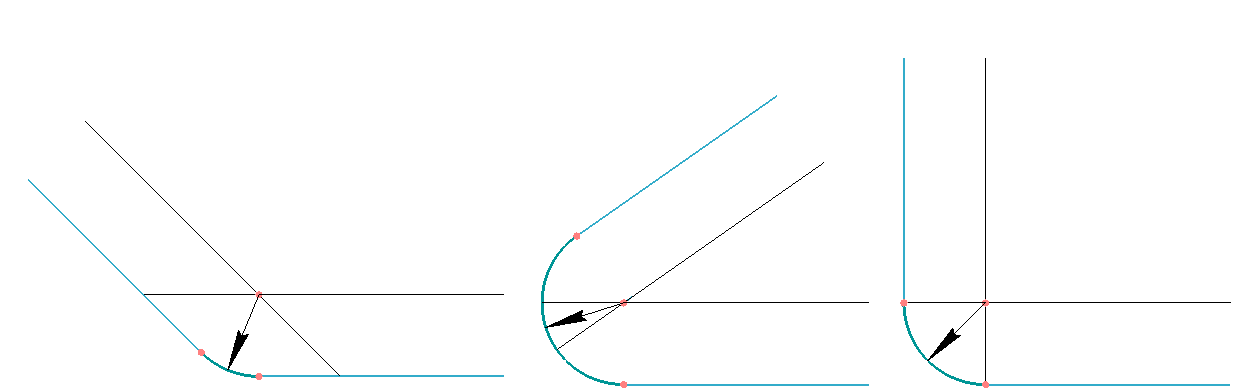
1. Сопряжение двух прямых линий, расположенных под любыми углами.

Алгоритм выполнения: от первой прямой, на расстоянии, равном радиусу сопряжения, проводят дополнительную прямую. Аналогично проводят дополнительную прямую от второй прямой. Точка пересечения дополнительных прямых является центром сопряжения. Из получившейся точки проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит обе прямые.

1. Сопряжение дуги окружности с прямой.

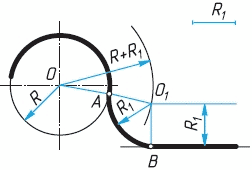Последовательность выполнения: от прямой, на расстоянии, равном радиусу сопряжения, проводят дополнительную прямую. Из центра окружности проводят дугу, радиус которой равен сумме радиуса дуги и радиуса сопряжения, до пересечения дополнительной прямой. Точка пересечения является центром сопряжения. Из получившейся точки проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит данную окружность с прямой.

1. Внешнее сопряжение окружностей — сопряжение, при котором центры сопрягаемых дуг находятся вне сопрягающей дуги.

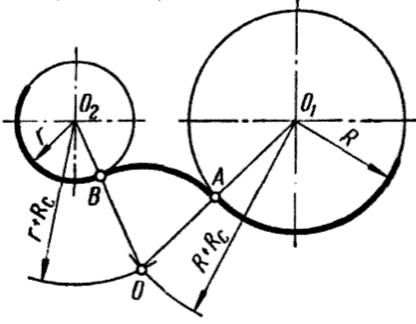Выполняют в следующей последовательности: из центра первой окружности проводят дугу, радиус которой равен сумме радиуса этой окружности и радиуса сопряжения. Аналогично проводим дугу из центра второй окружности. Точка пересечения этих дуг является центром сопряжения. Из получившейся точки проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит обе окружности.

1. Внутреннее сопряжение окружностей — сопряжение, при котором центры сопрягаемых дуг находятся внутри сопрягающей дуг.

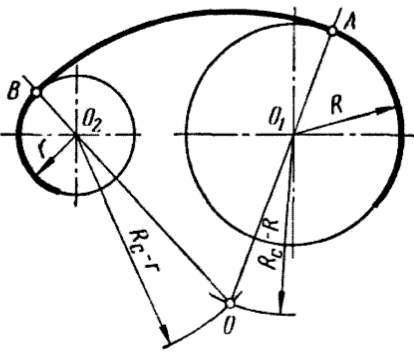Выполняют в следующей последовательности: из центра первой окружности проводят дугу, радиус которой равен разности радиуса сопряжения и радиуса этой окружности. Аналогично проводим дугу из центра второй окружности. Точка пересечения этих дуг является центром сопряжения. Из получившейся точки проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит обе окружности.

1. Смешанное сопряжение окружностей — сопряжение, при котором центр одной из сопрягаемых окружностей лежит внутри сопрягающей дуги, а центр другой сопрягаемой окружности вне нее.

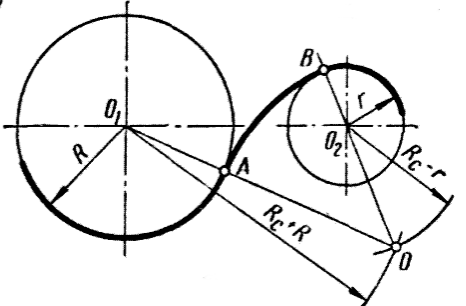Выполняют в следующей последовательности: из центра первой окружности проводят дугу, радиус которой равен сумме радиуса этой окружности и радиуса сопряжения. Из центра второй окружности проводят дугу, радиус которой равен разности радиуса сопряжения и радиуса этой окружности. Точка пересечения этих дуг является центром сопряжения. Из получившейся точки проводят дугу, радиус которой равен радиусу сопряжения. Эта дуга плавно соединит обе окружности.

Примеров использования сопряжения линий в машиностроении существует великое множество — от мелких элементов деталей до достаточно крупных.

Например:

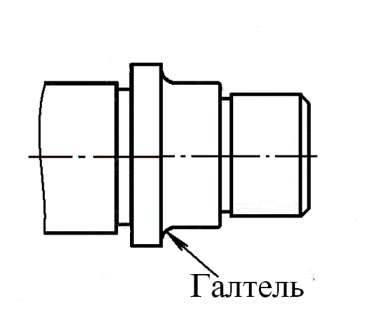— галтель — плавный переход от одного диаметра вала к другому.

— шпоночный паз (а) и шпонка (б), лопасть (в), некоторые поверхности инструментов (г) и т. д.

а) б)

в) г)

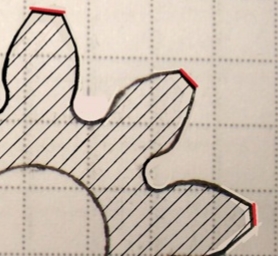
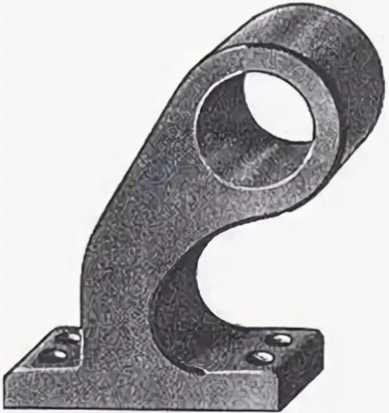
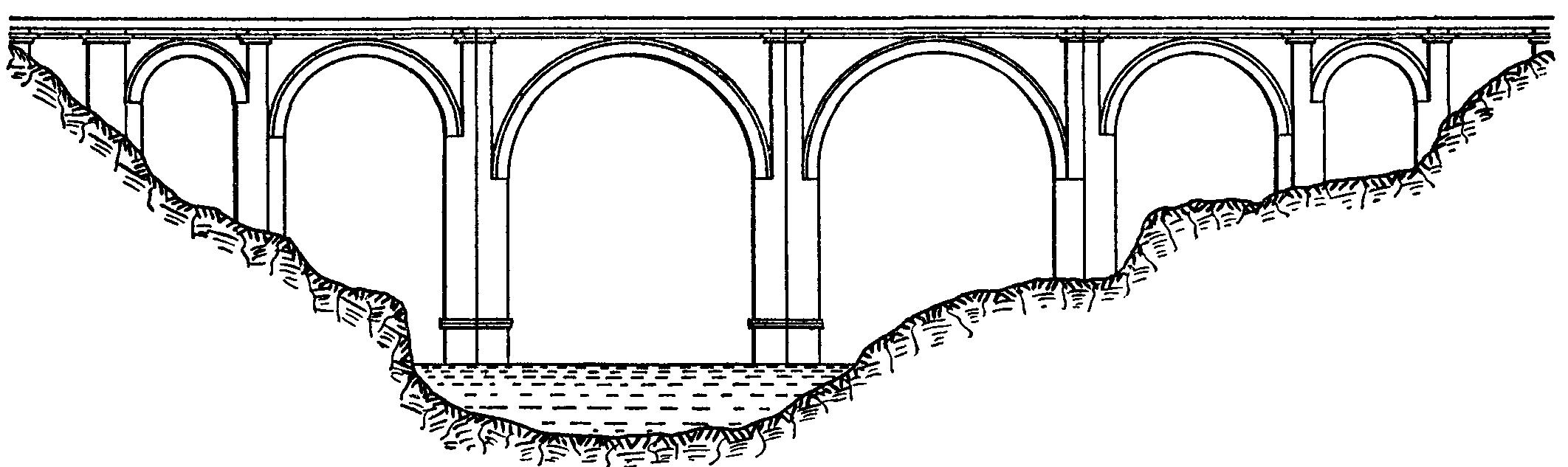Сопряжение линий издавна активно применялось при проектировании различных строений. Самыми яркими примерами являются декоративные арки, пролеты мостов.

Сопряжения линий является очень распространенным окружающем нас мире, что всех примеров применений не перечислить, но все они делаются с одной целью — скругление острых углов для обеспечения безопасности.

Сопряжение линий в искусстве прослеживается на картинах, а также в форме различных изделий (например — ваз).

С опряжение линий в природе встречается в различных формах, например: плавный склон горы, муравейник, пчелиные соты, древесный лист или даже в виде дерева.

П о предыдущим примерам определите наиболее подходящие виды сопряжения: