Цели урока:
- повторение и обобщение изученного материала;
- корректирование знаний учащихся;
- формирование умений рассуждать, применять полученные знания.
Ход урока
Устная работа по готовому чертежу
Мы знакомы с теоремами и их следствиями, которые устанавливают взаимосвязь между углами и сторонами в треугольнике. Используя эти теоремы, а также данные чертежа, придумайте всевозможные задачи.
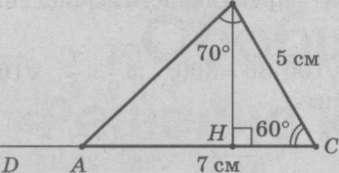
Учащиеся, используя данные чертежа (рис. 1), могут предложить следующие задачи.
Найти величину угла А в треугольнике АВС.
Найти внешний угол DAB треугольника АВС.
Найти градусные меры углов АВН и СВН.
Сравнить длины сторон треугольников АВН и ВНС.
Выяснить, является ли отрезок ВН биссектрисой треугольника АВС.
Очень важно, чтобы, формулируя задачу и отвечая на вопрос, поставленный в ней, учащийся ссылался на теорему или следствия и правильно озвучивал их.
После рассмотрения задач, предложенных учащимся, целесообразно еще раз вернуться к формулировкам известных теорем и свойств треугольника. Опрос может проходить как в устной форме, так и в форме математического диктанта. Его содержание может быть таким.
Закончите предложения (1-10).
В треугольнике сумма углов равна…
Внешний угол треугольника равен…
Если один из внешних углов треугольника равен 90 градусов, то…
В треугольнике против большей стороны лежит…
В треугольнике против меньшего угла лежит…
Если в треугольнике два угла равны, то…
Сумма двух сторон треугольника…
Длина гипотенузы в прямоугольном треугольнике…
Во всяком треугольнике против равных сторон лежат…
Катет, лежащий против угла в 30 градусов, равен…
При оценивании результатов диктанта можно использовать следующие критерии отметки:
«3» - 5-6 верных ответов;
«4» - 7-8 верных ответов;
«5» - 9-10 верных ответов.
Решение задач
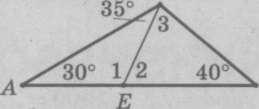
Найдите углы 1-3 в треугольнике АВС, используя данные рисунка 2.
Ответ. <1 = 115 градусов, <2 = 65 градусов, <3 = 75 градусов.
В равнобедренном треугольнике угол при основании в два раза больше угла, противолежащего основанию, Найдите углы этого треугольника.
Ответ: 36 градусов, 72 градуса, 72 градуса.
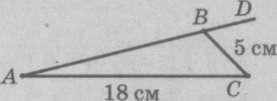
На продолжении стороны АВ треугольника АВС за вершину В отмечена точка D, АС = 18 см, В = 5 см (рис. 3). Может ли отрезок AD быть равным 12 см?
Решение. Из неравенства треугольника следует, что АВ > 13 cм (АВ + ВС > AC). Так как отрезок АD > AB, то длина отрезка AD не может равняться 12 см.
Итог урока
На сегодняшнем уроке мы обобщили знания о взаимосвязи между элементами в треугольнике, повторили необходимые теоремы, следствия, разобрали основные приемы решения задач по теме, оценили свой уровень знаний.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Соотношения и расстояния между сторонами и углами треугольника (31.05 КB)
Соотношения и расстояния между сторонами и углами треугольника (31.05 КB)
 1
1 570
570 44
44 Нравится
0
Нравится
0


