Смежные углы

Презентация содержит материалы к двум урокам геометрии.

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными

Угол ACB и угол BCD – смежные

CB - сторона общая

CA и CD - являются продолжениями одна другой.

ТЕОРЕМА 2.1

Сумма смежных углов равна 180°

В презентации представлено доказательство данной теоремы.

Устная работа:

Один из смежных углов 30°  Найди другой угол.

Один из смежных углов 112° Найди другой угол.

Задача.

Найдите смежные углы, если градусная мера одного из них на 40% больше градусной мера другого.

Всего презентация содержит 28 слайдов.

СМЕЖНЫЕ УГЛЫ

• Определение,
• Свойства
• Учитель Козина Н.А.

СМЕЖНЫЕ УГЛЫ

• Определение

Учебник. Стр. 22.

• Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными

СМЕЖНЫЕ УГЛЫ

• Определение

Учебник. Стр. 22.

•  ACB и  BCD – смежные

• CB - сторона общая
• CA и CD - являются продолжениями одна другой.

B

A

D

C

СМЕЖНЫЕ УГЛЫ

• Найдите и запишите пары смежных углов на рисунке.

P

F

Q

N

M

СМЕЖНЫЕ УГЛЫ

• Найдите и запишите пары смежных углов на рисунке.

B

C

A

D

O

•  AOB и  BOD;
•  AOC и  COD.

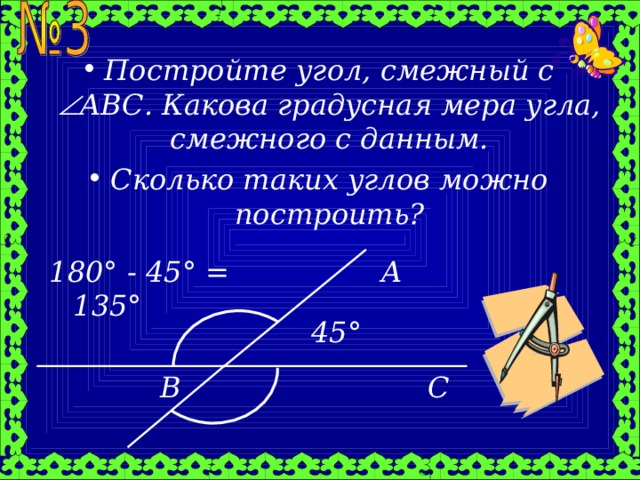
• Постройте угол, смежный с  ABC . Какова градусная мера угла, смежного с данным.
• Сколько таких углов можно построить?

180 ° - 45 ° = 135 °

A

45 °

B

С

ТЕОРЕМА 2.1

• Сумма смежных углов равна 180 °

• Дано:  AOC и  COB – смежные ;
• Доказать:

•  AOC +  COB = 180°.

C

O

A

B

• Доказательство.

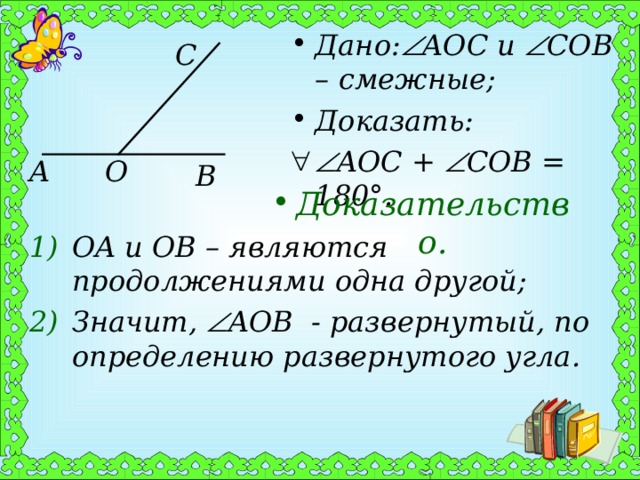
• Дано:  AOC и  COB – смежные ;
• Доказать:

•  AOC +  COB = 180°.

C

A

O

B

• Доказательство.

• OA и OB – являются продолжениями одна другой;
• Значит,  AOB - развернутый, по определению развернутого угла.

C

• Доказательство.

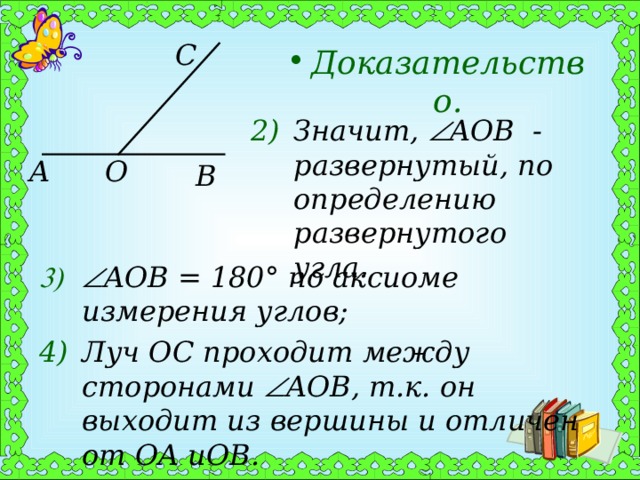
• Значит,  AOB - развернутый, по определению развернутого угла.

A

O

B

•  AOB = 180° по аксиоме измерения углов;

• Луч OC проходит между сторонами  AOB , т.к. он выходит из вершины и отличен от OA и OB .

C

• Доказательство.

• Луч OC проходит между сторонами  AOB , т.к. он выходит из вершины и отличен от OA и OB .

A

O

B

• Значит, по аксиоме измерения углов, имеем  AOC +  COB =  AOB = 180°
• Теорема доказана.

• Один из смежных углов 30 °
• Найди другой угол.
• 150 ° .

C

O

A

B

• Один из смежных углов 112 °
• Найди другой угол.
• 68 ° .

C

N

• Найдите градусные меры

•  KLN и  LPN

70°

K

25°

P

L

M

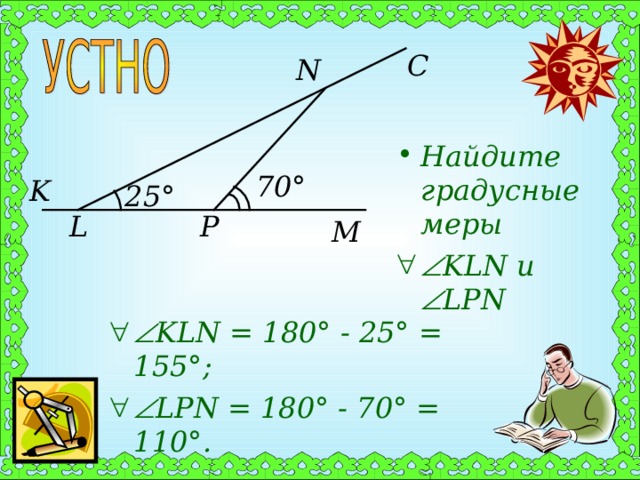
•  KLN = 180° - 25° = 155°;
•  LPN = 180° - 70° = 110°.

C

ЗАДАЧА №5

• Найдите смежные углы, если градусная мера одного из них на 40% больше градусной мера другого.

O

A

B

• Дано:  AOC и  COB – смежные ;

•  AOC на 40% больше
•  COB

1,4x°

x°

180°

• Ответ:  AOC = 105°,  COB = 75°.

ДОМАШНЕЕ ЗАДАНИЕ

• Учебник.П14. Вопросы 1 – 5. Стр. 30.
• Задачи №3, №4(1). Стр. 30.
• Принести транспортир.
• Рабочая тетрадь
• № 77, 78, 79(выучить устно),
• 82, 83, 84.

СМЕЖНЫЕ УГЛЫ

Следствия.

Решение

задач.

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Начертите угол AOB .
• Начертите угол с ним смежный.
• Обозначьте его.
• Измерьте эти углы.
• Сделайте записи.

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Один из смежных углов равен 123 ° . Найдите второй угол.

• Острым, тупым или прямым будет угол, смежный с углом в 30 ° .

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• Являются ли смежными углы AOC и COB ?

С

A

B

O

• Найдите смежные углы, если один из них на 30 ° больше другого (без оформления).

СМЕЖНЫЕ УГЛЫ

Следствия.

Следствием из данной теоремы называют такое утверждение, которое доказывается со ссылкой только на данную теорему.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Если два угла равны, то смежные с ними углы равны.
• Если угол не развернутый, то его градусная мера меньше 180 ° .
• Угол, смежный с прямым углом, есть прямой угол.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Если два угла равны, то смежные с ними углы равны.

• Доказательство в рабочей тетради стр. 17.

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Если угол не развернутый, то его градусная мера меньше 180 ° .

С

Дано:  CAF – не

развернутый.

Доказать:  CAF

A

F

0;  CAF 0, значит,  CAF " width="640"

С

Дано:  CAF – не

развернутый.

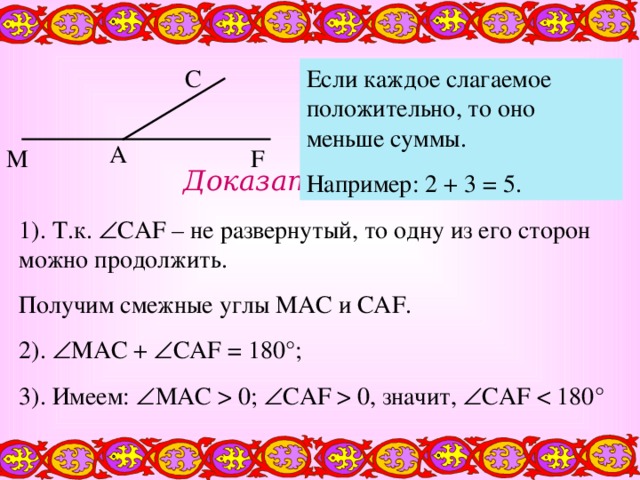
Если каждое слагаемое положительно, то оно меньше суммы.

Например: 2 + 3 = 5.

Доказать:  CAF

A

F

M

Доказательство.

1). Т.к.  CAF – не развернутый, то одну из его сторон можно продолжить.

Получим смежные углы MAC и CAF .

2).  MAC +  CAF = 180 °;

3). Имеем:  MAC 0;  CAF 0, значит,  CAF

СМЕЖНЫЕ УГЛЫ

Следствия.

Учебник. Стр.25.

• Угол, смежный с прямым углом, есть прямой угол.

F

Дано:  F BD = 90 ° ,  F BD и  KBF – смежные.

K

B

D

Доказать:  KBF = 90 ° .

Устно, самостоятельно.

ЗАДАЧА №1

Найдите смежные углы, если одна третья часть одного из них равна 0,2 другого.

Дано:  AOC и  COB – смежные.

C

B

A

O

Найти:  AOC и  COB.

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

Дано:  AOC и  COB – смежные.

C

B

A

O

Найти:  AOC и  COB.

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

Решение.

•  AOC +  COB = 180 ° по свойству смежных углов.

• Пусть  AOC = x °, тогда  COB = (180 – x) °;

• 180 ° - 67,5° = 112,5°;

Ответ:  AOC = 67,5 °;

 COB = 112,5 ° .

ДОМАШНЕЕ ЗАДАНИЕ

• Учебник.
• Вопросы 1 – 5.
• Задачи:
• № 4(2), №6(1).
• Рабочая тетрадь
• № 88, №89.