Цель урока:
познакомить учащихся с понятиями смежных углов, вертикальных углов, односторонних углов, накрест лежащих углов; рассмотреть их свойства.
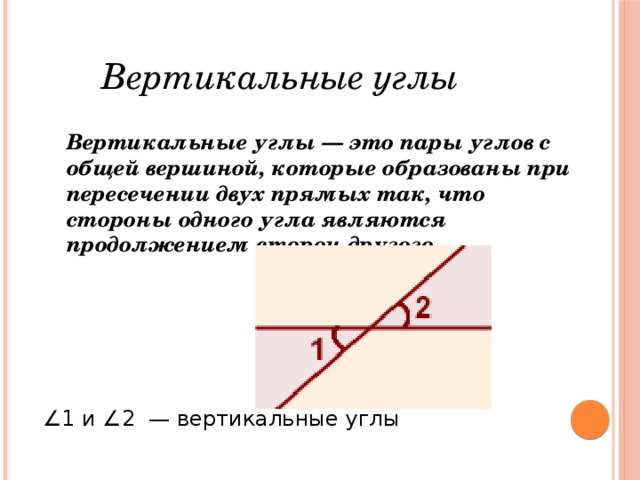
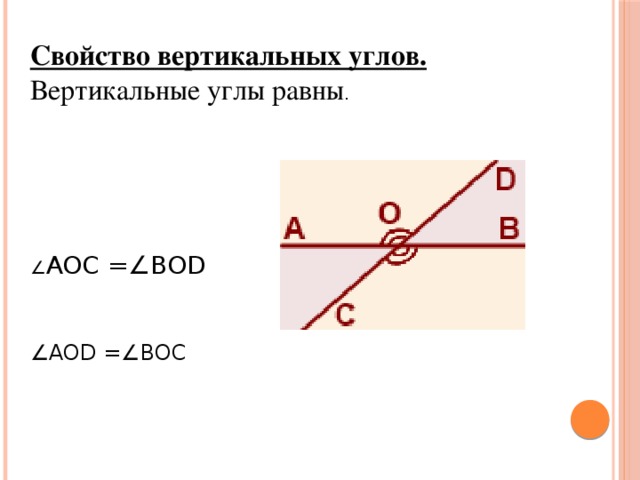
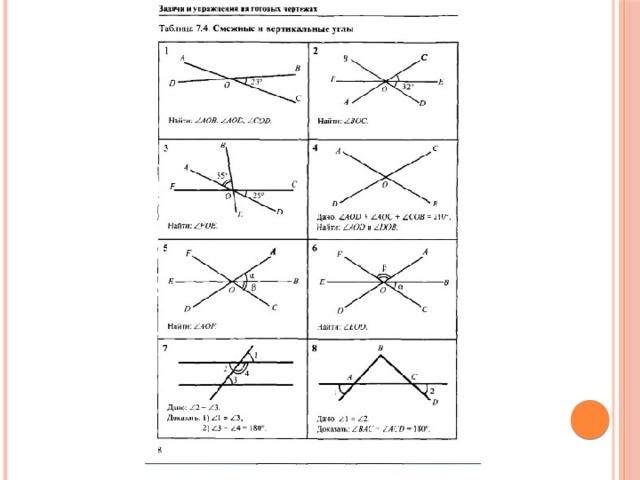
Углы: смежные, вертикальные, односторонние, накрест лежащие.
Смежные углы
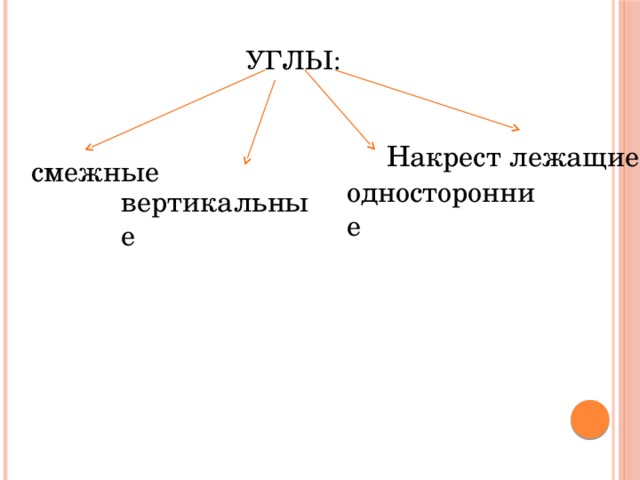
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.
- Сколько смежных углов образуется при пересечении двух прямых?
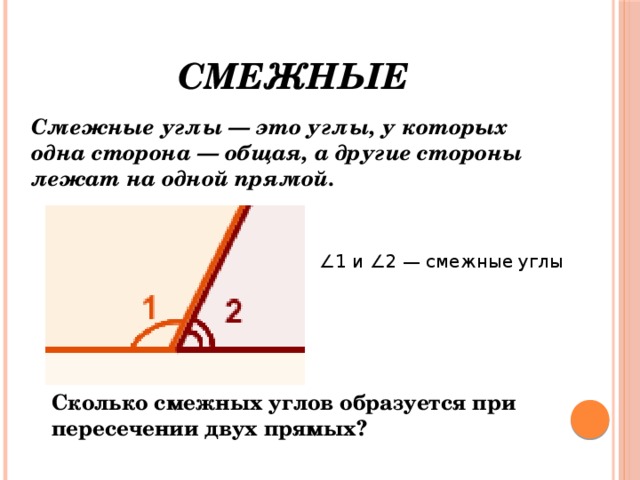
При пересечении двух прямых образуется четыре пары смежных углов.
Свойство смежных углов.
Сумма смежных углов равна 180º.
Задача:
Угол 1 равен 38 градусов, сколько градусов равен смежный с ним угол?

Односторонние углы
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми, — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
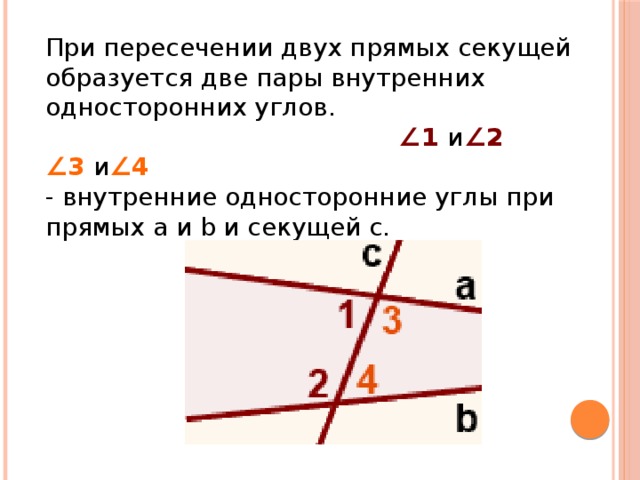
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.
Свойства внутренних односторонних углов, образованных параллельными прямыми и секущей:
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.
Если a ∥ b, то ∠1 +∠2 =180º (как внутренние односторонние при a ∥ b и секущей c).
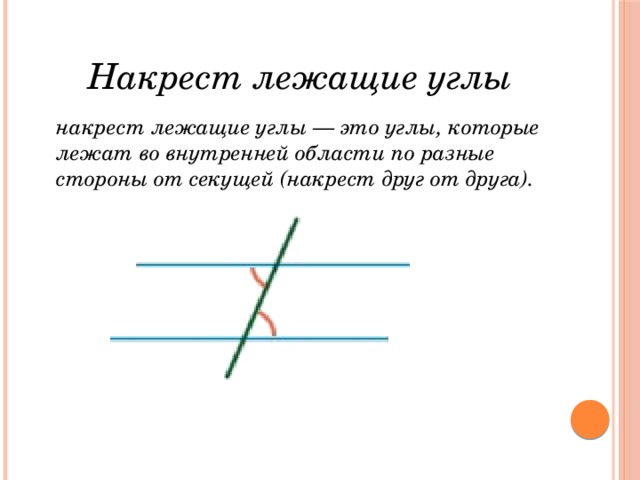
Накрест лежащие углы
Накрест лежащие углы — это углы, которые лежат во внутренней области по разные стороны от секущей (накрест друг от друга).
Свойства накрест лежащих углов: накрест лежащие углы равны.
Задача:
Назвать все углы на рисунке.

 Получите свидетельство
Получите свидетельство Вход
Вход





















 Презентация по математике по теме "Углы" (0.18 MB)
Презентация по математике по теме "Углы" (0.18 MB)
 0
0 6722
6722 145
145 Нравится
0
Нравится
0