Цель:
ввести понятия смежных и вертикальных углов; сформировать умение решать задачи с использованием этих углов.
Задачи:
Подвести обучающихся к понятию смежных и вертикальных углов;
Дать определение смежных и вертикальных углов и их свойств;
Создать ситуацию, которая позволит учащимся самостоятельно сформулировать понятие вертикальных и смежных углов и их свойств;
Сформировать умение решать задачи с использованием этих углов.
Предметные результаты:
Знать:
Определения понятий «смежный угол», «вертикальный угол»;
Свойство смежных углов;
Свойство вертикальных углов.
Уметь:
Определять вертикальные и смежные углы по определению;
Различать смежные и вертикальные углы;
Применять свойства смежных и вертикальных углов при решении задач.
План-конспект урока.
Обучение ведется по учебнику Г.В.Дорофеева, И.Ф.Шарыгина «Математика 6». Соответствующая программа предполагает, что обучающиеся познакомились с понятием прямая, угол, виды углов в 5 классе.
1. Организационный момент.
2. Устная работа.
Восстановите цепочку вычислений.
(Обучающие выполняют устный счет)
3. Актуализация знаний.
Учитель. Ребята, посмотрите внимательно видеофрагмент [1]
Учитель. Вы посмотрели видеофрагмент. Ответьте на следующие вопросы:
Конечна или бесконечна прямая?

Сколько прямых можно провести через две точки?
Что такое луч?
Что такое угол?
Что такое вершина угла? стороны угла?
В чем измеряются углы?
Скольким градусам равен развернутый угол?
(Обучающиеся смотрят видеофрагмент и отвечают на поставленные вопросы)
Работы в парах.
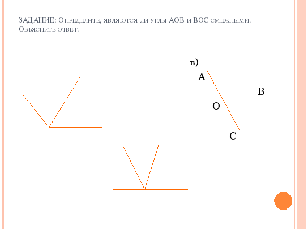
Учитель. Посмотрите внимательно на углы, разделите все углы на группы.
На сколько групп можно разделить изображенные углы?(2 группы)
Как можно назвать образованные группы? (углы и углы образованные при пересечении прямых)
Как вы думаете о чем сегодня пойдет речь на уроке?
На уроке мы познакомимся с углами образованными при пересечении прямых и их свойствами.
Открываем рабочие тетради, записываем число, классная работа.
4. Объяснение нового материала.
Учитель. Пусть у нас имеется развернутый угол АОВ. Из точки О проведем луч ОС. Какие при этом углы получились? (углы АОС и ВОС)
Углы АОС и ВОС называются смежными.
(Обучающиеся вместе с учителем строят углы и затем записывают определение смежных углов)
Слайд 1.(Работа в группах)
Задание. Определите, являются ли углы АОВ и ВОС смежными (а,в – нет, б - да)
Учитель. Попробуйте сформулировать, какие два угла называются смежными.
Целесообразно спросить нескольких обучающихся, при необходимости поправляя их.
Учитель. Заполним пропуски нужными словами, и мы получим определение смежных углов.
Два угла называются смежными, если у них одна сторона общая, а две другие составляют прямую линию.
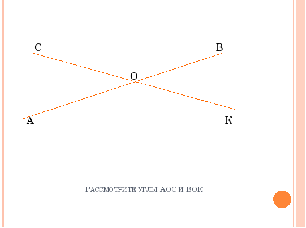
Учитель. Вернемся к чертежу [2]. Будем перемещать луч ОА и посмотрим как изменятся величины смежных углов.
Известна величина одного из смежных углов. Можно найти величину другого угла? (можно)
Чему она равна?
Таким образом, давайте сформулируем свойство смежных углов.
Свойство. Сумма смежных углов равна 180º
(Обучающиеся записывают свойство смежных углов в тетрадь)
Слайд 2.
Учитель. Пусть у нас есть две прямые АВ и СК, которые пересекаются в точке О.
Рассмотрим углы АОС и ВОК. Какую особенность имеют стороны этих углов? (сторона АО и ВО лежат на одной прямой)
Теперь рассмотрим углы АОК и ВОС. Что можно сказать о них? (стороны СО и СК лежат на одной прямой)
Такие пары углов называются вертикальными.
Слайд 3.(Работа в группах)
Задание. Определите, являются ли углы АОС и ВОК вертикальными (а,б – нет, в – да)
Учитель. Попробуйте сформулировать, какие два угла называются вертикальными.
Целесообразно спросить нескольких обучающихся, при необходимости поправляя их.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход




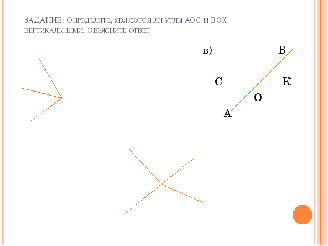









 Конспект урока по математике «Пересекающиеся прямые» (0.27 MB)
Конспект урока по математике «Пересекающиеся прямые» (0.27 MB)
 0
0 5718
5718 1290
1290 Нравится
0
Нравится
0


