Сложение вероятностей

УРОК 1.4 « Сложение и умножение вероятностей »

Цели: рассмотреть примеры вероятностей на сложение и умножение.

Ход урока

I. Объяснение нового материала

1. Задача 1. В ящике лежат 50 шаров. 18 синих шаров, 12 красных и 20 желтых. Наугад вынимают 1 шар. Найти вероятность, что шар оказался не желтым?

а) Событие А – шар оказался синим: Р(А) =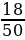

б) Событие В – шар оказался красным: Р(В) =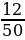

События А и В одновременно произойти не могут. Говорят, что события А и В – несовместные.

Два события называются несовместными, если наступление одного из них исключает наступление другого.

Тогда вероятность, что шар оказался не желтым будет равна Р(С) = Р(А) + Р(В), т.е.

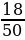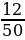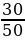+ = = 0,6

Если наступает только одно из двух несовместных событий, то вероятности складываются.

1) На эк­за­ме­не по гео­мет­рии школь­ни­ку достаётся одна за­да­ча из сбор­ни­ка. Ве­ро­ят­ность того, что эта за­да­ча по теме «Углы», равна 0,1. Ве­ро­ят­ность того, что это ока­жет­ся за­да­ча по теме «Па­рал­ле­ло­грамм», равна 0,6. В сбор­ни­ке нет задач, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся за­да­ча по одной из этих двух тем.

2) На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Площадь», равна 0,15. Вероятность того, что это окажется задача по теме «Окружность», равна 0,3. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.

Задача 2. В одном из двух ящиков находятся 10 шаров, из которых 7 красных и 3 желтых, а в другом - 15 шаров, из которых 5 красных и 10 желтых. Из каждого ящика наугад вынимают по одному шару. Найти вероятность того, что оба шара окажутся желтыми.

а) Событие А – из первого ящика вынимают желтый шар: Р(А) =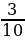

б) Событие В – из второго ящика вынимают желтый шар: Р(В) =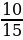

События А и В являются независимыми, т.е. вытаскивание желтого шара из первого ящика никак не влияет на вытаскивание желтого шара из второго ящика.

Два события называются независимыми, если наступление одного из них не зависит от наступление другого.

Тогда вероятность, что оба шара окажутся желтым будет равна Р(С) = Р(А) 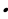Р(В), т.е.

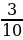
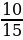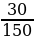= = 0,2

Если наступают два независимых события, то вероятности умножаются.

№ 824

Задача 3. Вероятность попадания в мишень одного стрелка равна 0,9, а другого – 0,8. Каждый сделал по одному выстрелу. Какова вероятность, что мишень будет поражена?

а) Событие А – первый стрелок попал в мишень

б) Событие В – второй стрелок попал в мишень

в) мишень поражена

События А и В являются независимыми. Но воспользоваться умножением вероятностей в этом случае нельзя, т.к. мишень будет поражена и при попадании в цель только одного стрелка. В этом случае считаем иначе. Находим противоположные события.

Вероятность, что промахнулся первый стрелок: Р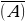 = 1 – 0,9 = 0,1;

промахнулся второй стрелок: Р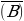 = 1 – 0,8 = 0,2.

События А и В являются независимые, значит вероятность промаха обоих стрелков

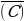Р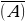 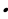= Р Р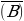 , т.е. 0,1 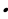0,2 = 0,02, следовательно, вероятность, что мишень будет

поражена Р(С) = 1 – 0,02 = 0,98

№ 828.

II. Формирование умений и навыков.

,

II. Формирование умений и навыков.

III

IV. . Формирование умений и навыков.

V. Домашнее задание:

П. №№