Муниципальное бюджетное образовательное учреждение
Средняя общеобразовательная школа № 33 имени
Героя Советского Союза Л.П. Тихмянова
УТВЕРЖДАЮ
Директор МБОУ - СОШ № 33
_____________ Н.Н. Акулова
приказ _______от ______2013 года
РАБОЧАЯ ПРОГРАММА
по алгебре
в 9 « Б » классе
2013 – 2014 учебный год
Составитель программы:
учитель математики
Панина Елена Юрьевна
Программа рассмотрена на заседании школьного методического объединения
Протокол № __ от «__»_________2013г.
Руководитель__________________________( _______ __________)
1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
1.1 Нормативно-правовая база.
Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 9 классов и реализуется на основе следующих документов:
1.Закон РФ «Об образовании», п.7,ст.32;
2. Письмо Департамента образования от 13.11.2002 г. «»О развитии содержания
общего образования.
3.Программа для общеобразовательных школ, гимназий, лицеев:
Сборник “Программы для общеобразовательных школ, гимназий, лицеев:
Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.-
М. Дрофа, 2002; 4-е изд. – 2004г.
4.Стандарт основного общего образования по математике.
Стандарт основного общего образования по математике //Математика в школе. –
2004г,-№4, -с.4
5.Федерального перечня учебников, рекомендованных Министерством образования
Российской Федерации к использованию в образовательном процессе в
общеобразовательных учреждениях на 2012-2013 учебный год,
Данная рабочая программа соответствует учебнику «Алгебра 9» автор Макарычев Ю.Н. и др. (изд.Москва «Просвещение, 2009).
1.2 Место предмета в федеральном базисном учебном плане.
В соответствии с учебным планом МБОУ-СОШ №33 на изучение алгебры в 9 классе отводится 3 часа в неделю, 102 часа согласно Федеральному базисному учебному плану для образовательных учреждений Российской .
1.3 Причины создания рабочей программы.
В настоящей рабочей программе изменено соотношение часов на изучение тем, в связи с их сложностью. Для более широкого знакомства с математикой введен курс «Элементы комбинаторики и теории вероятностей» количестве 9 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.
1.4 Общая характеристика учебного предмета.
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально- графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В курсе алгебры 9 класса расширяются сведения о свойствах функций, познакомить обучающихся со свойствами и графиком квадратичной функции; систематизируются и обобщаются сведения о решении целых и дробных рациональных уравнений с одной переменной, формируется умение решать неравенства вида ах2 + bх + с0 ах2 + bх + с
.
1.5 Цели обучения.
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся овладевают приёмами вычислений на калькуляторе
1.6 Структура рабочей программы.
Рабочая программа включает следующие разделы:
пояснительную записку;
основное содержание;
примерное распределение учебных часов по разделам программы;
требования к уровню подготовки учащихся данного класса;
тематическое планирование учебного материала;
поурочное планирование;
примерные контрольные работы;
учебное и учебно-методическое обеспечение обучения.
1.7 Обоснование увеличения/ уменьшения часов.
1.8 Формы и методы обучения.
Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий: игровое моделирование (дидактические игры, работа в малых группах, работа в парах сменного состава); проблемное обучение; личностно ориентированное обучение.
Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений.
Учебный процесс ориентирован на:
создание оптимальных условий обучения;
исключение психотравмирующих факторов;
сохранение психосоматического состояния здоровья учащихся;
развитие положительной мотивации к освоению программы;
развитие индивидуальности и одаренности каждого ребенка.
рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач;
сбалансированное сочетание традиционных и новых методов обучения;
оптимизированное применение объяснительно-иллюстративных и эвристических методов;
использование современных технических средств обучения.
2.ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ.
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
АРИФМЕТИКА
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
АЛГЕБРА
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к 0, у=кх+b, у=х2, у=х3, у = , у= , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики; хк х
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
3.УЧЕБНО - ТЕМАТИЧЕСКИЙ ПЛАН.
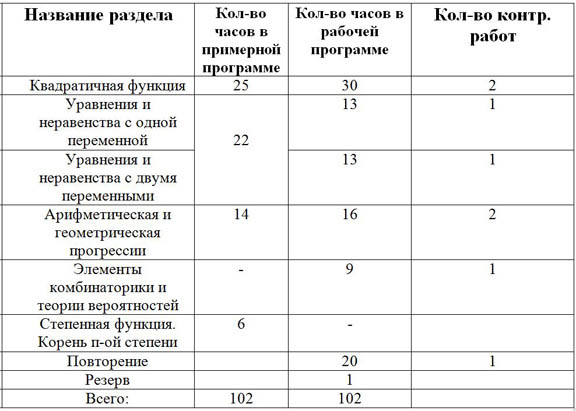
| № п/п | Название раздела | Кол-во часов в примерной программе | Кол-во часов в рабочей программе | Кол-во контр. работ |
-
| Квадратичная функция | 25 | 30 | 2 |
-
| Уравнения и неравенства с одной переменной |
22 | 13 | 1 |
-
| Уравнения и неравенства с двумя переменными | 13 | 1 |
-
| Арифметическая и геометрическая прогрессии | 14 | 16 | 2 |
-
| Элементы комбинаторики и теории вероятностей | - | 9 | 1 |
-
| Степенная функция. Корень п-ой степени | 6 | - |
|
-
| Повторение |
| 20 | 1 |
-
| Резерв |
| 1 |
|
|
| Всего: | 102 | 102 |
|
4. СОДЕРЖАНИЕ ПРОГРАММЫ УЧЕБНОГО КУРСА.
Содержание тем учебного курса
1. Квадратичная функция
Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = а х 2 +вх + с, ее свойства и график. Простейшие преобразования графиков функций. Функция у = х n и ее свойства. Корень n – степени и его свойства. Свойства степени с рациональным показателем.
Основная цель: выработать умение строить график квадратичной функции.
Обучающиеся должны знать: определение функции; понятие возрастания и убывания функции; определение квадратичной функции; формулу для разложения квадратного трехчлена на множители; определение корня n – степени и его свойства; определение степени с рациональным показателем и ее свойства.
Обучающиеся должны уметь: работать с графиком функции: находить область определения и область значений, промежутки возрастания и убывания; строить график квадратичной функции и работать с ним; раскладывать квадратный трехчлен на множители и применять это разложение для сокращения дробей; преобразовывать выражения, содержащие корень n –степени и выражения, содержащие степень с рациональным показателем.
Контрольные работы-2
2. Уравнения и неравенства с одной переменной
Целое уравнение и его корни. Решение уравнений с помощью новой переменной. Решение неравенств второй степени с одной переменной. Решение неравенств методом интервалов.
Основная цель: выработать навыки в решении целых и дробных уравнений с помощью новой переменной; выработать навыки в решении неравенств второй степени с одной переменной и решении неравенств методом интервалов.
Обучающиеся должны знать: определение целого уравнения и его корней; принцип метода интервалов.
Обучающиеся должны уметь: решать целые и дробные уравнения; решать неравенства второй степени с одной переменной; применять метод интервалов для решения неравенств.
Контрольная работа-1
3. Уравнения и неравенства с двумя переменными
Уравнение с двумя переменными и его график. Графический способ решения систем уравнений. Решение систем уравнений второй степени способом подстановки и способом сложения. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Основная цель: выработать умение решать простейшие системы, содержащие уравнения второй степени, и решать текстовые задачи с помощью составления таких систем.
Обучающиеся должны знать: графики уравнений с двумя переменными.
Обучающиеся должны уметь: решать системы уравнений второй степени различными способами; решать текстовые задачи с помощью таких систем.
Контрольная работа-1
4. Арифметическая и геометрическая прогрессии
Определение арифметической и геометрической прогрессий. Формулы n – члена и суммы n первых членов этих прогрессий.
Основная цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностей особого вида.
Обучающиеся должны знать: определения арифметической и геометрической прогрессий; формулы n – члена, формулы суммы n первых членов прогрессий.
Обучающиеся должны уметь: выполнять задания, связанные с непосредственным применением изучаемых формул; выполнять задачи практического содержания.
Контрольные работы-2
5. Элементы комбинаторики и теории вероятности
Примеры комбинаторных задач. Перестановки. Размещения. Сочетания. Относительная частота случайного события. Вероятность равновозможных событий.
Основная цель: познакомить учащихся с элементами комбинаторики и начальными сведениями из теории вероятности.
Обучающиеся должны знать: понятие перестановки, размещения и сочетания.
Обучающиеся должны уметь: применять эти понятия в процессе решения задач; вычислять вероятность события.
Контрольная работа-1
6. Повторение
Преобразование алгебраических выражений. Решение целых и дробных уравнений. Решение систем уравнений. Решение линейных неравенств. Системы линейных неравенств. Решение неравенств второй степени. Системы неравенств второй степени. Арифметический квадратный корень Степень с рациональным показателем. Арифметическая прогрессия. Геометрическая прогрессия. Функции и их графики. Решение уравнений и систем уравнений графическим способом. Решение текстовых задач на составление уравнений. Решение задач на проценты.
Основная цель: закрепление умений в решении заданий по курсу алгебры 7 – 9 классов.
Итоговая контрольная работа
КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
ПО АЛГЕБРЕ В 9 КЛАССЕ
Класс: 9 « Б »
Годовое количество часов: 102
Количество часов в неделю: 3
Плановое количество контрольных работ:
I ч -
II ч -
III ч -
IV ч –
| № п/п | Содержание материала | Количество часов | Дата |
| Глава 1.Квадратичная функция . | 30 |
|
| § 1. Функции и их свойства | 6 |
|
| 1 | Функция. | 1 |
|
| 2 | Область определения и область значений функции | 1 |
|
| 3 | Нули функции | 1 |
|
| 4 | Возрастание и убывание функции | 1 |
|
| 5 | Возрастание и убывание функции | 1 |
|
| 6 | Изучение свойств функции с помощью графика | 1 |
|
| § 2. Квадратный трехчлен. | 4 |
|
| 7 | Квадратный трехчлен и его корни | 1 |
|
| 8 | Разложение квадратного трехчлена на множители | 1 |
|
| 9 | Применение разложения квадратного трехчлена на множители для сокращения дробей | 1 |
|
| 10 | Решение задач на разложение квадратного трёхчлена на множители | 1 |
|
| § 3. Квадратичная функция и её график. | 7 |
|
| 11 | Функция у = ах 2, ее свойства и график (а 0) и (а | 1 |
|
| 12 | График функции у = ах 2+n | 1 |
|
| 13 | График функции у = а (х – m) 2 | 1 |
|
| 14 | Построение графика квадратичной функции | 1 |
|
| 15 | Свойства и график квадратичной функции | 1 |
|
| 16 | Повторение темы «Квадратичная функция» | 1 |
|
| 17 | Контрольная работа № 1 по теме «Квадратичная функция» | 1 |
|
| § 4. Степенная функция. Корень п –ой степени. | 13 |
|
| 18 | Анализ к.р. № 1. Четные и нечетные функции | 1 |
|
| 19 | Функция у = х n | 1 |
|
| 20 | Свойства функции у = х n | 1 |
|
| 21 | Определение корня n – степени | 1 |
|
| 22 | Нахождение значений выражений, содержащих корень n – степени | 1 |
|
| 23 | Преобразование выражений, содержащих корень n – степени | 1 |
|
| 24 | Решение задач на вычисление корня n – степени | 1 |
|
| 25 | Определение степени с рациональным показателем | 1 |
|
| 26 | Свойства степени с рациональным показателем | 1 |
|
| 27 | Применение свойств степени для упрощения выражений | 1 |
|
| 28 | Преобразование дробей, содержащих степень с рациональным показателем | 1 |
|
| 29 | Повторение темы: «Корень n – степени» и «Степень с рациональным показателем» | 1 |
|
| 30 | Контрольная работа № 2 по теме «Степенная функция и корень n – степени » | 1 |
|
| Глава 2. | Уравнения и неравенства с одной переменной. | 13 |
|
| § 5. Уравнения с одной переменной. | 5 |
|
| 31 | Целое уравнение и его корни. Решение целых уравнений | 1 |
|
| 32 | Решение уравнений с помощью новой переменной | 1 |
|
| 33 | Решение биквадратных уравнений | 1 |
|
| 34 | Дробные рациональные уравнения | 1 |
|
| 35 | Решение дробных рациональных уравнений с помощью новой переменной | 1 |
|
| § 6. Неравенства с одной переменной. | 8 |
|
| 36 | Решение неравенств второй степени с одной переменной | 1 |
|
| 37 | Нахождение области определения функции с помощью решения неравенств | 1 |
|
| 38 | Доказательство верности неравенств | 1 |
|
| 39 | Метод интервалов | 1 |
|
| 40 | Решение неравенств методом интервалов | 1 |
|
| 41 | Решение задач с помощью метода интервалов | 1 |
|
| 42 | Повторение темы «Целые уравнения и неравенства второй степени» | 1 |
|
| 43 | Контрольная работа № 3 по теме «Целые уравнения и неравенства второй степени» | 1 |
|
| Глава 3. | Уравнения и неравенства с двумя переменными. | 13 |
|
| § 7. Уравнения с двумя переменными и их системы. | 10 |
|
| 44 | Анализ к.р. № 3. Уравнение с двумя переменными и его график | 1 |
|
| 45 | Уравнение с двумя переменными и его график | 1 |
|
| 46 | Графический способ решения систем уравнений | 1 |
|
| 47 | Решение систем уравнений способом подстановки | 1 |
|
| 48 | Решение систем уравнений способом сложения | 1 |
|
| 49 | Решение систем уравнений второй степени | 1 |
|
| 50 | Решение задач с помощью систем уравнений второй степени | 1 |
|
| 51 | Решение задач с геометрическим содержанием | 1 |
|
| 52 | Решение задач на движение | 1 |
|
| 53 | Решение задач на понятие объема работы | 1 |
|
| § 8. Неравенства с думя переменными и их системы. | 3 |
|
| 54 | Системы неравенств с двумя переменными. | 1 |
|
| 55 | Решение систем неравенств с двумя переменными
| 1 |
|
| 56 | Контрольная работа № 4 по теме «Системы уравнений второй степени» | 1 |
|
| Глава 4. | Арифметическая и геометрическая прогрессии. | 16 |
|
| § 9. Арифметическая прогрессия. | 8 |
|
| 57 | Анализ к.р. № 4. Последовательности | 1 |
|
| 58 | Определение арифметической прогрессии | 1 |
|
| 59 | Формула n – го члена арифметической прогрессии | 1 |
|
| 60 | Решение задач по формуле n – го члена арифметической прогрессии | 1 |
|
| 61 | Формула суммы первых n членов арифметической прогрессии | 1 |
|
| 62 | Решение задач по формуле суммы первых n членов арифметической прогрессии | 1 |
|
| 63 | Решение задач на применение понятия арифметической прогрессии | 1 |
|
| 64 | Контрольная работа № 5 по теме «Арифметическая прогрессия» | 1 |
|
| § 10. Геометрическая прогрессия. | 8 |
|
| 65 | Анализ к.р. № 5. Определение геометрической прогрессии | 1 |
|
| 66 | Формула n – го члена геометрической прогрессии | 1 |
|
| 67 | Решение задач по формуле n – го члена геометрической прогрессии | 1 |
|
| 68 | Формула суммы первых n членов геометрической прогрессии | 1 |
|
| 69 | Решение задач по формуле суммы первых n членов геометрической прогрессии | 1 |
|
| 70 | Формула суммы n членов бесконечно убывающей геометрической прогрессии. | 1 |
|
| 71 | Повторение темы «Геометрическая прогрессия» | 1 |
|
| 72 | Контрольная работа № 6 по теме «Геометрическая прогрессия» | 1 |
|
| Глава 5. | Элементы комбинаторики и теории вероятности . | 9 |
|
| § 11. Элементы комбинаторики. | 5 |
|
| 73 | Анализ к.р. № 7. Комбинаторные задачи | 1 |
|
| 74 | Решение комбинаторных задач. | 1 |
|
| 75 | Перестановки | 1 |
|
| 76 | Размещения. | 1 |
|
| 77 | Сочетания. | 1 |
|
| § 12. Начальные сведения из теории вероятностей. | 4 |
|
| 78 | Вероятность случайного события | 1 |
|
| 79 | Решение задач на вероятность случайного события. | 1 |
|
| 80 | Повторение темы: Элементы комбинаторики. | 1 |
|
| 81 | Контрольная работа №7 по теме «Элементы комбинаторики и теории вероятности» | 1 |
|
| Повторение . | 20 |
|
| 82 | Анализ к/р №7. Повторение. Преобразование алгебраических выражений | 1 |
|
| 83 | Повторение. Решение целых уравнений | 1 |
|
| 84 | Повторение. Решение дробных уравнений | 1 |
|
| 85 | Повторение. Решение систем уравнений | 1 |
|
| 86 | Повторение. Решение линейных неравенств | 1 |
|
| 87 | Повторение. Решение неравенств второй степени | 1 |
|
| 88 | Повторение. Системы линейных неравенств | 1 |
|
| 89 | Повторение. Системы неравенств второй степени | 1 |
|
| 90 | Повторение. Арифметический квадратный корень | 1 |
|
| 91 | Повторение. Степень с рациональным показателем | 1 |
|
| 92 | Повторение. Арифметическая прогрессия | 1 |
|
| 93 | Повторение. Геометрическая прогрессия | 1 |
|
| 94 | Повторение. Функции и их графики | 1 |
|
| 95 | Повторение. Функции и их графики | 1 |
|
| 96 | Повторение. Решение задач на проценты | 1 |
|
| 97 | Повторение. Решение уравнений и систем уравнений графическим способом | 1 |
|
| 98 | Повторение. Решение текстовых задач на составление уравнений | 1 |
|
| 99-100 | Итоговая контрольная работа | 2 |
|
| 101 | Анализ итоговой контрольной работы | 1 |
|
| 102 | Резерв | 1 |
|
6. СРЕДСТВА КОНТРОЛЯ
В ходе реализации данной программы предусмотрены следующие виды и формы контроля: самостоятельные работы, тестирование, математические диктанты, контрольные работы. Формы учёта достижений это: проверка тетрадей по предмету, анализ текущей успеваемости, внеурочная деятельность- участие в олимпиадах, математических конкурсах.
7. УЧЕБНО – МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ .
Алгебра-9:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2004 – 2007 год.
Изучение алгебры в 7—9 классах/ Ю. Н. Макарычев, Н.Г. Миндюк, С.Б. Суворова..— М.: Просвещение, 2005—2008.
Уроки алгебры в 9 классе: кн. для учителя / В.И. Жохов, Л.Б. Крайнева. — М.: Просвещение, 2005— 2008.
Алгебра: дидакт. материалы для 9 кл. / Л. И. Звавич, Л. В. Кузнецова, С. Б» Суворова. — М.: Просвещение, 2007—2008
Поурочные разработки по алгебре.(к учебнику Ю.Н.Макарычева и др.) А.Н. Рурукин, С.А. Полякова.Москва, «ВАКО», 2010.
Математика, 2012. ГИА 9. А.В.Семенов, А.С. Трепалин, И.В.Ященко, П.И.Захаров. Москва,»Интеллект-Центр» 2012.
Учебно-методический комплекс ученика:
Алгебра-9:учебник/автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова, Просвещение, 2004 – 2007 год. 5
Алгебра: дидактические материалы для 9 класса. Ю.Н.Макарычев, Н.Г. Миндюк, Л.Б.Крайнева, Москва, Просвещение, 2011.
Математика, 2012.ГИА 9. А.В.Семенов, А.С.Трепалин, И.В.Ященко, П.И.Захаров. Москва,»Интеллект- Центр», 2012.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре (9 класс) (0.26 MB)
Рабочая программа по алгебре (9 класс) (0.26 MB)
 0
0 626
626 98
98 Нравится
0
Нравится
0





