МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ГИМНАЗИЯ №4 ГОРОДСКОГО ОКРУГА САМАРА
| «Утверждаю» Приказ №________ от ___________2015г. | «Согласовано» | «Рассмотрено на заседании МО физико-математического цикла» Протокол №__ от _____2015г. |
| Директор гимназии _________________ | Заместитель директора по УВР __________________ | Председатель МО ________________________ |
Рабочая программа предмета
«Математика»
для 5 - 6 классов,
уровня основного общего образования
Общее количество часов на уровень: 340
Количество часов в год по учебному плану:
5 класс – 170 часов
6 класс – 170 часов
Уровень реализации образовательной программы: базовый
Разработана на основе Рабочей программы. Предметная линия учебников «Сферы». 5-6 классы: пособие для учителей общеобразовательных учреждений / Л.В. Кузнецова, С.С. Минаева,
Л.О. Рослова, С.Б. Суворова. - М.: Просвещение, 2011.
Составил учитель математики *******
САМАРА, 2015
Используемый учебно-методический комплект:
Математика. Арифметика. Геометрия. Поурочное тематическое планирование. 5 класс: пособие для учителей общеобразовательных учреждений под ред. Л.В. Кузнецова, С.С. Минаева и др. – М.: Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012г.
Математика. Арифметика. Геометрия. 5 класс: тетрадь - тренажер, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 5 класс: задачник - тренажер, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 5 класс: тетрадь - экзаменатор, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Электронное приложение к учебнику 5 класса (СD-ROM)
Математика. Арифметика. Геометрия. Поурочное тематическое планирование. 6 класс: пособие для учителей общеобразовательных учреждений под ред. Л.В. Кузнецова, С.С. Минаева и др. – М.: Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 6 класс: учебник для общеобразовательных учреждений, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 6 класс: тетрадь - тренажер, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 6 класс: задачник - тренажер, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Математика. Арифметика. Геометрия. 6 класс: тетрадь - экзаменатор, под ред. Е.А. Буминович, С.Б. Суровова. – М. – Просвещение, 2012 г.
Электронное приложение к учебнику 6 класса (СD-ROM).
Кроме того, на сайте интернет-поддержки УМК «Сферы» www.spheres.ru имеется страничка данного УМК.
Пояснительная записка к рабочей программе по курсу
«Математика»
для 5 - 6 классов,
уровня основного общего образования
Общая характеристика учебного предмета, курса:
В Федеральном государственном образовательном стандарте и Примерной программе основного общего образования сформулированы цели образования в основной школе и требования к результатам освоения содержания курса. Эти целевые установки носят общий характер и задают направленность обучения математике в основной школе в целом. В данной рабочей программе они конкретизированы применительно к этапу 5-6 классов с учетом возрастных возможностей учащихся. В качестве приоритетных выдвигаются следующие цели:
подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, пониманию математики как части общей культуры человечества;
развитие познавательной активности; формирование мыслительных операций, являющихся основой интеллектуальной деятельности; развитие логического мышления, алгоритмического мышления; формирование умения точно выразить мысль;
развитие интереса к математике, математических способностей;
формирование знаний и умений, необходимых для изучения курсов математики 7-9 классов, смежных дисциплин, применения в повседневной жизни.
В данной рабочей программе курс 5-6 классов линии УМК «Сферы» представлен как арифметико-геометрический с включением элементов алгебры. Кроме того, к нему отнесено начало изучения вероятностно-статистической линии, а также элементов раздела «Логика и множества», возможность чего предусмотрена Примерной программой по математике для 5-9 классов.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения математики и смежных предметов, способствует развитию логического мышления учащихся, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. При изучении арифметики формирование теоретических знаний сочетается с развитием вычислительной культуры, которая актуальна и при наличии вычислительной техники, в частности, с обучением простейшими приемами прикидки и оценки результатов вычислений. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел. Параллельно на доступном для учащихся данного возраста уровня в курсе представлена научная идея – расширение понятия числа.
В задачи изучения раздела «Геометрия» входит развитие геометрических представлений учащихся, образного мышления, пространственного воображения, изобразительных умений. Этот этап изучения геометрии осуществляется в 5-6 классах на наглядно-практическом уровне, при этом большая роль отводится опыту, эксперименту. Учащиеся знакомятся с геометрическими фигурами и базовыми конфигурациями, овладевают приемами построения, открывают их свойства, применяют эти свойства при решении задач конструктивного и вычислительного характера.
Изучение раздела «Алгебра» в основной школе предполагает овладение формальным аппаратом буквенного исчисления. Это материал более высокого, нежели арифметика уровня абстракции. Его изучение решает целый ряд методологического, мировоззренческого, личностного характера, но в то же время требует определённого уровня интеллектуального развития. Поэтому в курсе 5-6 классов представлены только начальные, базовые понятия, и он играет роль своего рода мостика между арифметикой и алгеброй, назначение которого можно образно описать так: от чисел к буквам.
Изучение раздела «Вероятность и статистика» вносит существенный вклад в осознание учащимися прикладного и практического значения математики. В задачи его изучения входит формирование умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, оценивать вероятность наступления события. Основное содержание этого раздела отнесено к 7-9 классам. Для курса 5-6 классов выделены следующие вопросы: формирование умения работать с информацией, представленной в форме таблиц и диаграмм, первоначальных знаний о приемах сбора и представления информации, первое знакомство с комбинаторикой, решение комбинаторных задач.
Введение в курс элементарных теоретико–множественных понятий и соответствующей символики способствует обогащению математического языка школьников, формированию умения точно и сжато формулировать математические предложения, помогает обобщению и систематизации знаний.
В содержание основного общего образования, предусмотренного Примерными программами по математике для 5-9 классов, включен также раздел «Математика в историческом развитии». Его элементы представлены и в содержании курса 5-6 классов. Назначение этого материала состоит в создании гуманитарного, культурно – исторического фона при рассмотрении проблематики основного содержания.
Описание места и роли учебного курса, предмета в учебном плане:
Информация о внесенных изменениях в примерную или авторскую программу и их обоснование
В соответствии с учебным планом основного общего образования в курсе математики выделяют два этапа – 5 – 6 классы и 7-9 классы, у каждого из которых свои самостоятельные функции. В 5-6 классах изучается интегрированный предмет «Математика», в 7-9 классах – два предмета «Алгебра» и «Геометрия». Курс 5-6 классов, с одной стороны является непосредственным продолжением курса математики начальной школы, систематизирует, обобщает и развивает полученные там знания, с другой стороны, позволяет учащимся адаптироваться к новому уровню изучения предмета, создать необходимую основу, на которой будут базироваться систематические курсы 7-9 классов. На изучение математики в основной школе отводится 5 часов в неделю в течение всех лет обучения. По программе Предметная линия учебников «СФЕРЫ» 5-6 классы на интегрированный курс «Математика» в 5-6 классах всего отводится 350 уроков. В соответствии с годовым календарным графиком работы МБОУ Гимназии №4 г.о. Самара 34 учебных недели. Данная программа рассчитана на 340 часов, в том числе в 5, 6 классах 170 часов, из расчета 5 учебных часа в неделю. Уменьшение часов рабочей программы на 10 проведено за счет часов резерва свободного времени: было 20 стало 10 учебных часов и не влечет за собой уменьшение объема содержания программы.
Нормативные правовые документы, на основании которых разработана рабочая программа:
Федеральный государственный образовательный стандарт основного общего образования, утвержденный приказом Министерства образования и науки Российской Федерации, №1897 от 17.12.2010 г.
Основная образовательная программа основного общего образования МБОУ Гимназии № 4 г.о. Самара.
Примерные программы по учебным предметам. Математика. 5-9 классы. М.: Просвещение, 2011 г.
Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова, С.Б. Суворова. Математика. Рабочие программы. Предметная линия учебников «Сферы». 5-6 классы. М.: Просвещение, 2011
Цели, достигаемые при реализации рабочей программы
К важнейшим результатам обучения математике в 5-6 классах при преподп=авании по УМК «Сферы» относятся следующие:
В личностном направлении:
знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии из практических потребностей людей);
способность к эмоциональному восприятию математических объектов, решений задач, рассматриваемых проблем;
умение строить речевые конструкции (устные и письменные) с использованием изученной терминологии символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот.
В метапредметном направлении:
умение планировать свою деятельность при решении учебных математических задач, видеть различные стратегии решения задач, осознанно выбирать способ решения;
умение работать с учебным математическим текстом (находить ответы на поставленные вопросы, выделять смысловые фрагменты и пр.);
умение проводить несложные доказательные рассуждения, опираясь на изученные определения, свойства, признаки; распознавать верные и неверные утверждения; иллюстрировать примерами изученные понятия и факты, опровергать с помощью контрпримеров неверные утверждения;
уметь действовать в соответствии с предложенным алгоритмом, составлять несложные алгоритмы вычислений и построений;
применение приемов самоконтроля при решении учебных задач;
умение видеть математическую задачу в несложных практических ситуациях;
В предметном направлении:
владение базовым понятийным аппаратом по основным разделам содержания;
владение навыками вычислений с натуральными числами, обыкновенными и десятичными дробями, положительными и отрицательными числами;
умение решать текстовые задачи арифметическим способом, используя различные стратегии и способы рассуждения;
усвоение на наглядном уровне знаний о свойствах плоских и пространственных фигур; приобретение навыков их изображения; умение использовать геометрический язык для описания предметов окружающего мира;
приобретение опыта измерения длин отрезков, величин углов, вычисления площадей и объемов; понимание идеи измерения длин, площадей, объемов;
знакомство с идеями равенства фигур, симметрии; умение распознавать равные и симметричные фигуры;
умение проводить несложные практические расчеты (включающие вычесления с процентами, выполнение необходимых измерений, использование прикидки и оценки);
использование букв для записи общих утверждений, формул, выражений, уравнений; умение оперировать понятием «буквенное выражение», осуществлять элементарную деятельность, связанную с понятием «уравнения»;
знакомство с идеей координат на прямой и плоскости; выполнение стандартных процедур на координатной плоскости;
понимание и использование информации, представленной в форме таблицы, столбчатой или круговой диаграммы;
Умение решать простейшие комбинаторные задачи перебором возможных вариантов.
Планируемый уровень подготовки выпускников на конец ступени
Выпускник научится в 5-6 классах (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)
Оперировать на базовом уровне понятиями: множество, элемент множества, подмножество, принадлежность;
задавать множества перечислением их элементов;
находить пересечение, объединение, подмножество в простейших ситуациях.
В повседневной жизни и при изучении других предметов:
Числа
Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число;
использовать свойства чисел и правила действий с рациональными числами при выполнении вычислений;
использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;
выполнять округление рациональных чисел в соответствии с правилами;
сравнивать рациональные числа.
В повседневной жизни и при изучении других предметов:
оценивать результаты вычислений при решении практических задач;
выполнять сравнение чисел в реальных ситуациях;
составлять числовые выражения при решении практических задач и задач из других учебных предметов.
Статистика и теория вероятностей
Представлять данные в виде таблиц, диаграмм,
читать информацию, представленную в виде таблицы, диаграммы.
Текстовые задачи
Решать несложные сюжетные задачи разных типов на все арифметические действия;
строить модель условия задачи (в виде таблицы, схемы, рисунка), в которой даны значения двух из трех взаимосвязанных величин, с целью поиска решения задачи;
осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;
составлять план решения задачи;
выделять этапы решения задачи;
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
знать различие скоростей объекта в стоячей воде, против течения и по течению реки;
решать задачи на нахождение части числа и числа по его части;
решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;
находить процент от числа, число по проценту от него, находить процентное отношение двух чисел, находить процентное снижение или процентное повышение величины;
решать несложные логические задачи методом рассуждений.
В повседневной жизни и при изучении других предметов:
Наглядная геометрия
Геометрические фигуры
Оперировать на базовом уровне понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырехугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар. Изображать изучаемые фигуры от руки и с помощью линейки и циркуля.
В повседневной жизни и при изучении других предметов:
Измерения и вычисления
выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
вычислять площади прямоугольников.
В повседневной жизни и при изучении других предметов:
История математики
описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей.
Выпускник получит возможность научиться в 5-6 классах (для обеспечения возможности успешного продолжения образования на базовом и углубленном уровнях)
Элементы теории множеств и математической логики
Оперировать1 понятиями: множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность,
определять принадлежность элемента множеству, объединению и пересечению множеств; задавать множество с помощью перечисления элементов, словесного описания.
В повседневной жизни и при изучении других предметов:
Числа
Оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, геометрическая интерпретация натуральных, целых, рациональных;
понимать и объяснять смысл позиционной записи натурального числа;
выполнять вычисления, в том числе с использованием приемов рациональных вычислений, обосновывать алгоритмы выполнения действий;
использовать признаки делимости на 2, 4, 8, 5, 3, 6, 9, 10, 11, суммы и произведения чисел при выполнении вычислений и решении задач, обосновывать признаки делимости;
выполнять округление рациональных чисел с заданной точностью;
упорядочивать числа, записанные в виде обыкновенных и десятичных дробей;
находить НОД и НОК чисел и использовать их при решении зада;.
оперировать понятием модуль числа, геометрическая интерпретация модуля числа.
В повседневной жизни и при изучении других предметов:
применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;
выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений;
составлять числовые выражения и оценивать их значения при решении практических задач и задач из других учебных предметов.
Уравнения и неравенства
Оперировать понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство.
Статистика и теория вероятностей
Оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое,
извлекать, информацию, представленную в таблицах, на диаграммах;
составлять таблицы, строить диаграммы на основе данных.
В повседневной жизни и при изучении других предметов:
извлекать, интерпретировать и преобразовывать информацию, представленную в таблицах и на диаграммах, отражающую свойства и характеристики реальных процессов и явлений.
Текстовые задачи
Решать простые и сложные задачи разных типов, а также задачи повышенной трудности;
использовать разные краткие записи как модели текстов сложных задач для построения поисковой схемы и решения задач;
знать и применять оба способа поиска решения задач (от требования к условию и от условия к требованию);
моделировать рассуждения при поиске решения задач с помощью граф-схемы;
выделять этапы решения задачи и содержание каждого этапа;
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях;
исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчета;
решать разнообразные задачи «на части»,
решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;
осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение); выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задачи указанных типов.
В повседневной жизни и при изучении других предметов:
выделять при решении задач характеристики рассматриваемой в задаче ситуации, отличные от реальных (те, от которых абстрагировались), конструировать новые ситуации с учетом этих характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества;
решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
решать задачи на движение по реке, рассматривая разные системы отсчета.
Наглядная геометрия
Геометрические фигуры
Извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
изображать изучаемые фигуры от руки и с помощью компьютерных инструментов.
Измерения и вычисления
выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
вычислять площади прямоугольников, квадратов, объемы прямоугольных параллелепипедов, кубов.
В повседневной жизни и при изучении других предметов:
вычислять расстояния на местности в стандартных ситуациях, площади участков прямоугольной формы, объемы комнат;
выполнять простейшие построения на местности, необходимые в реальной жизни;
оценивать размеры реальных объектов окружающего мира.
История математики
Содержание курса математики в 5–6 классах
Натуральные числа и нуль
Натуральный ряд чисел и его свойства
Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками на числовой прямой. Использование свойств натуральных чисел при решении задач.
Запись и чтение натуральных чисел
Различие между цифрой и числом. Позиционная запись натурального числа, поместное значение цифры, разряды и классы, соотношение между двумя соседними разрядными единицами, чтение и запись натуральных чисел.
Округление натуральных чисел
Необходимость округления. Правило округления натуральных чисел.
Сравнение натуральных чисел, сравнение с числом 0
Понятие о сравнении чисел, сравнение натуральных чисел друг с другом и с нулем, математическая запись сравнений, способы сравнения чисел.
Действия с натуральными числами
Сложение и вычитание, компоненты сложения и вычитания, связь между ними, нахождение суммы и разности, изменение суммы и разности при изменении компонентов сложения и вычитания.
Умножение и деление, компоненты умножения и деления, связь между ними, умножение и сложение в столбик, деление уголком, проверка результата с помощью прикидки и обратного действия.
Переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, обоснование алгоритмов выполнения арифметических действий.
Степень с натуральным показателем
Запись числа в виде суммы разрядных слагаемых, порядок выполнения действий в выражениях, содержащих степень, вычисление значений выражений, содержащих степень.
Числовые выражения
Числовое выражение и его значение, порядок выполнения действий.
Деление с остатком
Деление с остатком на множестве натуральных чисел, свойства деления с остатком. Практические задачи на деление с остатком.
Свойства и признаки делимости
Свойство делимости суммы (разности) на число. Признаки делимости на 2, 3, 5, 9, 10. Признаки делимости на 4, 6, 8, 11. Доказательство признаков делимости. Решение практических задач с применением признаков делимости.
Разложение числа на простые множители
Простые и составные числа, решето Эратосфена.
Разложение натурального числа на множители, разложение на простые множители. Количество делителей числа, алгоритм разложения числа на простые множители, основная теорема арифметики.
Алгебраические выражения
Использование букв для обозначения чисел, вычисление значения алгебраического выражения, применение алгебраических выражений для записи свойств арифметических действий, преобразование алгебраических выражений.
Делители и кратные
Делитель и его свойства, общий делитель двух и более чисел, наибольший общий делитель, взаимно простые числа, нахождение наибольшего общего делителя. Кратное и его свойства, общее кратное двух и более чисел, наименьшее общее кратное, способы нахождения наименьшего общего кратного.
Дроби
Обыкновенные дроби
Доля, часть, дробное число, дробь. Дробное число как результат деления. Правильные и неправильные дроби, смешанная дробь (смешанное число).
Запись натурального числа в виде дроби с заданным знаменателем, преобразование смешанной дроби в неправильную дробь и наоборот.
Приведение дробей к общему знаменателю. Сравнение обыкновенных дробей.
Сложение и вычитание обыкновенных дробей. Умножение и деление обыкновенных дробей.
Арифметические действия со смешанными дробями.
Арифметические действия с дробными числами.
Способы рационализации вычислений и их применение при выполнении действий.
Десятичные дроби
Целая и дробная части десятичной дроби. Преобразование десятичных дробей в обыкновенные. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Округление десятичных дробей. Умножение и деление десятичных дробей. Преобразование обыкновенных дробей в десятичные дроби. Конечные и бесконечные десятичные дроби.
Отношение двух чисел
Масштаб на плане и карте. Пропорции. Свойства пропорций, применение пропорций и отношений при решении задач.
Среднее арифметическое чисел
Среднее арифметическое двух чисел. Изображение среднего арифметического двух чисел на числовой прямой. Решение практических задач с применением среднего арифметического. Среднее арифметическое нескольких чисел.
Проценты
Понятие процента. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах. Решение несложных практических задач с процентами.
Диаграммы
Столбчатые и круговые диаграммы. Извлечение информации из диаграмм. Изображение диаграмм по числовым данным.
Рациональные числа
Положительные и отрицательные числа
Изображение чисел на числовой (координатной) прямой. Сравнение чисел. Модуль числа, геометрическая интерпретация модуля числа. Действия с положительными и отрицательными числами. Множество целых чисел.
Понятие о рациональном числе. Первичное представление о множестве рациональных чисел. Действия с рациональными числами.
Решение текстовых задач
Единицы измерений: длины, площади, объема, массы, времени, скорости. Зависимости между единицами измерения каждой величины. Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость.
Задачи на все арифметические действия
Решение текстовых задач арифметическим способом. Использование таблиц, схем, чертежей, других средств представления данных при решении задачи.
Задачи на движение, работу и покупки
Решение несложных задач на движение в противоположных направлениях, в одном направлении, движение по реке по течению и против течения. Решение задач на совместную работу. Применение дробей при решении задач.
Задачи на части, доли, проценты
Решение задач на нахождение части числа и числа по его части. Решение задач на проценты и доли. Применение пропорций при решении задач.
Логические задачи
Решение несложных логических задач. Решение логических задач с помощью графов, таблиц.
Основные методы решения текстовых задач: арифметический, перебор вариантов.
Наглядная геометрия
Фигуры в окружающем мире. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Изображение основных геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Единицы измерения длины. Построение отрезка заданной длины. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира.
Периметр многоугольника. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Приближенное измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры разверток многогранников, цилиндра и конуса.
Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
Решение практических задач с применением простейших свойств фигур.
История математики
Появление цифр, букв, иероглифов в процессе счета и распределения продуктов на Древнем Ближнем Востоке. Связь с Неолитической революцией.
Рождение шестидесятеричной системы счисления. Появление десятичной записи чисел.
Рождение и развитие арифметики натуральных чисел. НОК, НОД, простые числа. Решето Эратосфена.
Появление нуля и отрицательных чисел в математике древности. Роль Диофанта. Почему 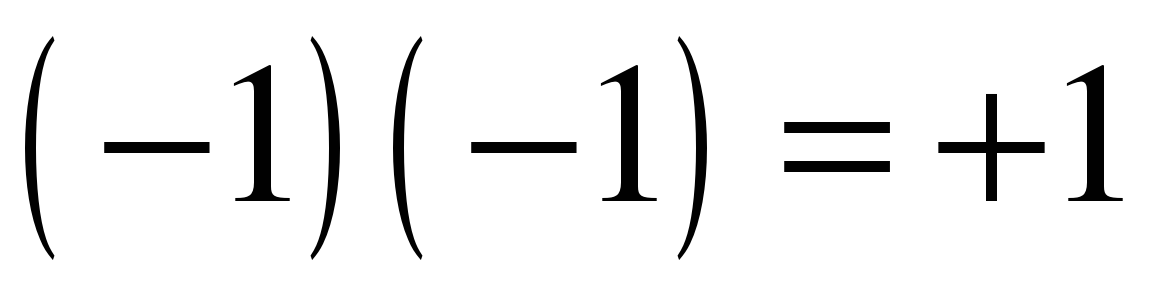 ?
?
Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Л. Магницкий.
1


 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа предмета «Математика» (0.12 MB)
Рабочая программа предмета «Математика» (0.12 MB)
 0
0 1296
1296 54
54 Нравится
0
Нравится
0










