МАОУ СОШ №4 г. Боровичи Новгородской области
Сборник заданий
на развитие мышления
младших школьников на уроках математики
Составители:
учитель начальных классов
1 квалификационной категории
Ильченко В.А.
учитель начальных классов
Терентьева О.Е.
учитель начальных классов
Сараева Н.П.
г. Боровичи
В пособие включены систематизированные задания для развития мышления младших школьников, которые можно включать на уроках математики.
Пособие содержит логические цепочки, нетрадиционные задания и упражнения, направленные на развитие мыслительных операций. Отдельный раздел посвящен логическим задачам. В сборник также входят задачи со сказочным сюжетом. Все задания, которые включены в этот сборник позволяют разнообразить учебный процесс и сформировать у детей навыки логического мышления. Может быть использовано учителями начальной школы, работающими с детьми младшего школьного возраста и родителям младших школьников.
Введение
Пространственное мышление - это база, на которой строится большая часть учебной и впоследствии трудовой деятельности человека, поэтому развитие и формирование этого вида умственной активности очень важно для профессиональной успешности личности.
Особенно это стало актуальным в период современности, когда возросла роль схематичности, графических изображений, условных обозначений.
Формирование пространственного мышления происходит поэтапно, затрагивая все периоды формирования человека:
Начальная форма ориентирования появляется в раннем возрасте, когда у младенца выстраивается связь между анализаторами - слуховыми, зрительными и двигательными;
Осознание своего положения относительно пространства формируется к трехлетнему возрасту;
До семи лет получают свое развитие первые представления об окружающем пространстве;
Формирование восприятия пространства в виде системы происходит через обучение на уроках математики и геометрии в младшем школьном возрасте.
Каждый из этих этапов, помимо первого, получает свое развитие в деятельности игровой и учебной, поэтому родителям и учителям важно не упустить время, когда есть возможность максимально эффективно сформировать восприятие пространства и ориентацию в нем.
Реализация задачи по формированию пространственного мышления у учащихся начальных классов на примере 1 класса.
Исследования, проводимые учеными в школах с детьми 6-10 лет, показывают, что гипотеза о необходимости увеличения объема знаний математики и геометрии в начальной школе верна, на этих уроках происходит:
• Увеличение количества геометрических представлений, начало которых было заложено у дошкольников;
• У школьников младших классов - формирование плоскостного и пространственного воображения;
• Формируются простейшие геометрические понятия;
• Развитие способности к использованию различных фигур из геометрии (круг, многоугольник, отрезок) в качестве базы, когда формируются представления о долях величин и решается тест;
• Закладывание основ умения мыслить посредством геометрических методов: сравнение, анализ, рассуждение, выводы и т.п.;
• Заложение основ способности к конструированию;
• Развитие потенциала к творчеству и созданию нового.
У младших школьников методы развития восприятия пространства достаточно универсальны и основываются на выполнении задач на уроках математики.
Для того, чтобы грамотно и поэтапно ввести ребенка в мир математических и геометрических законов, требуется использовать изначальный опыт ориентации в пространстве, который формируется посредством взаимодействия с различными предметами, оперирования геометрическими формами, игровой и трудовой деятельности на уроках.
Задания на развитие мышления
Нетрадиционные задания, задачи и упражнения направлены на развитие практически всех мыслительных операций.
Большой наблюдательности требует от учащихся логические цепочки, которые нужно продолжить вправо и влево, если такое возможно. Чтобы выполнить задание, необходимо установить закономерности в записи чисел:
1. Логические цепочки:
… 5 7 9… (Ответ: 1,3,5, 7, 9, 11, 13).
… 5 6 9 10 … ( Ответ: 1, 2, 5, 6, 9, 10, 13, 14).
….21 17 13 …. (Ответ: 29, 25, 21, 17, 13, 14).
1 4 7 ….. (Ответ: 1, 4, 7, 10, 13, 16,….).
6 12 18…… ( Ответ: 6, 12, 18, 24, 30, 36,…).
2. Игра «Лишнее число».
Даны числа: 1, 10, 6. Какое число лишнее?
Лишним может быть число 1, так как это нечетное число, а 10 и 6 четное. Даже лишним может быть число 10, так как оно двузначное, а 1 и 6 однозначные. Да и число 6 может быть лишним, так как для написания двух других использована единица.
Сравнивать можно не только числа, но и математические выражения.
Даны примеры: 3 + 4 и 1 + 6.
На первый взгляд нет ничего общего кроме знака действия. Но, внимательно присмотревшись, можно заметить, что первые слагаемые меньше вторых, первые слагаемые – нечетные, а вторые – четные.
Можно предложить детям составить аналогичную пару примеров на вычитание, деление или умножение.
Развитию логического мышления способствуют задания, которые можно назвать: 3. «Ошибки – невидимки».
Учитель на доске, а родители, занимающиеся с ребёнком в альбоме или тетради записывают несколько математических выражений содержащих явную ошибку. Задача учащихся, ничего, не стирая и не справляя, сделать ошибку невидимой. Дети должны дать разные варианты исправления ошибок.
Задания и варианты исправления ошибок:
10
8 = 7 15 -8 =7 8= 7 + 1
6 + 3 = 10 6 + 3 = 10 – 1 1 + 6 + 3 = 10
Развитию мышления способствуют также задания по классификации:
4. Задание. Числа разбиты на группы. Надо указать основание классификации.
а) 5,8 и 14, 17, 26, 32 (Ответ: однозначные и двузначные числа).
б)5, 14 , 32 и 8, 17, 26 (Ответ: сумма цифр чисел первой группы равна 5, сумма цифр чисел второй группы равна 8).
в) 5, 17 и 8, 14, 26, 32 (Ответ: группы четных и нечетных чисел).
5. Задание. (на классификацию)
Найди лишнее число и объясни, почему оно лишнее: 135, 450, 258, 63, 711.
Сколько вариантов решения?
(Ответ: 450 – лишнее число, так как оно круглое;
63 – лишнее число, так как оно двузначное;
711 – лишнее число, так как для записи этого числа используется цифра 1, которая повторяется 2 раза;
258 – лишнее число, так как в остальных числах сумма цифр числа равна 9)
6. Задание ( на классификацию)
Какое выражение можно назвать лишним?
1 + 3 + 2, 1 + 5, 7- 1, 2 + 4, 6 –4, 3 +3.
(Ответ: 1+3+2 – больше действий;
6 – 4 – так как результат равен 2;
7-1 – целое равно 7, а в остальных выражениях 6;
3 + 3 – сумма состоит из одинаковых слагаемых.)
7.Задание (на классификацию).
Рассмотрите ряды чисел: 2 4 6 8
1 2 3 4
1 3 5 7
Какой из них можно назвать лишним?
(Ответ: Лишним является второй ряд, так как в нём числа идут последовательно друг за другом в порядке возрастания. В первом и третьем рядах последовательно увеличиваются на 2.)
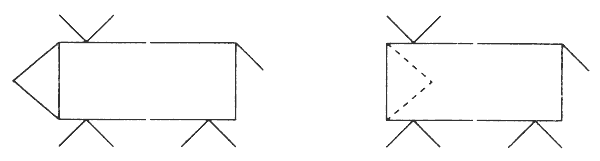
8 Дана фигура, похожая на стрелу. Надо переложить 4 палочки так, чтобы получилось 4 треугольника.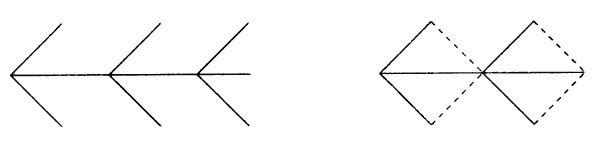
9. Поставь одинаковые цифры так, чтобы получилось верное равенство:
1* + 3* + 5* = 111.
(Ответ : 17 + 37 + 57 = 111.)
10. Задачи на составление заданной фигуры из определенного количества палочек.
Задачи на изменение фигур, для решения которых надо убрать указанное количество палочек.
Дана фигура из 6 квадратов. Надо убрать 2 палочки так, чтобы осталось 4 квадрата.
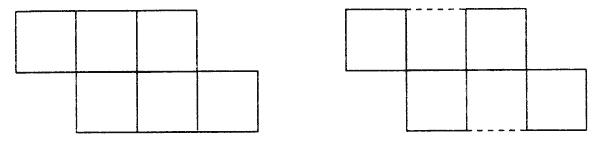
11. Сколько различных букв в словах УРА КЕНГУРУ? (Ответ: 7 букв.)
Магические квадраты.
В девяти клетках квадрата расположите числа 2, 2, 2, 4,4, 4, 6, 6,6 так, чтобы сумма чисел по горизонтали, вертикали и диагоналям была равна 12.
| 2 | 6 | 4 |
| 6 | 4 | 2 |
| 4 | 2 | 6 |
В девяти клетках квадрата, в центре которого стоит число 4, расставьте числа 0,1,2,3,4,5,6,7,8 так, чтобы сумма по горизонтали, вертикали и диагоналям была равна 12.
|
|
|
|
|
| 4 |
|
|
|
|
|
| 3 | 8 | 1 |
| 2 | 4 | 6 |
| 7 | 0 | 5 |
Ответ:
В шестнадцати клетках квадрата расставьте числа 1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4. Числа надо расставить так, чтобы сумма по горизонтали, вертикали и диагоналям была равна 10.
| 1 | 4 | 4 | 1 |
| 3 | 2 | 2 | 3 |
| 2 | 3 | 3 | 2 |
| 4 | 1 | 1 | 4 |
В шестнадцати клетках квадрата расставьте числа 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. Числа надо расставить так, чтобы сумма по горизонтали, вертикали и диагоналям была равна 30.
| 0 | 14 | 13 | 3 |
| 11 | 5 | 6 | 8 |
| 7 | 9 | 10 | 4 |
| 12 | 2 | 1 | 15 |
В двадцати пяти клетках квадрата расставьте числа 1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5. Числа надо расставить так, чтобы сумма по горизонтали, вертикали и диагоналям была равна 15.
| 1 | 4 | 2 | 5 | 3 |
| 4 | 2 | 5 | 3 | 1 |
| 2 | 5 | 3 | 1 | 4 |
| 5 | 3 | 1 | 4 | 2 |
| 3 | 1 | 4 | 2 | 5 |
В двадцати пяти клетках квадрата расставьте числа от 1 до 25. Числа надо расставить так, чтобы сумма по горизонтали, вертикали и диагоналям была равна 65.
| 11 | 14 | 7 | 20 | 3 |
| 4 | 12 | 25 | 8 | 16 |
| 17 | 5 | 13 | 21 | 9 |
| 10 | 18 | 1 | 14 | 22 |
| 23 | 6 | 19 | 2 | 15 |
Заполните числами магический квадрат, чтобы сумма по горизонтали, вертикали и диагоналям была равна 63.
|
|
| |||||||||
|
| 21 |
| |||||||||
|
| 1 | 26 |
Ответ:
Заполните числами магический квадрат, чтобы сумма по горизонтали, вертикали и диагоналям была равна 30.
4 | 14 | 12 | |||||||||
| 18 | 10 | 2 | |||||||||
| 8 | 6 | 16 |
Ответ:
12. Сколько месяцев в году имеют 28 дней?
(Ответ: Все 12, т. к. если в месяце 30 дней, то и 28 среди них есть.)
13. Какие часы показывают время верное только два раза в сутки?
(Ответ: которые остановились.)
14. Задачи, решение которых состоит в перекладывании палочек с целью видоизменения фигуры.
Составить домик из 6 палочек, а затем переложить 2 палочки так, чтобы, получился флажок.

В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника
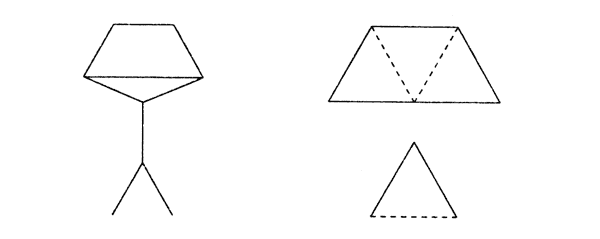
Переложить 6 палочек так, чтобы, из корабля получился танк.
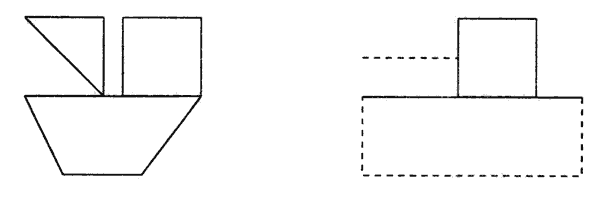
Переложить 2 палочки так, чтобы фигура, похожая на корову, смотрела в другую сторону.
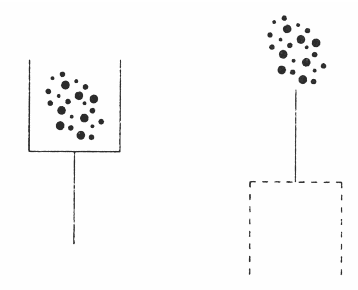
Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка?
15. В ребусе КЕН × Г = УРУ одинаковыми буквами зашифрованы одинаковые цифры, а разными – разные. Если К равно 2, то У равно
(А) 4 (Б) 6 (В) 7 (Г) 8 (Д) 9
(Ответ: У=8. 217 ×4 = 868.)
16. Задание на классификацию.
Перед вами ряд фигур (предметов). Если бы необходимо было разделить их на группы, то как это можно сделать?
Набор фигур.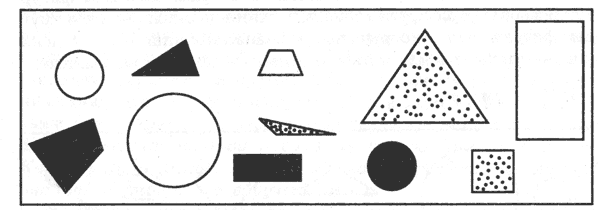
(Ответ: Важно, чтобы ребенок, выполняя это задание, нашел как можно больше оснований для классификации. Например, это может быть классификация по форме, цвету, размеру; деление на 3 группы: круглые, треугольники, четырехугольники, или 2 группы: белые и не белые и т.д.)
Занимательные задачи со сказочным сюжетом
Задачи со сказочным сюжетом очень нравятся детям. Являясь занимательными по форме, они усиливают интерес к самой задаче, побуждают ребенка решать проблему, вызывают желание помочь полюбившимся героям.
Очень важно подобрать посильные для учеников задания, соответствующие их возможностям, развитию. Ведь часто бывает, что даже смышленый ученик не хочет просто прочитать задачу, не то что решать ее, а поэтому целесообразно использовать внешнюю занимательность текстов. Цель может быть достигнута, если условие задачи будет похоже на сказку.
Задача. Кто победил Змея Горыныча?
- Змей Горыныч побежден! – такая молва дошла до Микулы Селяниновича. Он знал, что это мог сделать кто-то из богатырей: либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле Селяниновичу сообщили:
(А) Змея Горыныча победил не Илья Муромец;
(Б) Змея Горыныча победил Алеша Попович.
Спустя некоторое время выяснилось, что одно из этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
(Ответ: Змея Горыныча победил Добрыня Никитич.
Предположим, что Змея Горыныча победил Илья Муромец. Тогда оба сообщения неверные – результат не соответствует условию задачи.
Предположим, что Змея Горыныча победил Алеша Попович. Тогда оба сообщения верные. И этот результат условию задачи не соответствует.
Предположим, что Змея Горыныча победил Добрыня Никитич. Тогда первое сообщение верное, а второе неверное. Результат соответствует условию задачи.)
Задача «Отряд солдат»
Отряд солдат подходит к реке, через которую надо переправиться. Но мост сломан, а река глубока. Как быть? Вдруг командир замечает двух мальчиков, которые катаются на лодке недалеко от берега. Но лодка так мала, что может выдержать одного солдата или только двух мальчиков - не больше! Однако все солдаты переправились через реку именно на этой лодке. Как это было сделано?
21
(Ответ: Дети переправились через реку. Один из мальчиков остался на берегу, а другой пригнал лодку к солдатам и вылез. Тогда сел солдат и переправился на другой берег. Мальчик, оставшийся там, пригнал лодку обратно, взял своего товарища, отвёз его на другой берег и снова доставил лодку обратно, после чего вылез, и в неё сел другой солдат и переправился. Таким образом, после двух перегонов лодки через реку и обратно переправлялся один солдат.)
Задача «Режим дня для попрыгуньи Стрекозы»
Попрыгунья Стрекоза половину времени каждых суток красного лета спала, третью часть каждых суток танцевала, шестую часть – пела. Остальное время она решила посвятить подготовке к зиме. Сколько часов в сутки Стрекоза готовилась к зиме?
( Ответ: На подготовку к зиме у стрекозы совсем не хватало времени.
В сутках 24 часа. Из них Стрекоза спала 24 : 2 = 12(ч),
танцевала 24 : 3 =8(ч), пела 24 : 6 = 4(ч). Всего она на эти дела тратила 12 + 8+ 4 = 24 (ч). Как видим в течение суток Стрекоза ни часу не готовилась к зиме.)
Наловил дед рыбы полный воз и прилёг отдохнуть. Мимо шёл Кот Котофеевич, и стал он рыбку есть. Сначала Котофеевич действовал осторожно, а затем смелее. В первую минуту он съел одного леща, во вторую два леща, в третью – четыре леща и так далее: в каждую следующую минуту он съел вдвое больше лещей. Через семь минут Котофеевич съел всю рыбу. Сколько лещей поймал дед?
( Ответ: 1 + 2 + 4 + 8+ 16 + 32 + 64 = 127.)
Задача «Индейский кросс.
Индейцы Азии, Биг, Вики
И долговязый Гили
На берегу Олень – реки
Устроить кросс решили.
Старт был у камня, где родник,
А финиш там, где сети.
Прошу, запомните, что Биг.
Не первый и не третий.
В таблице Азии от Вики
Два места отделяли.
(Ура, Вики!) На две строки
Биг выше встал, чем Гили.
Теперь прошу карандашом
Скорей вооружиться.
Подумать надо хорошо,
И сложиться таблица.
(Ответ: 1 – Вики, 2 – Биг, 3 – Азии, 4 – Гили.)
Задача. Иван против Кощея Бессмертного.
- Помогу тебе, Иван, вызволить Василису Прекрасную, - сказала Баба Яга. – По душе ты мне пришелся. Да и от Кощеева коварства много я страдала, уж очень хочется его проучить.
Вот тебе, Иван, клубок. Приведет он тебя прямо к Кощею Бессмертному. В подземелье у него три темницы. В одной из них томится Василиса Прекрасная, в другой находится Змей Горыныч, а третья темница – пустая. Учти, что все надписи на дверях темниц неверные.
Бросил Иван клубок на землю. Покатился клубок, а Иван – за ним. Долго ли, коротко ли, он дошел до Кощея Бессмертного. Потребовал Иван у него Василису Прекрасную.
Повел Кощей Ивана в подземелье. Показал там три темницы, на дверях которых написано: темница 1 – «Здесь Василиса Прекрасная»;
Темница 2 – «Темница 3 не пустая»;
Темница 3 – «Здесь Иван Горыныч».
- Отпущу, Иван, с тобой Василису Прекрасную, если угадаешь, в какой она темнице. Покажешь на дверь, за которой Змей Горыныч,- быть тебе им растерзанным. Покажешь на пустую темницу – быть тебе в ней узником до конца своих дней.
Задумался Иван… Ребята, посоветуйте Ивану, на какую дверь ему показать.
(Ответ. Василиса Прекрасная во 2 темнице.
Надпись на двери темницы 2 неверная, т.е. темница 3 пустая. Значит, 1 и 2 темницы не пустые. Надпись на двери 1 темницы тоже неверная. Значит, там Змей Горыныч. Тогда во второй темнице Василиса Прекрасная.)
Задача. Восьмое путешествие Синбада.
Синбад- Мореход попал на остров. На нем живут только правдолюбы (они всегда говорят правду) и лгуны (они всегда лгут). Синбада
сопровождал проводник – житель этого острова. Вскоре они увидели еще одного жителя острова. Синбад послал проводника узнать, кто этот житель острова – правдолюб или лгун. Проводник вернулся и сказал, что тот говорит, что лгун. Кто был проводник – правдолюб или лгун?
(Ответ: Проводник оказался лгуном. Если бы житель острова оказался правдолюбом, то он об этом сообщил бы проводнику. Если же житель острова лгун, то он по-прежнему сообщил бы, что он правдолюб. Таким образом, ожидаемый ответ: правдолюб. Проводник же Синбаду сообщил о жителе острова, что он лгун. Значит проводник – лгун.)
Задача. Как лиса и волк рыбу делили.
Обманным путем лиса и волк раздобыли целую кучу рыбы. Лиса рисковала своей шкурой. Да и волку крепко досталось – бока болят от побоев.
Лиса говорит:
- Давай, волк, разделим рыбу поровну.
- Давай! Слаб я в математике, дели ты, лиса.
Бросила лиса волку 1 рыбу, а себе 2:
- Вот тебе, волк, одна рыбка, а мне две…
- Не слишком ли мало?!
- Слушай дальше. Тебе 3 рыбки…
- Это можно!
- А мне 4, тебе 5, а мне 6, тебе 7…
И так далее.
Разделила лиса всю рыбу, каждый раз поочередно увеличивая количество рыбок на одну. Последний раз лиса бросила себе 20 штук и на этом рыба кончилась.
Доволен волк, полагая, что он получил рыбы столько же, сколько и лиса.
Как по-вашему, ребята, кто больше получил рыбок: лиса или волк и на сколько?
(Ответ: Лиса получила на 10 рыбок больше.
Составим два ряда чисел:
Волк: 1 3 5 7 9 11 13 15 17 19
Лиса: 2 4 6 8 10 12 14 16 18 20
Каждый раз лиса себе бросала на 1 рыбку больше. )
Задача. Два жадных медвежонка.
Два медвежонка нашли головку сыра. Они долго спорили как её поделить, но никто не хотел уступать. Мимо пробегала лиса. Узнав, о чем спор, она предложила помочь.
Разломив головку сыра на две части так, чтобы одна из них была ровно полкилограмма, а другая меньше, она спросила, облизнувшись:
- Куски равны?
- Нет! – закричали жадные медвежата.
Тогда лиса откусила от большей части, но столько, что этот кусок стал меньше, чем другая часть, и повторила вопрос. И на этот раз медвежата сообщили, что получились неравные куски. Затем лиса ещё 9 раз пыталась сделать части равными, поочередно откусывая от них одинаковое количество сыра. В результате остались маленькие кусочки, причем один из них оказался на 20 г больше другого. После этого лиса заявила, что медвежатам трудно угодить. Она отправила оба кусочка в рот и, вильнув хвостом. Скрылась в кустах.
Какова была масса головки сыра?
(Ответ: Масса головки сыра 980 г.
Лиса всего откусила 10 раз – от каждой части поочередно по 5 раз. Значит, от каждой части откушено одинаковое количество сыра, т.е. вторая часть содержит сыра на 20г меньше, чем первая. Первоначальная масса сыра была 500 + (500 – 20) = 980 г.
Задача. Старик Хоттабыч.
Возраст старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее:
Если первую и последнюю цифры зачеркнуть, то получится двузначное число, которое при сумме цифр, равной 13, является наибольшим;
Первая цифра больше последней в 4 раза.
Сколько лет старику Хоттабычу?
(Ответ: Старику Хоттабычу 8942 года. Наибольшим двузначным числом с суммой цифр, равной 13, является 94. Пусть последняя цифра 1. Тогда первая цифра равна 4. Но такая цифра в числе есть, а ведь цифры в числе должны быть разными. Пусть последняя цифра 2, тогда первая 8. Все цифры различны. Итак, получилось число 8942.)
Задача. Красная Шапочка идет к бабушке.
Красная Шапочка несла бабушке 14 пирожков: с мясом, грибами и капустой. Пирожков с капустой наибольшее количество. Причем их вдвое больше, чем пирожков с мясом. А пирожков с мясом меньше, чем пирожков с грибами. Сколько пирожков с грибами?
(Ответ: Красная Шапочка несла 5 пирожков с грибами.
Пусть пирожков с мясом 2, тогда с капустой 2× 2= 4. Значит, с грибами 14 – (2 +4) = 8. Но в этом случае пирожков с капустой не наибольшее количество.
Пусть пирожков с мясом 3, тогда с капустой 3 × 2=6. Значит, с грибами 14 – 3 – 6= 5. Этот результат соответствует условию задачи.
Задача. Домик кума Тыквы.
Кум Тыква с самого детства мечтал о том, что у него будет когда-нибудь собственный домик. Он с 15 лет каждый год покупал по одному кирпичу для будущей постройки. Через некоторое время мастер Виноградинка посчитал кирпичи. Их оказалось у кума Тыквы 18. Мастер Виноградинка сказал, что этих кирпичей на домик не хватит. Кум Тыква думал-думал и в конце концов решил работать побольше, а есть поменьше. Так он и сделал. Теперь ему удавалось покупать по 4 кирпича в год. Когда всех кирпичей оказалось 118 штук, кум Тыква начал строить домик. Через два года кум тыква поселился в своем тесном домике. Сколько лет тогда было куму Тыкве?
(Ответ: Когда Кум тыква окончил строить домик, ему было 60 лет. Решение ясно из числового выражения: 15+18+(118-18): 4+2=60.
Задача. Пончик на фабрике Жадинга.
Во время путешествия Незнайки на Луну его друг Пончик был вынужден устроиться на фабрику мистера Жадинга на срок не более чем 10 дней. Условия следующие: за день работы Пончику начисляется 3 фертинга, а за прогул в течение дня – штраф 4 фертинга. Работа оказалась тяжелой: целый день приходилось носить огромные мешки. Так что каждый день, следующий за днем работы Пончик не мог не только выйти на работу, но и даже разогнуться.
Спустя некоторое время мистер Жадинг вызвал Пончика в свой кабинет:
- Работы больше нет, так что мы не нуждаемся в ваших услугах. Получите расчет у кассира. От всей души желаю дальнейших успехов!
Кассир сообщил:
- Вы заработали некоторую сумму. Но её как раз хватило на покрытие
штрафов из-за прогулов. Сколько дней работал Пончик?
(Ответ: 4 дня. В 1 день Пончик заработал 3 фертинга, во второй день он не вышел на работу – штраф 4 фертинга. Долг Пончика составил 1 фертинг. Через 3 пары дней долг Пончика составил 3 фертинга. На 7-й день Пончик заработал 3 фертинга, чем покрыл свой долг. Таким образом, Пончик работал всего 4 дня.)
Поросята Ниф-Ниф и Нуф-Нуф бежали от Волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика Наф-Нафа 6 минут. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?
(Ответ: Волку надо бежать до домика Наф-Нафа 4 + 6 : 2=7(мин), а поросятам 6 мин. 6 7. Значит, поросята успеют добежать до домика Наф-Нафа.)
Музыкант Гусля живёт выше поэта Цветика, но ниже художника Тюбика, а Незнайка живёт ниже поэта Цветика. На каком этаже четырёхэтажного дома живёт каждый из них? (Ответ: Гусля – 3 этаж, Цветик – 2 этаж, Незнайка – 1 этаж, Тюбик – 4 эт.)
Илья Муромец, Добрыня Никитич, Алеша Попович вступили в бой с несколькими великанами. Каждый великан получил по 3 удара богатырскими палицами, в результате чего все великаны обратились в бегство. Больше всего ударов нанес Илья Муромец, меньше всего Алеша Попович – 3. Сколько всего было великанов?
(Ответ: 5 великанов.
Между числами 3 и 7 находятся числа 4, 5,6. Число всех ударов должно делиться на 3. Значит, Добрыня Никитич нанес 5 ударов. Всех ударов палицей по великанам было 3+7+5=15.
Следовательно, всего было 15 : 3 = 5 (великанов).
Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. Они живут на второй планете. Далее передача ухудшилась из-за помех, но было принято еще два сообщения, которые как установили ученые, оба неверные:
1) А – не третья от звезды планета; 2) Б – вторая планета.
На какой планете (А,Б или В) живут инопланетяне?
(Ответ: инопланетяне живут на планете В. А – не третья от звезды планета- это сообщение неверно. Значит, А – третья планета.
Б – вторая планета – тоже неверно. Значит, Б – первая планета.
Остается принять, что В – вторая планета.).
Логические задачи.
Задачи 1 класс.
В магазине было 3 холодильника. Продали меньше, чем осталось. Сколько холодильников продали?
(Ответ: Продали 1 холодильник, осталось – 2.)
Брат и сестра пришли в школу одновременно. Брат шёл быстрее. Кто из них вышел раньше? ( Ответ: раньше вышел брат.)
Аркадий – сын Романа, Роман – сын Василия. Кем приходится Аркадий Василию, а Василий Аркадию?
(Ответ : Василий – дед, а Аркадий – внук.)
Росли три вербы, на каждой вербе – по 2 ветки. На каждой ветке – по 2 груши. Сколько всего груш? (Ответ: На вербе груши не растут )
Летела стая уток. Охотник выстрелил и одну убил. Сколько уток осталось?
(Ответ: так как все утки улетели, то не осталось ни одной)
На верёвку завязали 5 узлов. На сколько частей эти узлы разделили верёвку? (Ответ: на 6частей.)
Рыбак поймал окуня, ерша и щуку. Щуку он поймал раньше, чем окуня, а ерша позже, чем щуку. Какая рыба поймана раньше всех? Можно ли сказать, какая рыба поймана позже всех?
(Ответ: Раньше всех поймали щуку. При ответе на второй вопрос возможны два варианта: 1. Щука, ёрш, окунь. 2. Щука, окунь, ёрш.)
Что тяжелее 1 кг ваты или 1 кг железа.
(Ответ: 1 кг ваты = 1 кг железа).
В банке столько же воды, сколько в кастрюле, а в кастрюле столько же воды, сколько в миске. Где больше воды: в банке или миске?
(Ответ: одинаково).
Оля выше Кати. Кто из девочек ниже? (Ответ: Оля выше, Катя ниже).
По направлению к городу ехало 3 машины, а навстречу им ехало 5 автобусов. Сколько машин ехало в город? ( Ответ: 3 машины.)
Марина и Оля сёстры. Марина сказала, что у неё 2 брата, а Оля сказала, что у неё тоже два брата. Сколько детей в семье?
(Ответ: 4 детей.)
Масса петуха, стоящего на двух ногах 4кг. Какова будет масса петуха, если он встанет на одну ногу? (Ответ: такая же.)
Масса дрессированной собаки, когда она стоит на задних лапах 3 кг. Какова будет её масса, если она встанет на ноги?
(Ответ: такая же.)
Мама, папа и я сидели на скамейке. В каком порядке мы сидели на скамейке, если известно, что:
а) я сидела справа от папы, а мама слева от меня;
(Ответ: папа, мама, я.)
б) папа сидел слева от меня и справа от мамы;
(Ответ: мама, папа, я.)
в) мама сидела справа от меня, а папа справа от мамы
(Ответ: я, мама, папа.).
Иван Петрович – отец Нины Ивановны, а Толя – сын Нины Ивановны. Кем Толя приходится Ивану Петровичу? ( Ответ: внуком.)
Коля ростом выше Васи, но ниже Серёжи. Кто выше Вася или Серёжа?
(Ответ: Серёжа выше Васи.)
Миша выше Пети, а Катя ниже Миши. Кто выше – Катя или Петя?
(Ответ: Нельзя ответить на вопрос задачи.)
Сколько лет моему дедушке, если через 15 лет мы будем отмечать его семидесятилетие? (Ответ: 55 лет.)
Саше, Маше, Тане и Ване купили по воздушному шарику. Машин шарик не самый маленький, но меньше, чем у Саши и Вани. Сашин шарик не меньше, чем Ванин. У кого какой шарик?
( Ответ : Самый маленький шарик у Тани, средний шарик у Маши, большие шарики – у Саши и у Вани.)
Ира и Лена одинакового роста. Лена ростом выше Оли, а Таня выше Иры. Кто выше: Таня или Оля? (Ответ : Таня выше Оли.)
Катя и Лена собрали по одному стакану ягод. Катя пересыпала свои ягоды в маленькую банку, а Лена в большую корзину. Где ягод больше: в большой корзине или в маленькой баночке? (Ответ: ягод было одинаковое количество, девочки набрали по одному стакану.)
В квартирах № 1,2,3 жили три котенка: белый, черный, рыжий. В квартирах № 1 и 2 жил не черный котенок. Белый котенок жил не в квартире № 1. В какой квартире жил каждый котенок?
(Ответ: черный котенок жил в квартире № 3, белый – в квартире № 2, а рыжий – в квартире № 1.)
Три товарища Алеша, Коля и Саша, сели на скамейку в один ряд. Сколькими способами они могут это сделать? (Ответ: 6 способов. А-Алеша, К-Коля, С-Саша. АКС, АСК, КАС, КСА, САК,СКА.)
31
Меня зовут Толей. У моей сестры только один брат. Как зовут брата моей сестры? (Ответ: Толя.)
Термометр показывает три градуса мороза. Сколько градусов покажут два таких термометра? (Ответ: три градуса.)
Петя и Миша имеют фамилии Белов и Чернов. Какую фамилию имеет каждый из ребят, если Петя на 2 года старше Белова?
( Ответ: Петя Чернов, Миша Белов.)
Четыре человека обменялись рукопожатиями. Сколько было рукопожатий? (Ответ: 6 рукопожатий.)
У мальчика в коробке было 7 мух. На две мухи он поймал двух рыбок. Сколько рыбок он поймает на остальных мух?
(Ответ: Задача не имеет решения, так как не всегда можно на 1 муху поймать рыбу.)
Год назад Ире было 5 лет. Сколько ей будет через три года?
(Ответ: 5 + 1 + 3 = 9 лет.)
Ребята прыгали в длину. Дима прыгнул дальше Пети, а Сергей ближе Пети. Андрей прыгнул ближе Сергея, но дальше Юры. Коля прыгнул дальше Димы, а Борис так же, как и Петя. Кто прыгнул дальше: Дима или Серёжа? Петя или Андрей? Кто прыгнул ближе: Юра или Борис? Борис или Дима?
(Ответ :
____________________________________________________________
Ю А С Б П Д К
Дима прыгнул дальше, чем Серёжа.
Петя прыгнул дальше, чем Андрей.
Ближе прыгнул Юра, чем Борис.
Борис прыгнул ближе, Дима дальше.)
Куда войдёт больше воды: в трёхлитровый чайник или трёхлитровый самовар? (Ответ: воды войдёт поровну, так как чайник и самовар, одинаковые по объёму.)
Ваня прошёл 20 шагов, а Саша – 19 шагов. Кто из них прошёл большее расстояние? (На вопрос ответить невозможно, так как у мальчиков может быть разная длина шага.)
На грядке сидели 6 воробьёв. К ним прилетели ещё 3 воробья. Кот подкрался и схватил одного воробья. Сколько воробьёв осталось на грядке? (Ответ: на грядке не останется ни одного воробья, потому что все улетят.)
Список литературы.
1. Узорова.О.В. Контрольные и олимпиадные работы по математике. – М.: ООО «Издательство Астрель», 2006. – 127с.
3. Математика. 1-4 классы: упражнения для устного счета/ сост. М.В.Головач, Ю.К.Бондаренко.- Волгоград: Учитель, 2008.- 266с.
4. Петерсон.Л.Г и др. Самостоятельные и контрольные работы по математике в начальной школе. Выпуск 4. – М.: Баласс, 2008. – 96с.
5. Петерсон.Л.Г. Самостоятельные и контрольные работы по математике в начальной школе. Выпуск 1. – М.: Баласс, 2008. – 80с.
6. Петерсон.Л.Г. Самостоятельные и контрольные работы по математике в начальной школе. Выпуск 3. – М.: Баласс, 2007. – 96с.
7. Петерсон.Л.Г. Самостоятельные и контрольные работы по математике в начальной школе. Выпуск 2. – М.: Баласс, 2009. – 96с.
8. Математика. 1 класс: Поурочные планы: Поурочные планы/ Авт. – сост. Т.В.Бут. – Волгоград: Учитель, 2003. – 384с.
11. Максимова.Т.В., Целоусова Т.Ю. Поурочные разработки по математике. 3класс. М.: «ВАКО», 2004. – 400с.
13.Русанов В.Н. Математические олимпиады младших школьников: Кн. Для учителя: Из опыта работы.- М.: Просвещение, 1990.-77с.
14. С.И.Волкова, Н.Н.Столярова. Задания на развитие логического мышления.// Начальная школа, 1990, № 7. – с. 38 – 41.
15.С.И.Волкова, Н.Н. Столярова. Развитие познавательных способностей учащихся на уроках математики.// Начальная школа, 2004, №8. – с.29 – 36.
16. Л.Ф.Тихомирова, А.В.Басов. Развитие логического мышления детей.- Ярославль: ТОО «Гринго», 1995. – 240с.
17. И.В.Сереброва. Развитие внимания и логического мышления на занятиях по математике.// Начальная школа, 1995, №6. –с. 51-53.
18. А.Э.Симановский. Развитие творческого мышления детей. – Ярославль: «Гринго», 1996. – 192с.
9

 Получите свидетельство
Получите свидетельство Вход
Вход












 Сборник заданий на развитие мышления младших школьников на уроках математики (82.43 KB)
Сборник заданий на развитие мышления младших школьников на уроках математики (82.43 KB)
 0
0 5007
5007 320
320 Нравится
0
Нравится
0


