Урок
Тема: «Ромб, квадрат. Свойства ромба, квадрата»
Тип урока: изучение нового материала
Цель урока: формирование представления о ромбе и квадрате.
8 класс
Задачи:
Обучающие: Ввести понятия ромба и квадрата как частных видов параллелограмма. Рассмотреть свойства ромба и квадрата и показать их применение в процессе решения задач
Воспитательные: воспитание интереса к изучению математики, ответственности, самостоятельности.
Развивающие: развитие умений применять полученные теоретические знания при выполнении практических заданий.
Оборудование: мультимедийный проектор, компьютер, интерактивная доска, линейка, цветные мелки.
Планируемые результаты:
Предметные: применяют свойства ромба и квадрата при решении задач.
Личностные: Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают оценку результатов своей учебной деятельности.
Метапредметные:
Р – определяют цель учебной деятельности, осуществляют поиск средств её осуществления.
П – делают предположения об информации, которая нужна для решения учебной задачи.
К – умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами.
Структура урока:
| 1. | Организационный момент | 1 мин |
| 2. | Проверка Д\З | 3 мин |
| 3. | Повторение опорного теоретического материала через устный счет | 8 мин |
| 4. | Формулирование темы и цели урока | 2 мин |
| 5. | Ознакомление с новым материалом | 15 мин |
| 6. | Физкультминутка | 2 мин |
| 7. | Перенос приобретенных знаний и их первичное применение в новых условиях с целью формирования умений | 5 мин |
| 8. | Рефлексия | 2 мин |
| 9. | Постановка Д/З | 2 мин |
Ход урока
| Учитель | Ученики | УУД |
| Организационный момент |
| |
| Приветствую учащихся. Сажаю их на места.
| Приветствуют учителя. |
|
| Проверка Д/З |
| |
| Какие вопросы по домашнему заданию?
| Спрашивают.
| К: оформлять свои мысли в устной речи |
| Повторение опорного теоретического материала через устный счет |
| |
| К Найдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.
Решение. Так как ABCD – прямоугольник, то AD | | ____ и поэтому Но с основанием ___. Значит, АВ = ___ = ___ см. 2) AD = AE + ED = ___ + ___ = ___; PABCD = 2*(____ + ____) = =2*(___ см + ___см) = 2*___ см = ___см. Ответ: PABCD =___см.
Карточка №2. В Решение. В прямоугольном треугольнике ABD BD = 2*__=__см. Так как в прямоугольнике диагонали ______, то АС = ___=___см. Ответ: АС= ___ см.
- Какая фигура называется прямоугольником? - Каким свойствами обладает прямоугольник? - Сформулируйте признак прямоугольника? Решите задачи по готовым чертежам: (слайд 1) 1) ABCD - прямоугольник. Найти: ∠ABF. (слайд 2) 2) АСЕК - прямоугольник, ВС = 5 см. Найти: PBDFM.
(слайд 3) 3) ABCD - прямоугольник. Найти: ∠AOB, ∠BOC.
(слайд 4) - Является ли параллелограммом четырёхугольник АВСD?
- Почему? -Такой четырёхугольник является ещё одним частным случаем параллелограмма и называется ромбом. - Какими свойствами и признаками обладает данная фигура? - Кто догадался, чем мы будем заниматься на уроке?
|
решают
отвечают с места
200
10*4 = 40 см
∠BOC = 1200
∠AOB = 600 | П: уметь ориентироваться в своей системе знаний К: уметь слушать и понимать речь других, оформлять мысли в устной речи Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение |
| Формулирование темы урока, постановка его цели и задач |
| |
| - Кто сформулирует тему и цель сегодняшнего урока? (слайд 5) | Формулируют, записывают в тетрадях число, кл/р, тема урока |
|
| 5. Ознакомление с новым материалом |
| |
| - Давайте будем разбираться с данной фигурой. - Сформулируйте определение ромба. (слайд 6) Определение: Ромбом называется параллелограмм, у которого все стороны равны. - Сформулируйте свойства параллелограмма. Свойства: 1. В параллелограмме противоположные стороны равны. 2. В параллелограмме противоположные углы равны. 3. Диагонали параллелограмма точкой пересечения делятся пополам. 4. Сумма односторонних углов параллелограмма равна 1800.
- Какими свойствами обладает ромб? Почему? Сформулируйте их. Теми же, что и параллелограмм. Т.к. ромб является параллелограммом.
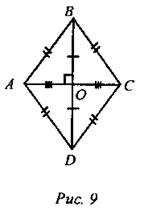
Свойства: 1. В ромбе противоположные стороны равны. 2. В ромбе противоположные углы равны. 3. Диагонали ромба точкой пересечения делятся пополам. 4. Сумма односторонних углов ромба равна 1800. - Выясните, каким еще свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. Постройте ромб АВСD. Проведите диагонали АС и ВD.
-Сравните взаимное расположение диагоналей ромба? Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Дано: ABCD-ромб Доказать: АС ( Доказательство: AB = AD (по определению ромба), АО = ОС, ВО = DО (т.к. ромб – параллелограмм), Поэтому АС (Равенство остальных углов ромба доказываются аналогично). (Г/Ф) - Сформулируйте утверждение, обратное особому свойству ромба, и выясните его справедливость. Теорема – признак: Если в параллелограмме диагонали взаимно перпендикулярны, то параллелограмм является ромбом. Дано: параллелограмм ABCD, АСBD. Доказать: ABCD – ромб.
Доказательство: 1. АВС – равнобедренный (по признаку равнобедренного треугольника), т.к. ВО –высота и медиана АВС, ( ВО=ОD (по св-ву диагоналей параллелограмма)) т.е. АСВD. Следовательно, АВ=ВС (по следствию из определения равнобедренного треугольника).
2. АВ=ВС=СD=АD, т.к. в параллелограмме АВСD АВ=СD, ВС=АD (по свойству параллелограмма)АВ=ВС (из п.1) АВСD – ромб (по определению). Свойства: 1. В ромбе диагонали взаимно перпендикулярны. 2. В ромбе углы делятся диагональю пополам. Признаки: 1. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом. 2. Если в параллелограмме углы делятся диагональю пополам, то этот параллелограмм является ромбом.
-Является ли прямоугольником четырёхугольник АВСD? - Почему? (слайд 7) В А D - Такой четырёхугольник является ещё частным случаем прямоугольника, а значит и параллелограмма, и ромба - называется квадратом. Определение. Квадратом называется прямоугольник, у которого все стороны равны. - Значит квадрат обладает всеми свойствами прямоугольника и ромба. Квадрат обладает всеми свойствами прямоугольника и квадрата: (слайд 7) 1) Все углы квадрата прямые 2) Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам - Сформулируйте признаки квадрата
| отвечают с места по одному
записывают
(Работа в группах с последующим обсуждением свойства диагоналей ромба.)
формулируют записывают
рассуждают записывают
| П: уметь добывать новые знания. Р: уметь работать по коллективно составленному плану, проговаривать последовательность действий на уроке. К: уметь слушать и понимать других, оформлять свои мысли в устной и письменной речи |
| 5. Физкультминутка |
| |
| Я скажу несколько математических предложений. Если предложение верное, то вы сидите, если оно ложное, то вы встаёте, и кто-то из вас объясняет, почему ложное. Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. (+) В параллелограмме противоположные стороны и противоположные углы равны. (+) В параллелограмме диагонали равны. (-) В параллелограмме диагонали точкой пересечения делятся пополам. (+) Диагонали прямоугольника точкой пересечения делятся пополам. (+) Сумма углов выпуклого четырёхугольника равна 180◦. (-) В прямоугольнике противоположные стороны равны. (+) Ромб обладает всеми свойствами прямоугольника. (-) Квадрат не обладает всеми свойствами ромба. (-) Квадрат обладает всеми свойствами параллелограмма, прямоугольника, ромба. (+)
|
|
|
| 6. Перенос приобретенных знаний и их первичное применение в новых условиях с целью формирования умений |
| |
| № 406 Дано: ABCD - ромб, ∠B = 60°, АС = 10,5 см. Найти: РАВCD.
Решение: ∠B = 60°, АВ = ВС (так как АВ и ВС - стороны ромба), тогда ∠BAС = ∠BCA= 60°, то есть ∆АВС - равносторонний и АВ = АС = 10,5 см. У ромба все стороны равны, поэтому PABCD = 4 ∙ АВ = 4 ∙ 10,5 = 42 (см). Ответ: 42 см. № 407 Решение: ∠ABC = 45°. BD - диагональ и биссектриса ∠ABC. ∠ABD = 45° : 2 = 22°30' Из ∆ABO (∠O = 90°, так как диагонали ромба перпендикулярны): ∠OAB = 90° - 22°30' = 67°30' Ответ: 22°30’, 67°30'
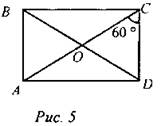
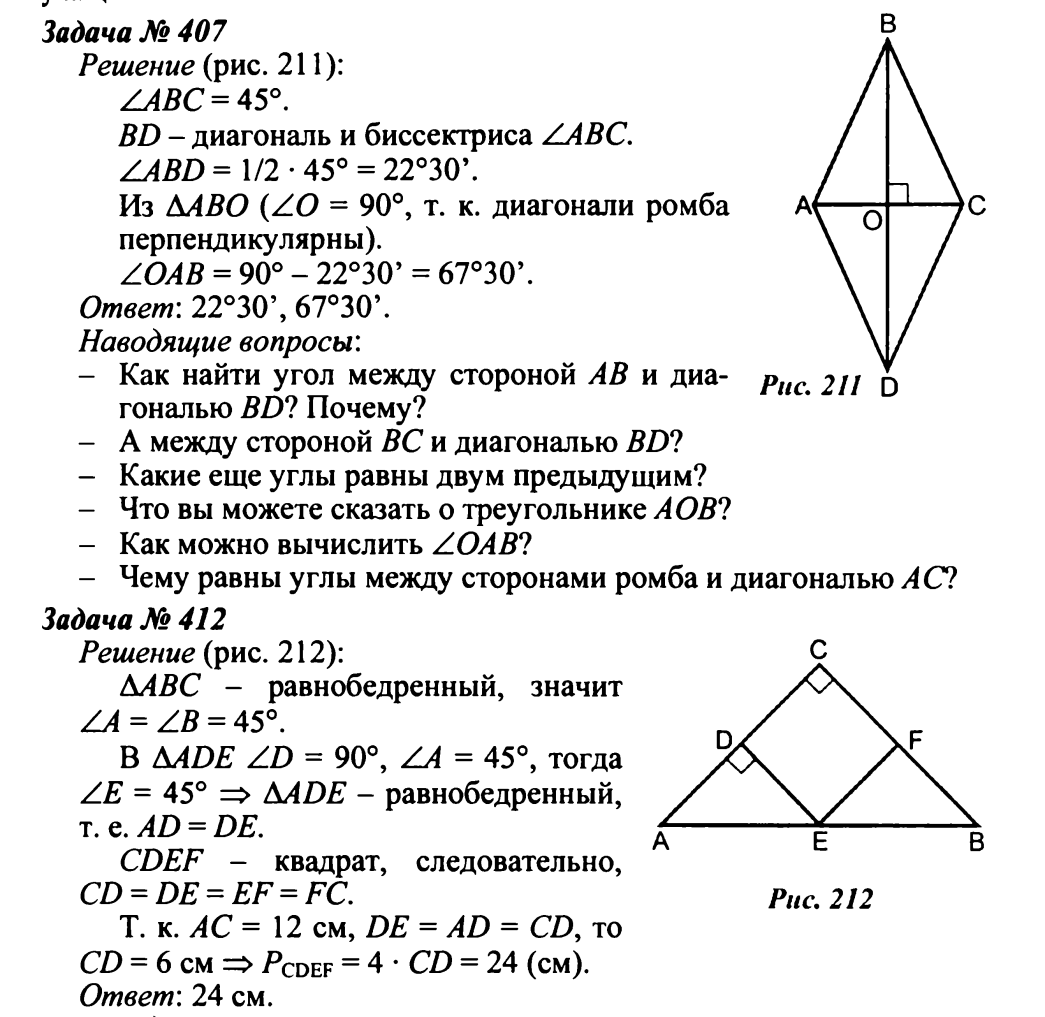
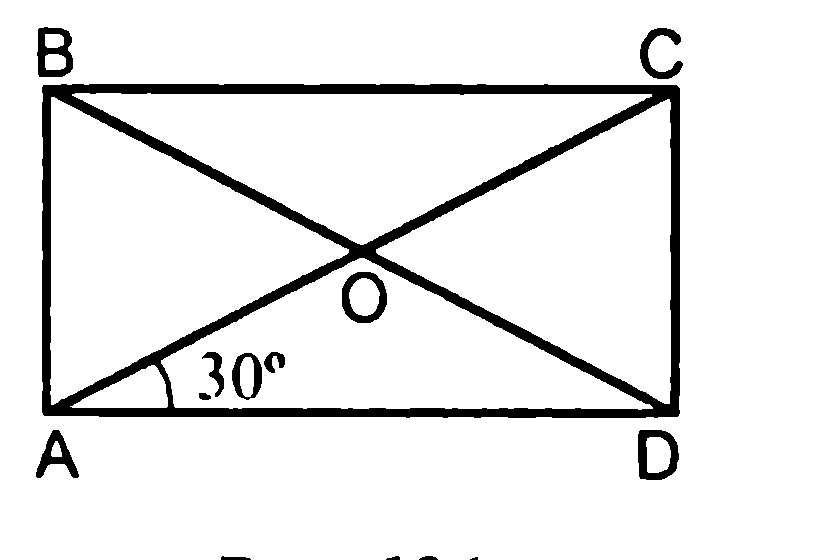
№ 403 у доски. Дано: ABCD – прямоугольник, AC ∩ BD = O, CAD = 300, AC = 12 см. Найти: P AOB
|
один ученик у доски, остальные в тетрадях.
один ученик у доски, остальные в тетрадях.
| П: делают предположения об информации, которая нужна для решения учебной задачи. К: умеют критично относиться к своему мнению |
| 8. Рефлексия |
| |
| Какое задание вам больше всего понравилось? Какие задания вызвали затруднения? С каким настроением уходим с урока? | Поднимают руки. |
|
| 9. Постановка Д/З |
| |
| п. 47, №405, 402 | Слушают, записывают. |
|
Карточка №1.
Найдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.
Р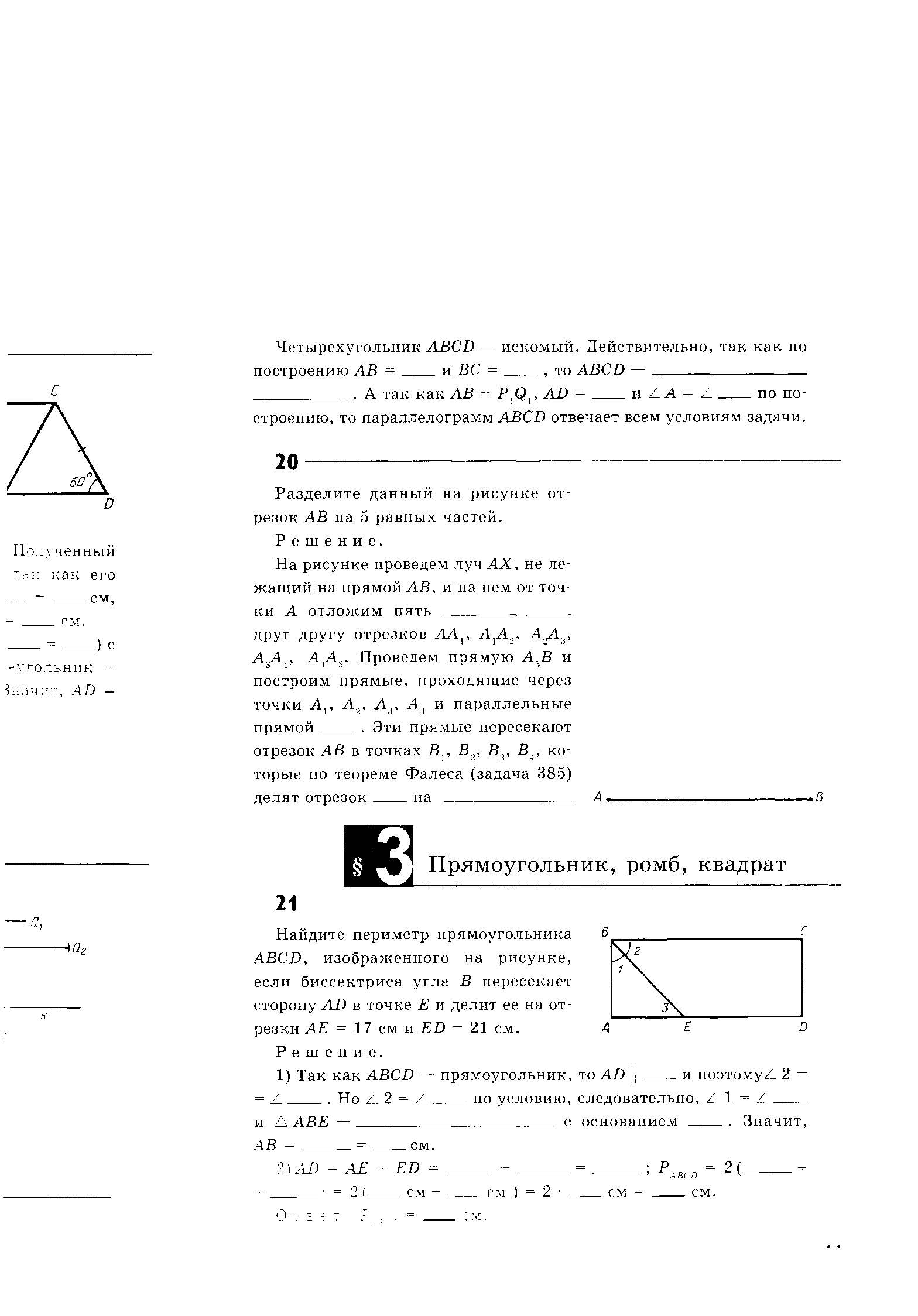 ешение.
ешение.
1) Так как ABCD – прямоугольник, то AD | | ____ и поэтому 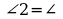 ___.
___.
Но 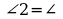 ___ по условию, следовательно,
___ по условию, следовательно, 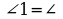 __ и ▲ABE - ____________ с основанием ___. Значит, АВ = ___ = ___ см.
__ и ▲ABE - ____________ с основанием ___. Значит, АВ = ___ = ___ см.
2) AD = AE + ED = ___ + ___ = ___; PABCD = 2*(____ + ____) =
= 2*(___ см + ___см) = 2*___ см = ___см.
Ответ: PABCD =___см.
Карточка №2.
В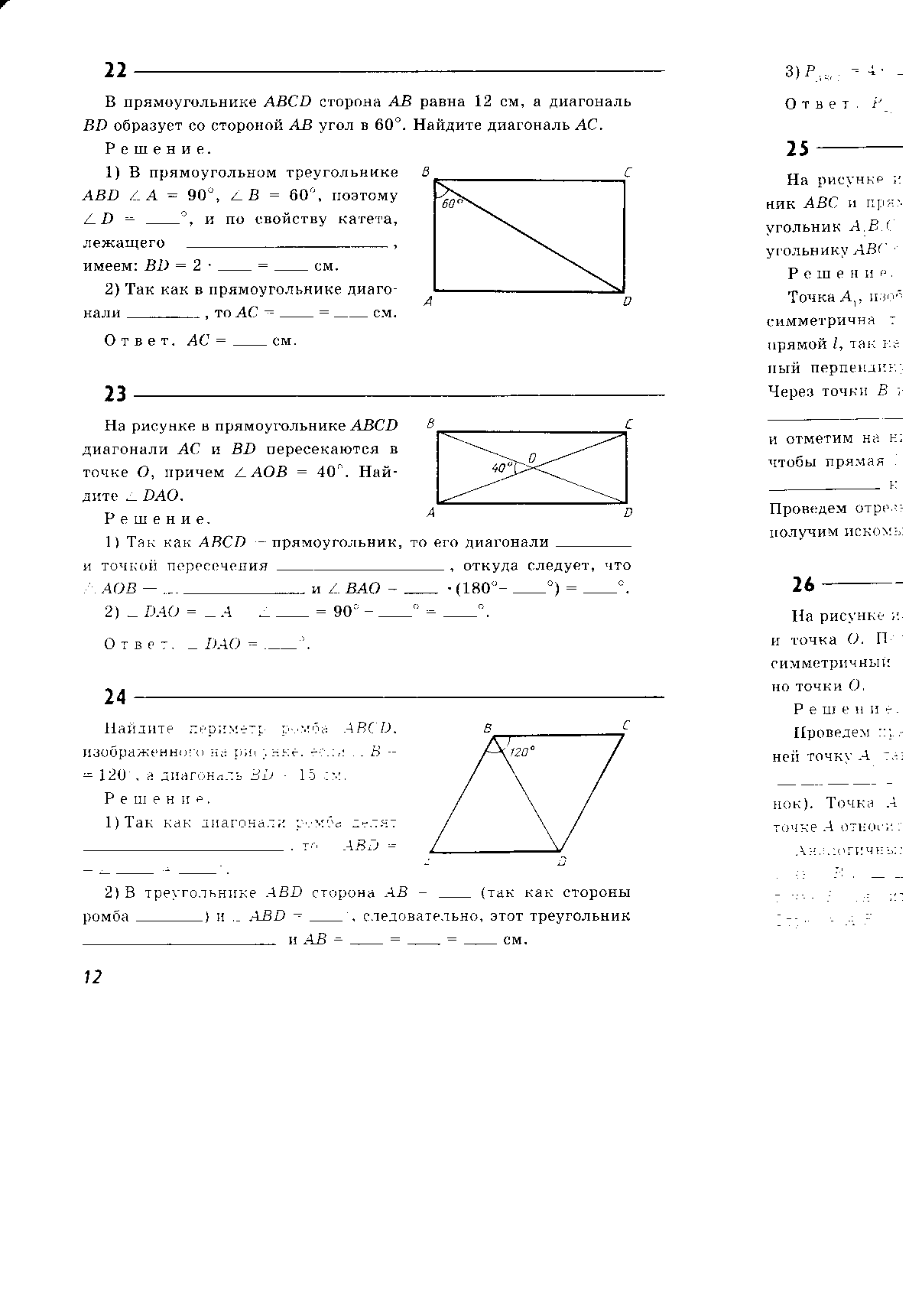 прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
Решение.
1) В прямоугольном треугольнике ABD 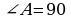 ◦,
◦, 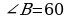 ◦, поэтому
◦, поэтому 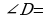 ___◦, и по свойству катета, лежащего _______________, имеем:
___◦, и по свойству катета, лежащего _______________, имеем:
BD = 2*__=__см.
2) Так как в прямоугольнике диагонали ______, то
АС = ___=___см.
Ответ: АС= ___ см.
Карточка №1.
Найдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.
Р ешение.
ешение.
1) Так как ABCD – прямоугольник, то AD | | ____ и поэтому 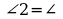 ___.
___.
Но 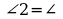 ___ по условию, следовательно,
___ по условию, следовательно, 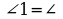 __ и ▲ABE - ____________
__ и ▲ABE - ____________
с основанием ___. Значит, АВ = ___ = ___ см.
2) AD = AE + ED = ___ + ___ = ___;
PABCD = 2*(____ + ____) = 2*(___ см + ___см) = 2*___ см = ___см.
Ответ: PABCD =___см.
Карточка №2.
В прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60◦. Найдите диагональ АС.
Решение.
1) В прямоугольном треугольнике ABD 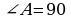 ◦,
◦, 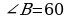 ◦, поэтому
◦, поэтому 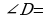 ___◦, и по свойству катета, лежащего _______________, имеем:
___◦, и по свойству катета, лежащего _______________, имеем:
BD = 2*__=__см.
2) Так как в прямоугольнике диагонали ______, то
АС = ___=___см.
Ответ: АС= ___ см.
11

 Получите свидетельство
Получите свидетельство Вход
Вход


 арточка №1.
арточка №1.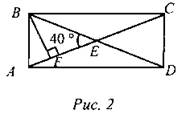
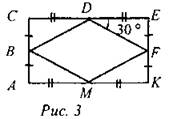


 BD
BD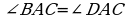
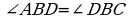 ,
, 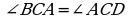 ,
, 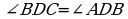 )
)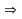 ▲BAD равнобедренный.
▲BAD равнобедренный. С
С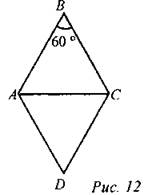









 «Ромб, квадрат. Свойства ромба, квадрата» (546.09 KB)
«Ромб, квадрат. Свойства ромба, квадрата» (546.09 KB)
 0
0 76
76 1
1 Нравится
0
Нравится
0



