Решение задач с помощью систем уравнений

Тема: «Решение задач с помощью систем уравнений»

Цель урока: Создать условия для формирования умения решать задачи с помощью систем уравнений с двумя неизвестными.

Задачи:

• образовательная: вывести алгоритм решения задач с помощью систем уравнений с двумя неизвестными;

• развивающая: развивать потребность в нахождении рациональных способов решения; содействовать развитию способности рассуждать, ставить вопросы и отвечать на них;

• воспитательная: способствовать развитию любознательности и творческой активности обучающихся.

Планируемые результаты:

Предметные результаты:

• строить модель условия задачи (в виде таблицы, схемы или рисунка), в которой даны значения двух из трех взаимосвязанных величин, с целью поиска решения задачи;

• осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;

• составлять план решения задачи;

• интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

• решать несложные логические задачи методом рассуждений.

Метапредметные результаты:

• самостоятельно определять цели, задавать параметры и критерии, по которым можно определить, что цель достигнута;

• оценивать возможные последствия достижения поставленной цели в деятельности, собственной жизни и жизни окружающих людей, основываясь на соображениях этики и морали;

• ставить и формулировать собственные задачи в образовательной деятельности и жизненных ситуациях;

• оценивать ресурсы, в том числе время и другие нематериальные ресурсы, необходимые для достижения поставленной цели;

• выбирать путь достижения цели, планировать решение поставленных задач, оптимизируя материальные и нематериальные затраты;

Личностные результаты :

• готовность и способность к отстаиванию личного достоинства, собственного мнения, готовность и способность вырабатывать собственную позицию;

• готовность обучающихся к конструктивному участию в принятии решений, затрагивающих их права и интересы, в том числе в различных формах общественной самоорганизации, самоуправления, общественно значимой деятельности.

Ход урока.

-Добрый день ребята я приветствую вас и наших уважаемых гостей от вашего имени также.

1.Организационный момент.

-Открываем тетради, записываем число, классная работа.

-Среднеазиатский ученый Абу-р-Райхан ал-Бируни сказал

«Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит».

-Вот и мы с вами будем стремиться к знаниям.(Слайд №1)

2.Сообщение темы.

-Т.к. урок у нас сегодня не совсем обычный, начнем с интеллектуальной разминки.

-Я предлагаю вам разгадать ребусы.(Слайд №2)

-А сейчас ребята вам не составит труда сформулировать тему урока.(Слайд№3)

3.Постановка целей урока.

-Давайте определимся с целями урока

-Научится решать задачи.

-Составлять таблицу.

-Составлять систему уравнений.

-Выбирать более удобный способ решения.

4.Актуализация знаний.

Решение задач с помощью систем уравнений

-Какие математические понятия нужны нам на уроке?

-Что называется решением системы?

-Что значит решить систему?

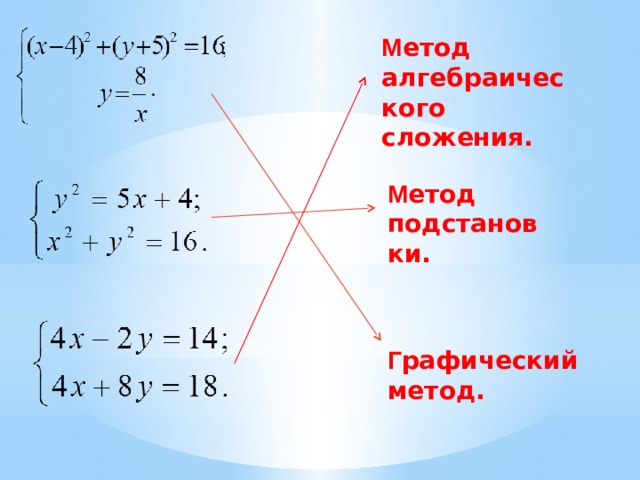
-Перечислите методы решения систем уравнений.

5.Решение проблемной задачи.

-А теперь применим наши знания на практике.

- Является ли пара чисел (0;1) решением системы уравнений (Слайд №4)

- Определить для каждой системы уравнений рациональный метод решения(Слайд №5)(На доске)Правильный ответ (Слайд №6)

-Молодцы .А теперь усложняем задание.

-Рассмотрим задачу, одну из сложных задач на экзамене.(Слайд №7)

-О чем говорится в задачи?

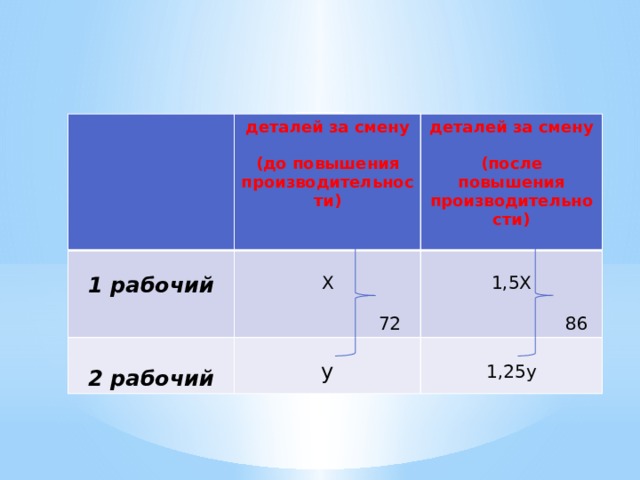
-Сколько было рабочих?

-Составим таблицу(На доске )(Слайд №8)

-Мы можем составить первое уравнение?

-Мы можем составить второе уравнение?

-Составим систему.(Слайд № 9)

-А решать мы ее будем двумя способами.

-Разделимся на две группы

(Решаем систему на формате А3)

-Мы решили задачу?

-Что спрашивается в задаче?

Ответ.(Слайд № 10)

-Давайте с вами составим алгоритм решения задач с помощью систем уравнений. (Слайд №11)

-Молодцы. Примените алгоритм в следующей задачи.(Слайд №12,13)

6.Подведение итогов.

-Кто считает алгоритм практичным, удобным?

-Где он вам понадобится?

7.Рефлексия.

-Для кого сегодняшний урок оказался интересным?

-Что самое важное вы запомнили?

(Слайд №14)

-Кто согласен с этим высказыванием?

-Спасибо ребята за урок .Вашу работу я оценила на отлично,на хорошо. А индивидуальные отметки вы заработаете на практических занятиях.

8.Домашнее задание.(Слайд №15)

Абу-р-Райхан ал-Бируни -среднеазиатский ученый-энциклопедист

«Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит».

Задача

Система

Уравнение

Решение задач с помощью систем уравнений

Является ли пара чисел (0;1) решением системы уравнений

Определить для каждой системы уравнений рациональный метод решения:

М етод алгебраического сложения.

М етод подстановки.

Г рафический метод.

Двое рабочих за одну смену изготовили 72 детали. После увеличения производительности первого рабочего на 15%,а второго на 25%,они вмести изготовили 86 деталей. Сколько деталей в смену изготовил первый рабочий до повышения производительности?

деталей за смену

деталей за смену

1 рабочий

X

(до повышения производительности)

2 рабочий

y

1,5X

(после повышения производительности)

1,25y

72

86

x+y=72

1,15x+1,25y=86

y=32

32(д)-за смену изготавливал 2 рабочий до повышения производительности

x=40

40(д)-за смену изготавливал 2 рабочий до повышения производительности

Ответ: 40 деталей.

• О чем речь?
• Таблица, схема или рисунок.
• x и y.
• 1 уравнение.
• 2 уравнение.
• Система.
• Способ решения.
• Ответ.

Алгоритм решения задач

Молодцы !

Домашнее задание

§7 №7.4;7.13

Спасибо за внимание!