«Решение задач с параметрами в итоговом повторении курса алгебры»

Презентация темы «Решение задач с параметрами в итоговом повторении курса алгебры»

Разработано учителем математики гимназии №22 Захарьян А. А.

Оглавление

• Предисловие 3
• Занятие №1 4-20
• Занятие №2 21-29
• Занятие №3 30-42

Предисловие

• В последнее время в билетах вступительных экзаменов по математике, в ЕГЭ обязательно встречаются задачи с параметрами. Однако эта тема не входит в программу школьного курса за исключением классов с углублённым изучением математики. Существует мнение, что решение задачи с параметрами не выходит за пределы программы школьного курса математики. Имеется в виду, что если ученик или абитуриент владеет школьной программой, то он может самостоятельно, без специальной подготовки справится с задачей с параметрами. На самом деле решить задачу с параметрами может учащийся, который прошел специальную целенаправленную подготовку. Поэтому в школьной математике этим задачам должно уделяться внимание.
• В классах с углублённым изучением математики параметрам уделяется достаточно внимания, начиная с решения линейных уравнений. При изучении каждой темы «углублёнки» можно найти время для решения задач с параметрами. Чего нельзя сказать об общеобразовательных классах и классах с гуманитарным уклоном. Поэтому я предлагаю учителям, работающим в неспециализированных выпускных классах перед итоговым повторением уделить несколько часов решению задач с параметрами

Занятие №1 (2 часа)

• Главное, что должен усвоить школьник это то, что параметр – это число, хоть и неизвестное, но фиксированное, имеющее двойственную природу. После этих вступительных слов можно спросить у школьников встречались ли они с параметрами. Это линейная функция y = kx + b , где x и y – переменные, k и b – параметры; квадратное уравнение ax 2 + bx + c =0, где x - переменная a , b , c , - параметры.
• Задачи надо начинать решать с очень простых, постепенно усложняя их.

0, 5 a а 5 a 2) если а=0, то –а=0, 5а=0, значит –а=5 а 3) если а0, то –а0, значит –аОтвет : если a 5 a если а=0, то–а=5а если а=0, то–а=5а если а=0, то–а=5а если а=0, то–а=5а если а0, то–а" width="640"

Пример №1. Сравнить – а и 5 а

• Решение:

• 1) если а а 0, 5 a а 5 a
• 2) если а=0, то –а=0, 5а=0, значит –а=5 а
• 3) если а0, то –а0, значит –а

• Ответ : если a 5 a

если а=0, то–а=5а

• если а=0, то–а=5а
• если а=0, то–а=5а
• если а=0, то–а=5а

• если а0, то–а

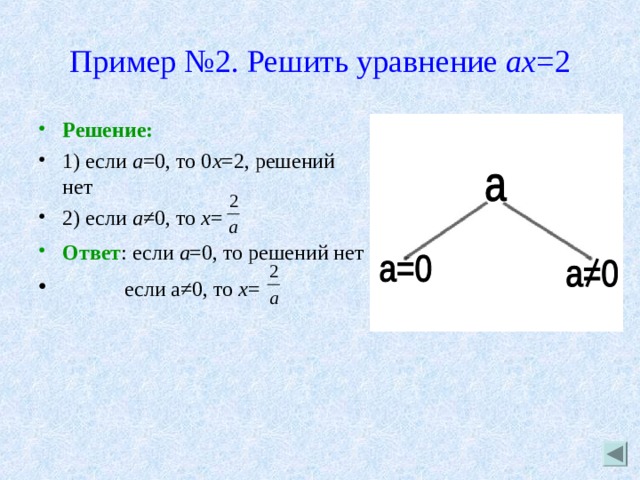
Пример №2. Решить уравнение ах =2

• Решение:

• 1) если а =0, то 0 х =2, решений нет
• 2) если а ≠0, то х =

• Ответ : если а =0, то решений нет

• если а≠0, то х =

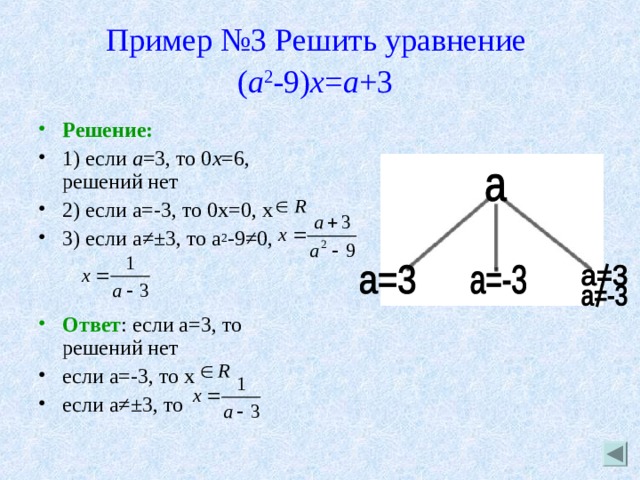
Пример №3 Решить уравнение ( а 2 -9) х = а +3

• Решение:

• 1) если а =3, то 0 х =6, решений нет
• 2) если а=-3, то 0х=0, х
• 3) если а≠±3, то а 2 -9≠0,

• Ответ : если а=3, то решений нет

• если а=-3, то x
• если а≠±3, то

0, то 2) если а 3) если а =0, то - «И» Ответ : если а 0, то х если а если а =0, то " width="640"

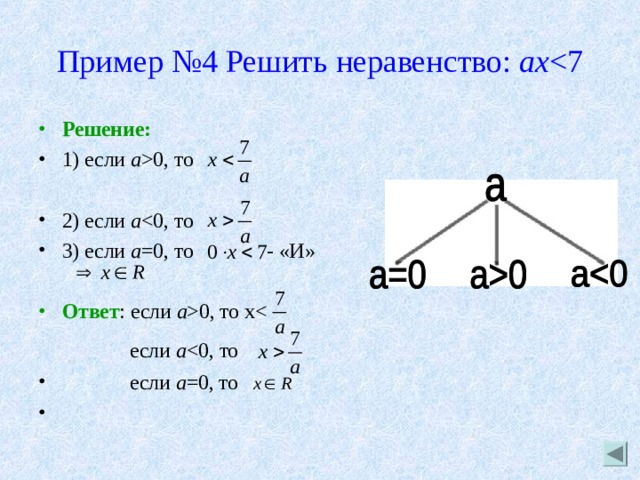
Пример №4 Решить неравенство: ах

• Решение:

• 1) если a 0, то
• 2) если а
• 3) если а =0, то - «И»

• Ответ : если а 0, то х

если а

• если а =0, то

Пример №5 Решить уравнение

• Решение:

• Ответ : если а =-3, то решений нет

если а ≠-3, то х= а .

Пример №6 Решить уравнение

• Решение:

• 1) если а =-1, то -2 х +1+1=0; х =1
• 2) если а ≠-1,то х =1 или

• Ответ : если а =-1, то х =1

если а ≠-1,то х =1 или

-4, то x = b . " width="640"

Пример №7 Решить уравнение

• Решение:
• Ответ : если b x =-4 или x = b

• если b =-4, то x =-4
• если b -4, то x = b .

Пример №8 Решить уравнение

• Решение:

• 1) если а ≠0, то х =1
• 2) если а =0, то x значит х =1 или х =-1

• Ответ: если а ≠0, то х =1

если а =0, то х =±1

Пример №9 Решить неравенство

• Решение:

1) a) если b =1, то

б) если b =-1, то

• б) если b =-1, то

2) если b ≠± 1, то неравенство квадратное

• 2) если b ≠± 1, то неравенство квадратное

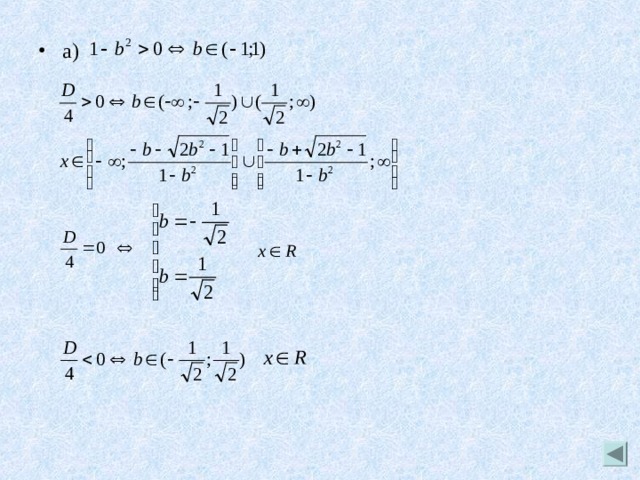
• a)

• б)
• учитывая, что при

• то

• Ответ: если b =1, то

• если b =-1, то

• если то

• если то
• если то
• Рассмотренные выше задачи требовалось просто решить. В следующих задачах будет поставлено какое-то более «узкое», конкретное условие.

Пример №10 При каких а уравнение имеет единственное решение?

• Решение:

• 1) если а =0, то х =3
• 2) если а ≠0, то уравнение квадратное и оно имеет единственное решение при D =0
• D =1-12 a

• Ответ: при а=0 или а=

Пример №11 При каких а уравнение имеет единственное решение?

• Решение:

• 1) если а =2, то решений нет
• 2) если а ≠2, то уравнение имеет единственное решение при D =0

• Ответ: при а =5

Задачи для самостоятельного домашнего решения задаются с ответами для самоконтроля

• При каких а уравнение имеет решения, найти их

при

2) Решить уравнение:

a )

(при а =1 или а =3 решений нет; при а ≠1 и а ≠3 х=а )

• б)

• (при а =-2 решений нет; при а ≠-2 х =2)

3) При каких а уравнение имеет ровно три корня

(при )

Занятие №2 (2 часа)

• Урок начинается с разбора домашнего задания. Затем учитель предлагает решить более общую задачу.

Пример №12 Выяснить, при каких значениях параметра а уравнение имеет:

• 1 ) два различных корня;

• 2) не более одного корня;
• 3) два корня различных знаков;
• 4) два положительных корня .

0. 2) а) если а =4, то б) б) " width="640"

• Решение:

• 1) уравнение имеет два различных корня тогда и только тогда, когда оно квадратное и D 0.
• 2) а) если а =4, то

б)

• б)

• 3) уравнение имеет два корня различных
• знаков тогда и только тогда, когда значит
• 4) уравнение имеет два положительных корня тогда и только тогда, когда

Самостоятельная работа. Вариант I

• 1. Для всякого а решить уравнение

• Решение:

• Т.к. сумма коэффициентов равна 0, то х =1 или х =2 а

• Ответ: 1; 2 а .

• 2. При каких b уравнение имеет единственный корень? Для каждого b найти этот корень.

• Решение:

• Квадратное уравнение имеет единственный корень тогда и только тогда, когда D =0

• 1) если b =12, то
• 2) если b =-12, то

• Ответ: при b =12 x =-2

• при b =-12 x =2.

• 3. Для каждого значения параметра решить неравенство:

• Решение:

• Решим неравенство методом интервалов, рассмотрев функцию f ( x )= ,
• непрерывную на R , имеющую нули 2, -2, b
• Рассмотрим три случая:
• 1)

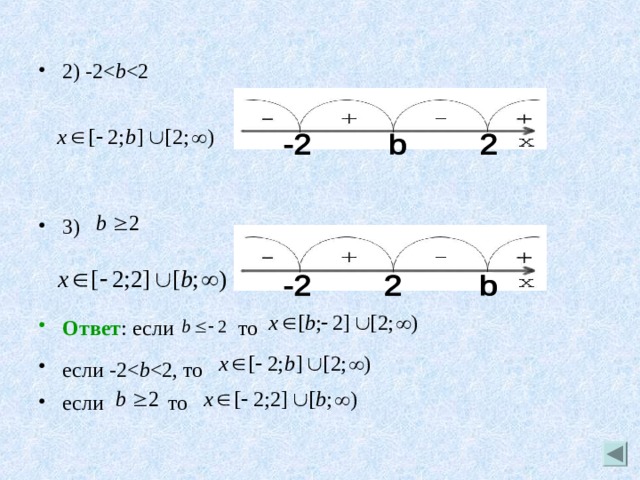
• 2) -2b
• 3)

• Ответ : если то

• если -2b
• если то

Вариант II

• Задания аналогичны заданиям варианта I .
• 1.

• Ответ: -1; 3 а .

• 2.

• Ответ : при b =20 x =-2

• п ри b =-20 x =2.
• 3.

• Ответ: если то

• если -1a
• если то

Занятие №3 (2 часа)

• Теперь можно приступать к решению задач ЕГЭ с параметрами.

Пример №1. Найти все значения параметра p , при которых уравнение имеет хотя бы один корень.

• Решение:

• Рассмотрим функцию f ( a )= определённую на [-1;0) U (0;1] и найдём её область значений.
• f (-1)=11; f (1)=3; при
• f ’( a )=

• f ’( a )=0

• Т.к. то экстремумов у функции нет, следовательно E ( f )= (0;11].
• Чтобы уравнение а значит и данное уравнение имело хотя бы один корень, необходимо и достаточно, чтобы

• Ответ :

Пример №2. Найти все значения а, при которых область определения функции содержит ровно одно двузначное натуральное число .

• Решение:

• D ( y ) :
• Решим первое неравенство системы:

• 1) если 0 a

• Решение не удовлетворяет условию задачи.

1 , то Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы Ответ: " width="640"

• 2) если а 1 , то

• Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы

• Ответ:

Пример №3. Найти все значения параметра а , при каждом из которых множество решений неравенства содержит какой-нибудь отрезок длиной 2,но не содержит никакого отрезка длиной 3

• Решение:

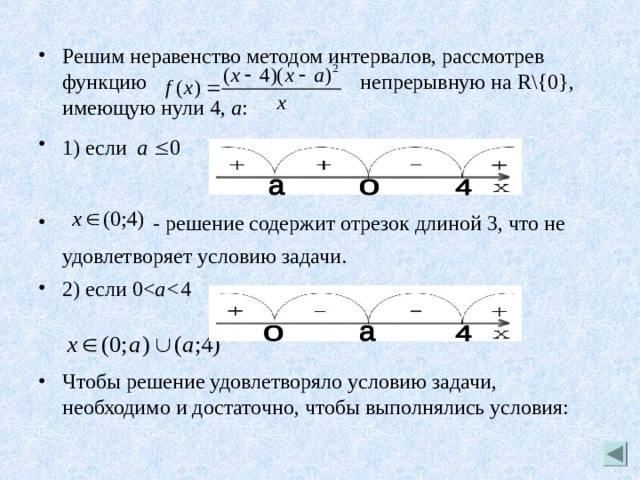
• Решим неравенство методом интервалов, рассмотрев функцию непрерывную на R \{0}, имеющую нули 4, а :
• 1) если

• - решение содержит отрезок длиной 3, что не удовлетворяет условию задачи.
• 2) если 0 a 4
• Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы выполнялись условия:

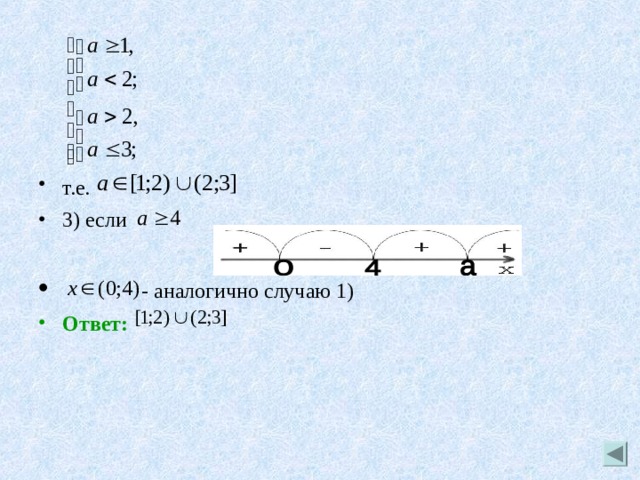
• т.е.
• 3) если

• - аналогично случаю 1)

• Ответ:

Пример №4 . Найти все значения параметра p , при которых уравнение имеет хотя бы один корень, и число различных корней этого уравнения равно числу различных корней уравнения

• Решение:

• 1)
• Пусть =t, тогда

• Рассмотрим функцию
• D ( f )=[0; ),
• f ( t )=0 t =0 .
• E ( f )=(- ;0 ]
• f ’ ( t )= f ’ ( t )
• Значит графики функций и y = p могут иметь только одну общую точку, т.е. уравнение
• а значит и уравнение
• может иметь ровно один корень при

• 2) Узнаем при каких p уравнение
• имеет ровно один корень:
• а) если 2 p +3=0 ( ), то -удовлетворяет условию.
• б) если то уравнение имеет единственный корень при D =0.
• D =0

• Итак, уравнение имеет ровно
• один корень при

• Но уравнению удовлетворяют только
• т.е. при и p =-1 уравнения и
• имеют равное число корней, а именно, по одному.

• Ответ: ; -1