"Решение уравнений с модулем".

Способы решения уравнений, содержащих модуль.

Решим аналитически и графически уравнение:

lх-2l=3

Аналитическое решение

1-й способ

0 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 . Таким образом, получаем, либо х-2=3, либо х-2=-3. Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1. " width="640"

Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т.е. х-20 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 .

Таким образом, получаем, либо х-2=3, либо

х-2=-3.

Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1.

2-й способ

Установим, при каких значениях х, модуль равен нулю: х-2=0, х=2. Получим два промежутка, на каждом из которых решим уравнение. 2 Х

Получим две смешанные системы: х2, -(х-2)=3 х-2=3 Решим каждую систему: х2 х=-1 х=5 Ответ: х 1 =-1, х 2 =5.

Графическое решение.

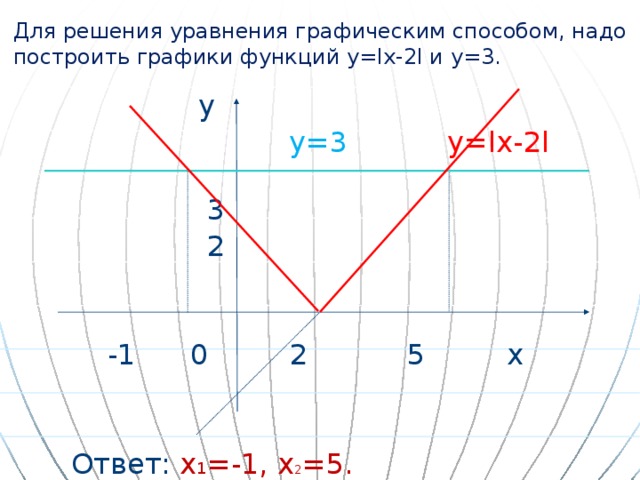
Для решения уравнения графическим способом, надо построить графики функций у=lх-2l и у=3.

у

у=3 у=lх-2l

3

2

-1 0 2 5 х

Ответ: х 1 =-1, х 2 =5.

Решим аналитически и графически уравнение

1+lхl=0,5

Аналитическое решение:

1+lхl=0,5,

lхl=0,5-1,

lхl=-0,5

Ответ: решений нет.

Графическое решение:

Преобразуем уравнение 1+ lхl=0,5.

Получим lхl=-0,5

Графиком функции у= lхl являются лучи – биссектрисы 1-го и 2-го координатных углов.

Графиком функции у=-0,5 является прямая, параллельная оси ох и проходящая через точку -0,5 на оси оу.

Ответ: решений нет.

Решение при помощи зависимостей между числами а и b, их модулями и квадратами этих чисел.

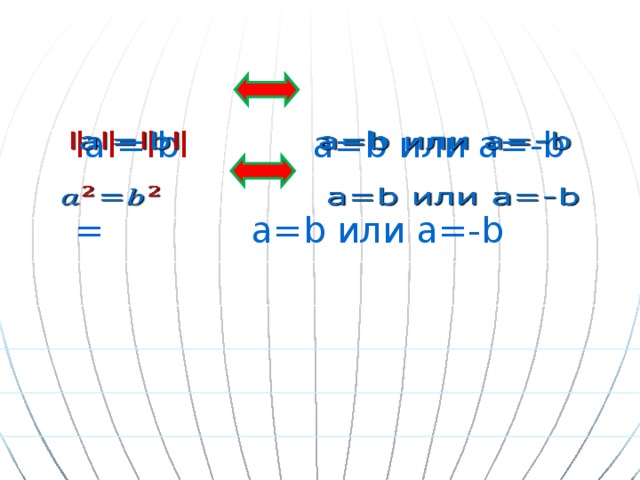
l a l = l b l a=b или a=-b = a=b или a=-b

Решим уравнение l x+1 l = l 2x-5 l двумя различными способами.

1-й способ

Учитывая первое соотношение получим:

Х+1=2х-5 х+1=-2х+5

х-2х=-5-1 х+2х=5-1

-х=-6 3х=4

х=6 х=1

Таким образом корни уравнения: х 1 =6, х 2 = 1

2-й способ В силу второго соотношения имеем = Решив это уравнение, получим: х 1 = 1 , х 2 =6 Ответ: х 1 = 1 , х 2 =6

Графики простейших функций, содержащих знак абсолютной величины

Алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n+1 прямолинейного отрезка.

Тогда график может быть построен по n+2 точками, n из которых представляют собой корни внутримодульных выражений, ещё одна произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя – с абсциссой, большей большего из этих корней.

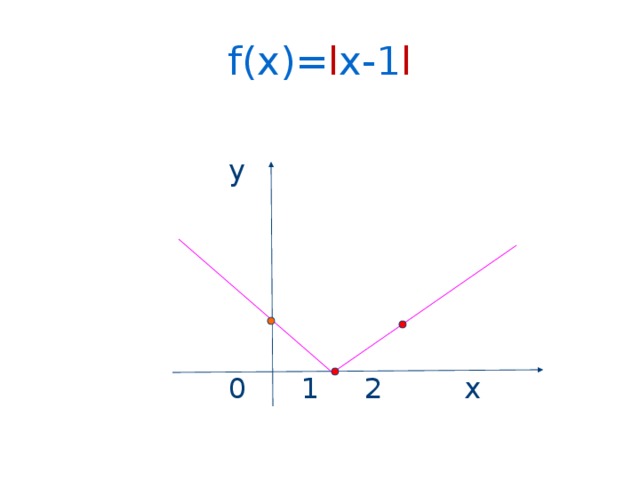
f(x)= l x-1 l

у

0 1 2 х

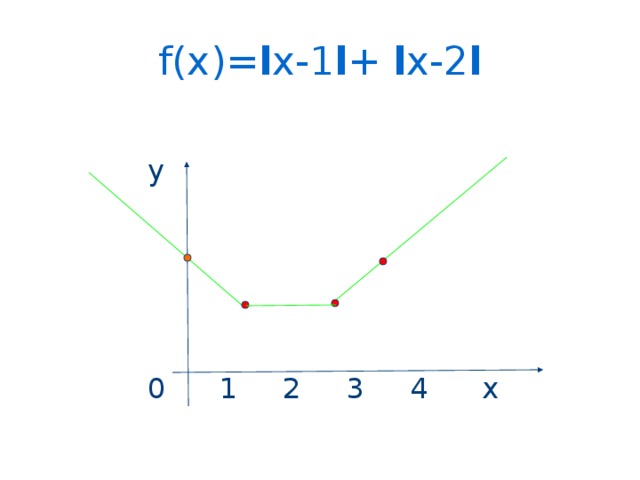
f(x)= l x-1 l + l x-2 l

у

0 1 2 3 4 х

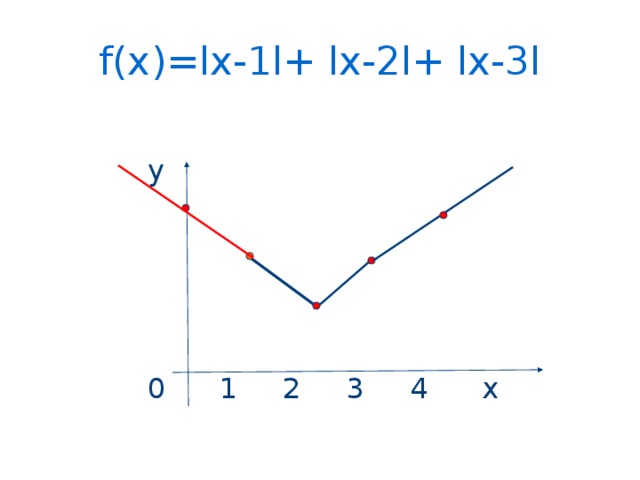
f(x)=lx-1l+ lx-2l+ lx-3l

у

0 1 2 3 4 х

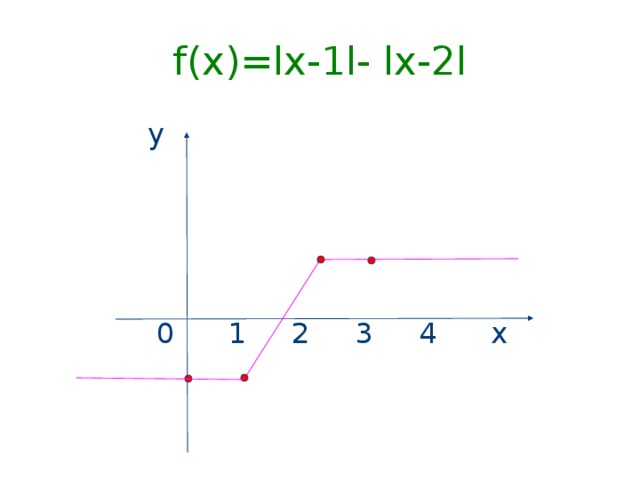
f(x)=lx-1l- lx-2l

у

0 1 2 3 4 х

конец