ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ КЕМЕРОВСКОЙ ОБЛАСТИ
Государственное образовательное учреждение среднего профессионального образования
Кемеровский профессионально-технический техникум
Геометрическая и алгебраическая интерпретация математических понятий
реферат
Выполнил преподаватель математики:
Коровина Нина Анатольевна.
Кемерово 2013
Содержание.
Введение 3
Математические утверждения 4
2. Геометрический метод алгебраических задач 4
2.1. Решение уравнений и неравенств с модулем 4
2.2. Решение систем неравенств 7
2.3. Решение квадратных уравнений 8
2.4. Решение иррациональных уравнений и неравенств 9
2.5. Решение текстовых задач 11
2.6. Решение задач на наибольшее и наименьшее значения функции 12
2.7. Решение задач на нахождение площади фигуры, заданной на координатной плоскости 14
2.8. Преобразование графиков 16
Заключение 18
Литература 19
Введение
Софии Жермен: «Алгебра – не что иное, как записанная в символах геометрия, геометрия – это просто алгебра, воплощенная в фигурах».
В арсенале каждого учителя имеются «маленькие хитрости» - это и методические приемы объяснения, способствующие лучшему пониманию и усвоению школьниками учебного материала, и способы решения некоторых задач, помогающие ученикам избежать рутинной работы и упростить громоздкие выкладки и вычисления.
Существуют способы решения алгебраических задач методами,
основанными на наглядно-геометрических интерпретациях. «В целом почти всю математику можно рассматривать как развивающуюся из взаимодействия алгебры (первоначально арифметики) и геометрии, а в смысле метода - из сочетания выкладок и геометрических представлений» (А.Д.Александров).
История математики свидетельствует о том, что оба метода, алгебраический и геометрический развивались в тесной взаимосвязи. В классическую греческую эпоху геометрия занимала привилегированное положение. Она являлась именно той наукой, в которой проявлялся дедуктивный характер рассуждения, искусство доказательства. Первые элементы алгебры появились сразу в интерпретациях: геометрический и буквенно-символической. Систематизация алгебраических сведений построение алгебры как особой части математики проходило также в двух равносильных и равноправных интерпретациях. Этот набор методов было принято называть геометрической алгеброй. Благодаря взаимосвязи алгебраического и геометрического методов были сделаны многие открытия в математике.
Геометрический метод состоит в том, что само доказательство или решение задачи направляется наглядным представлением. Основное
преимущество геометрического метода в его наглядности. Он позволяет увидеть то, что в алгебраическом методе скрыто за аналитическими выкладками. Кроме того, выполненный рисунок позволяет рассуждать, делать выводы. Недаром еще великий Р. Декарт в своем труде «Правила для руководства ума» специально выделял правило о том, что «полезно чертить фигуры и преподносить их внешним чувствам, для того,
чтобы таким образом нам было легче сосредоточивать внимание нашего ума».
Геометрия - уникальный школьный предмет, внутри которого заложены богатейшие возможности развития логического мышления и пространственного воображения. Почему же этот потенциал, как правило, не используется на уроках алгебры? Зачастую алгебру и геометрию вообще воспринимают как два различных предмета, забывая о том, что это составляющие одного целого.
Цели данной работы:
1. Показать, что преимущество геометрического решения алгебраических задач в его наглядности, так как геометрический подход допускает изящное решение.
2. Выявить связи между, казалось бы, совершенно разнородными темами школьного курса математики.
Задачи:
Рассмотреть ряд приёмов решения нестандартных и конкурсных
задач.
Практическая помощь учителям математики.
Математические утверждения
Между алгебраическими и геометрическими задачами, между языком алгебры (языком формул) и языком геометрии (языком расстояний) существует неразрывная связь, ставшая со времен Декарта очевидной даже тем, кто не слишком искушен в математике. В самом деле, решение многих геометрических задач может быть сведено к решению систем алгебраических уравнений и требует умения применять соответствующий алгебраический инструмент.
Менее заметны, особенно школьнику, геометрические идеи, лежащие в основе решения ряда алгебраических задач: на вычисление наибольших и наименьших значений некоторых выражений, решение уравнений и неравенств. Вероятнее всего, это связано с тем, что алгебраический язык является для школьника своего рода первым математическим языком, а геометрический язык - вторым.
Изучение языка невозможно начать без словаря или хотя бы разговорника. В нашем случае этот словарь - разговорник довольно прост: в нем всего три строчки
| Алгебраический язык (язык формул) | Геометрический язык (язык расстояний) |
| Числа и буквы | Расстояния до координатных осей (координаты) |
| Модуль разности двух чисел | Расстояние между двумя точками координатной прямой |
| Сумма квадратов двух чисел | Квадрат расстояния между двумя точками координатной плоскости |
2. Геометрический метод алгебраических задач
2.1. Решение уравнений и неравенств с модулем.
Напомним, что модуль разности двух чисел равен расстоянию между точками числовой (координатной) прямой, соответствующими этим числам (в этом, собственно, и заключается геометрический смысл модуля). Так, |а - b| есть расстояние между точками а и b числовой прямой; |а=|а-0| - расстояние между точками а и 0; |а + b| = |а -(-b)| - расстояние между точками а и -b.
Решить уравнение |х - b|=а - значит найти все точки х числовой оси, расстояние от каждой из которых до числа b равно а. Возможны три случая; если а 0, то х = b±а; если а=0, то х=b; если а
Решение уравнения |f(x)|=a при а0 сводится к рассмотренному случаю после замены переменной: f(x)=t. При решении конкретных примеров такую замену можно не делать и сразу переходить к уравнениям f(x)=a; f(x)--a.
Аналогично решается уравнение |f(x)|=g(x). Действительно, если g(x)оно не имеет решений ( в силу не отрицательности модуля); если g(x) 0, то f(x)=g(x); f(x)=-g(x).
Другой способ решения состоит в рассмотрении двух случаев при освобождении от знака модуля: |f(x|=f(x) при f(x) 0, |f(x|--f(x) при f(x)корни полученных уравнений и проверить , какие из них удовлетворяют соответствующему неравенству.
Как видим, решение уравнения |f(x)|=g(x) уже не требует использования геометрического смысла модуля (хотя им можно воспользоваться при обосновании полученной схемы решения).
Рассмотрим еще одно уравнение вида |х - b|+|х - с| = а при решении которого использование геометрического смысла модуля достаточно эффективно. Решить уравнение |х - b| + |х - с |= а - значит найти все точки х числовой оси, сумма расстояний от каждой из которых до точек bис равна а.
Если расстояние между точками bис больше а, то уравнение не имеет решений. В самом деле, если предположить, что искомая точка принадлежит отрезку с концами b и с, то сумма расстояний от такой точки до концов отрезка окажется больше а (поскольку длина этого отрезка больше а), а для любой точки, лежащей вне рассматриваемого отрезка, сумма расстояний будет еще больше.
Если расстояние между точками bис равно а , то любая точка с концами bис будет решением данного уравнения.
Если же расстояние между точками bис меньше а, то для любой точки отрезка с концами bис сумма расстояний до точек bис будет меньше а. Таким образом , искомая точка должна лежать вне отрезка с концами b и с. В этом случае сумма расстояний от искомой точки до точек bис будет складываться из длины отрезка с концами b и с и удвоенного расстояния от этой точки до ближайшего к ней конца отрезка. Это рассуждение и позволяет найти искомые значения переменной.
Задание 1
«Переведем» следующие предложения с геометрического на алгебраический.
| Язык расстояний | Язык формул |
Расстояние от точки t числовой оси до точки -22 меньше 5 | │t+ 22│˂ 5
|
Сумма расстояний от точки х числовой оси до точек -3 и 5 равно 12 | │х+3│+│х-5│=12 |
Точка 5 числовой оси равноудалена от точек х-1 и х2-16 | │х-6│=│ х2-21│ |
Расстояние от точки М прямой y=3х – 2 до оси ординат | │3х– 2│=5│х│ Указание. Расстояние от точки (х;y)графика функции y=f(x) до осей абсцисс и ординат равно │f(x) │и│х │соответственно |
Точка М(а;б) принадлежит окружности с центром в начале координат и радиусом 3 | а2 +в2=9 |
Сумма расстояний от точки М (х;у) до точек А(3;4) и В(-2;5) не больше 6 | 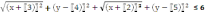
|
Расстояние от точки М (m;n)единичной окружности до точки Р(-4;1) равно 3 | 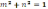
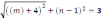
|
Расстояние от точки М(р;q) окружности с центром А(-2;-4)и радиусом 2 до точки Р(а;b) окружности с тем же центром и радиусом равным 6 равно 8 | (p+2)2+(q+4)2=4 (a+2)2+ (b+4)2=36 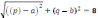
|
Сумма расстояний от точки М прямой у=2х-1 до точек Р(3;4) и Е(-1;1) равно 5 | 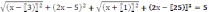
|
Расстояние от точки М прямой у=х до точки Р прямой у=2х-3 не меньше 9 | 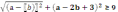
|
Задание 2.
«Переведем» следующие предложения с алгебраического языка на геометрический.
| Язык формул | Язык расстояний |
| 1.Решите уравнение |х - 5 | =2 |х + 3|. | 1 .Найдите все точки х числовой оси, расстояние от каждой из которых до точки 5 в 2 раза больше расстояния до точки 3. |
| 2.Имеет ли система  р2 + а2 = 16 г2 + t = 25 (р- r)2+(q- t)2 = 100 хотя бы одно решение? | 2.Можно ли на каждой из концентрических окружностей с центром в начале координат, радиусы которых равны 4 и 5 . найти по точке, расстояние между которыми равно 10? |
| 3.Найдите наименьшее значение функции y=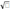 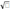 (x-l)2 + 9+ (x-l)2 + 9+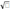 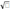 (x + 3)2+16 (x + 3)2+16 | З.На оси абсцисс найдите точку, сумма расстояний от которой до точек (1 ;3) и (-3;4) минимальна. |
| 4.Найдите наименьшее значение функции; у= 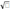 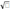 (х+2)2 + ( 2х + 1 )2 + (х+2)2 + ( 2х + 1 )2 + 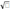 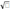 (x - З)2 + ( 2х -5 )2 (x - З)2 + ( 2х -5 )2 | 4.На прямой у=2х найдите точку, сумма расстояний от которой до точек (-2; -1) и (3:-5) минимальна. |
| 5.Решите неравенство (z - x)2+(z – 3x+5)2 ≤18
| 5. На прямых у=х и у=Зх-5 найдите все точки такие, что квадрат расстояния между точкой первой прямой и точкой второй прямой не превосходит 18. |
| 6. Решите уравнение |х| = 5| ах - 3|. | 6. На графике функции у=ах-3 найдите все точки, расстояние от каждой из которых до оси ординат в 5 раз больше расстояния до оси абсцисс |
| 7.Найдите все значения а , при каждом из которых система 
( m - З)2 +( n - 4) = а2 m2 + n2=4
имеет единственное решение. | 7.Найдите радиус окружности с центром в точке (3;4), если известно, что эта окружность касается окружности с центром в начале координат и радиусом равным
|
При выполнении этого задания важно обратить внимание учащихся на то, что условие принадлежности некоторой точки М той или иной фигуре (например, прямой или окружности), заданной уравнением , может быть записано с помощью различных букв, а не только с помощью букв х и у. Так, равенства ( р-3)2 + ( q + 2)2 = 16 и ( m - 3) + ( п + 2)2 = 16 означают, что и точка (p;q), и точка (т ; п) принадлежат окружности с центром ( 3 ; - 2) и радиусом 4, т. е. окружности (х - З)2 + (у+2)2 = 16 координатной плоскости Оху.
2.2. Решение систем неравенств.
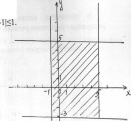 1.Решим систему неравенств:
1.Решим систему неравенств:

|х-2|≤3
|у-1|≤1
 Решение:
Решение:
-3 ≤ х-2 ≤ 3
-4 ≤ у-1 ≤ 4

 -1 ≤ х ≤ 5
-1 ≤ х ≤ 5
-3 ≤ у ≤ 5
Решением системы неравенств являются все координаты точек замкнутой области (прямоугольника) и ее границы.
2.Решим систему неравенств:
х2 + у2 ≤ 9
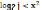
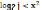
Решение:

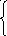 х2 +у2≤ 9, х2 +у2 ≤ 9,
х2 +у2≤ 9, х2 +у2 ≤ 9,
у0, у2х2;
у2х2
х2+у2=9 – окружность с центром в точке О(0;0) и R=3.
Решением системы являются координаты точек заштрихованной части плоскости ( координаты точек окружности являются решением).
у
2.3. Решение квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра квадратные уравнения решали не алгебраически , а геометрически.
Уравнение, которое решали древние У2 + 6у-16=0.
У2+6у-16=0 или у2+6у+9= 16+9
Выражения у
2+6у+9 и 16+9 геометрически представляют собой один и тот же квадрат, а исходное уравнение и уравнение У
2+6у -16 +9-9=0 -одно и то же уравнение. Откуда и получаем, что у+3=±5, или у
1=2 , у
2 = -8. Ответ: -8;2.
Решение квадратных уравнений с помощью циркуля и линейки.
Предлагаем следующий способ нахождения корней квадратного уравнения ах2 +вх+с=0 с помощью циркуля и линейки.
Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1;0) и Д(х2;0), где х1| и х2 -корни уравнения, и проходит через точки А(0;1) и С(0;с/а) на оси ординат. Тогда по теореме о секущих имеем В ● ОД=ОА ● ОС, откуда ОС=(ОВ ●ОД)/ОА=( х, ● х2)/1=с/а. Центр окружности находится в точке в точке пересечения перпендикуляров ME и МК, восстановленных в серединах хорд АС и ВД, поэтому МК=( х,+ х2 )/2=-в/2а,
МЕ=(у1+ у2 )/2=(1+с/а)/2=(а+с)/2а.
Итак: 1) Построим точки М(-в/2а; (а+с)/2а) (центр окружности) и А(0;1);
2) Проведем окружность с радиусом МА;
Абсциссы точек пересечения этой окружности с осью Ох являются
3)корнями исходного квадратного уравнения
При этом возможны 3 случая:
1) Радиус окружности больше ординаты центра АММК, окружность
пересекает ось Ох в двух точках В(Х|;0) и Д(х2;0), где xt и х2 -корни
квадратного уравнения. ( Рис. 1 (a)).
( Рис. 1 (a)).
2.4 Решение иррациональных уравнений и неравенств.
Пример 2. Решить неравенство 

 Решение. 1. Алгебраический метод. Данное неравенство равносильно
Решение. 1. Алгебраический метод. Данное неравенство равносильно
совокупности двух систем:

1-х≥0 1-х˂0
х(1-х)2 и х ≥ 0


Решая эти системы, находим:




и 







и
Решением первой системы является промежуток 
 , а второй
, а второй
системы х 1. Объединяя эти решения, получаем ответ. Ответ: 

Решение 2. Геометрический метод. Построим в прямоугольной системе координат графики функций y1 = 
 и у2= 1 - х. На геометрическом языке, решить неравенство
и у2= 1 - х. На геометрическом языке, решить неравенство
 1 – х значит найти те значения х, при которых график функции у расположен выше графика функции у .
1 – х значит найти те значения х, при которых график функции у расположен выше графика функции у .
Как видно на рисунке, корень уравнения
 = 1 - х единственный и он лежит в интервале (0;1). Найдём его аналитически, решив уравнение
= 1 - х единственный и он лежит в интервале (0;1). Найдём его аналитически, решив уравнение
х=(1-х)2
х2-3х+1=0,
откуда х1= 
 , х2=
, х2= 

Так, как х1= 
 , х1, то этот корень посторонний. Итак, х=
, х1, то этот корень посторонний. Итак, х= 

Рисунок показывает, что график функции у1=
 лежит выше прямой у2=1-х на промежутке х
лежит выше прямой у2=1-х на промежутке х 
 Ответ: х
Ответ: х 

В данном случае геометрический метод решения представляет собой
единство графического метода и метода уравнений и неравенств (так как
корни находим аналитически).
2) Радиус окружности равен ординате центра АМ=МВ, окружность
касается оси Ох в точке В(х 1;0), где х1 -корень квадратного
уравнения, (рис. 1(б)).
3) Радиус окружности меньше ординаты центра АМне имеет общих точек с осью абсцисс, в этом случае уравнение не
имеет решения.(Рис.1(в)).
Рис.1(б) Рис.1 (в)
Примеры.
1) Решим уравнение: х2 -2х-3=0.
Решение. Определим координаты точки центра окружности по формулам
х=-в/(2а)=2/(2 ●1)=1, у=(а+с)/(2а)=(1-3)/2= -1.
Проведем окружность радиуса МА, где А(0;1). Окружность пересекает ось
Ох в точках В(-1 ;0) и Д(3;0).
Ответ: -1; 3.
2) Решим уравнение: х2-2х+3=0.
Решение. Определим координаты точки центра окружности М (х;у)
х=-в/(2а)= 2/2=1, у=(а+с)/(2а)=(3+1)/2=2.
Проведем окружность радиуса МА, где А(0;1). Окружность не пересекает
ось Ох.
Ответ: нет решения
3) Решим уравнение: х2 -6х+9=0.
Решение. Определим координаты точки центра окружности М(х;у)
х= -в/(2а)= 6/2=3, у=(а+с)/(2а)=(9+1)/2=5.
Проведем окружность радиуса МА, где А(0;1). Окружность касается
оси Ох в точке В(3;0). Ответ: 3.
2.5 Решение текстовых задач
Среди текстовых задач встречаются задачи, которые нельзя решить алгебраическим методом, и которые могут быть решены различными методами, в том числе и геометрическим
Примеры:
1.В 7ч. утра пассажирский самолет вылетел из города А. После получасовой остановки в городе В в 8ч10мин самолет сделал поворот на 35 вправо и в 9ч совершил посадку в городе С. Найти расстояние между городами А и С, если средняя скорость самолета на каждом участке полета была равна 320 км/ч
Дано: ˂СДВ=а=350;
V=320км/ч
t1=8ч 10 мин;
t2=9ч;
t3=30мин;
t0=7ч;
Найти АС.
Решение:
АВ = V(t1-t0-t3); АВ =320*2/3=213,3 (км)
ВС= V(t2- t1); ВС=320*5/6=266,6 (км)
˂ АВС=1800 – 350=450; ( по т. косинусов);
АС2=ВС2 – 2АВ*ВС*

АС2=213,32+266,62+2*213,3*266,6*
 АС= 458 км.
АС= 458 км.
Ответ: 458км.
2. Разность двух чисел равна 16. Если каждое из чисел увеличить на 6, то их произведение увеличится на 396. Какие это числа?
Решение: (метод прямоугольника)
| М Р
S1 6 | О 36 |
| D a
b b
A a B | c k
b
6 E |
Пусть отрезки АВ и АД - искомые числа. Площадь прямоугольника АВСД - прежнее произведение чисел. Отрезки АЕ и AM- увеличенные числа, а площадь прямоугольника АЕОМ - увеличенное произведение. Числу 396 соответствует площадь фигуры ДСВЕОМД. Площадь квадратика СКОР равна 36, тогда S,+S2= 396-36=360. Прямоугольники МДСР и ВСКЕ взятые вместе и сложенные дают прямоугольник с размерами а+в и 6, а его площадь 360, так что а+в=360:6=60.
 а 16 Сейчас надо найти два числа, сумма которых 60,
а 16 Сейчас надо найти два числа, сумма которых 60,

 16 а разность 16. Вновь помогает чертеж. (60-
16 а разность 16. Вновь помогает чертеж. (60-
60 16):2=22=в; а=в+16=38
 в Ответ: 38 и 22
в Ответ: 38 и 22
2.6 Решение задач на наименьшее и наибольшее
значение функции
При решении многих таких задач с помощью производной приходим к громоздким вычислениям, да и при вычислении производной сложной функции нет гарантии в том, что ученик не допустит ошибку. Иногда имеет смысл «перевести» условие задачи с языка формул на язык расстояний. Примеры:
1. Найти наибольшее значение функции у = √1-х2 на[-1;1]
Решение:
а) алгебраический метод
Эта задача решается по стандартному алгоритму: у/=-х/(1-х2); у/=0 при х=0; у(-1)=0; у(1)=0; у(0)=1 Ответ: 1
б) геометрический метод

Равенство у = √l –x2 равносильно системе х2+у2=1
у≥0
А значит задает полуокружность с центром О(0;0) и радиусом 1.

у
в
 0
0
-1 1 х
На [-1 ;1] наибольшее значение функции равно 1 при х=0
Ответ:0
«Переведем» на язык расстояний, для этого выделим полные квадраты в подкоренных выражениях: у = √(x-l)2+4 + √(х-8)2+25 . Каждое слагаемое из правой части полученного равенства представляет собой расстояние от т. А(х;0) до некоторой точки с фиксированными координатами, не зависящими от переменной х. Тогда на языке расстояний задачу можно сформулировать так: найдите на оси абсцисс т.А, сумма расстояний от которойдо двух данных точек С и В минимальна.
Если точки В и С лежат по разные стороны от оси абсцисс, то искомая т.А - есть точка пересечения прямой ВС с этой осью. (Если точки В и С лежат по одну сторону, то т.А- точка пересечения прямой В]С с этой осью, где т. В]-точка, симметричная В относительно оси ОХ. В обоих случаях сумма расстояний одна и та же.)
Абсциссы точек В и С известны: 1 и 8, а квадраты ординат разны 4 и 25. Выберем знаки ординат так, чтобы точки В и С оказались лежащими по
разные стороны от оси абсцисс. Рассмотрим, например, точки В(1;-2) и С(8;5). Найдем уравнение прямой ВС:
(х-1)/(8-1)=(у+2)/(5+2); (х-1)/7=(у+2)/7; у=х-3. Тогда абсцисса т.А(х:0) раина З, а искомый минимум равен √(3-l)2+4 + √(3-8)2+25 = 7√2
Ответ: 7√2
3.При каких значениях параметра а модуль разности корней уравнения
х2-6х+12+а2-4а=0 принимает наибольшее значение?
Решение:
а) алгебраический метод:
Решим квадратное уравнение, получим корни x1,2=3±√-3-a2+4a,
тогда |x1-x2 |= 2√-3-a2+4a = 2 √1- а -2)2
Рассмотрим функцию у(а)= 2√1-(a-2)2. Наибольшее значение этой
функции равно 2 и достигается при а=2.
Ответ: 2
Чаще всего, значительная часть учащихся пытается решить задачу с помощью производной и сталкивается с довольно значительными трудностями, связанными с преобразованием иррациональных выражений и дифференцированием сложной функции.
б) геометрический метод:
«Переведем» условие задачи на геометрический язык. Для этого
выделим полные квадраты в левой части уравнения и запишем его в
виде (х-3)2+(а-2)2=1.
Мы получили уравнение окружности в системе координат Оха, его
корни равны абсциссам точек пересечения окружности с прямой,
параллельной оси абсцисс и заданной уравнение а=m. Модуль разности двух чисел- это расстояние между двумя точками координатной прямой. Расстояние между этими точками максимально, если они являются концами диаметра окружности. Таким образом, прямая должна проходить через центр окружности - точку (3;2),
следовательно а=2.
Ответ: 2
4.Найти наибольшее значение функции у(х)=√х2+9 -√x2-x√3+l.
Решение: Рассмотрим треугольник ABC, в котором АС-х; ВС=3; СД=1; лежит во внутренней области треугольника АВ.

По теореме Пифагора из ABC находим AB=√x2+9;

 по теореме косинусов из АСД находим АД=√х2-х√3+1;
по теореме косинусов из АСД находим АД=√х2-х√3+1;
Тогда у(х)=АВ-АД и max у(х)=mах(АВ-АД)= А1В-А1Д=ВД, где А1€ АС
По теореме косинусов из ВСД

Ответ

2.7 Решение задач на нахождение площади фигуры, заданной на координатной плоскости
В последние годы становятся все более популярными задачи, которые не укладываются в какую-нибудь одну традиционную тему. Часто предлагается нарисовать что-нибудь заданное аналитическими условиями.
Решение задачи упрощается, если проводить его используя геометрический метод.
Решения первого неравенства получаем, объединяя решения двух систем



 2) у ˂ 0
2) у ˂ 0
4-х2≥0 4-х2≥у2 или


у
 0 у
0 у
 0
0
│х│≤ 2 х2+у2 ≤ 4


У у




-2 2 х -2 2 х



2

Решения второго неравенства образуют точки, лежащие под графиком функции y=│x+l│+3





Значит фигура, задаваемая условиями задачи имеет вид
Площадь фигуры равна сумме площадей: полукруга с центром 0(0;0) и радиусом 2 (Si), треугольника ACM (S2) и трапеции СДЕМ (S.-?).
S1=2п; S2=0,5*3*3=4?5; S3=(2+3)/2* 1=2,5;
Sфигуры =2п+4,5+2,5=2п+7 Ответ: 2п+7
2.Найдите площадь фигуры, ограниченной линиями х=3/2, х=2, у=√2х-х2.
Решение: Равенство у=√2х-х2 равносильно системе



у≥0 у≥0
у2=2х-х2 = (х-1)2+у2=1
Графиком функции у = √2х-х является полуокружность с центром в т. М(1;0) и радиусом равным 1. Она расположена в верхней координатной полуплоскости.






Искомая площадь равна разности площадей сектора МАВ (S1) и треугольника МАН (S2).
МН=0,5; МА=1; АН найдем по теореме Пифагора АН=√1-1/4=√3/2;
Площадь сектора S1=пR2 а/ 3600 ; S1=п*1*600/3600=п/6;
Площадь прямоугольного треугольника МАН S2=0,5*0,5*√3/2=√3/8;
Sфигуры = п/6-√3/8
Ответ: п/6-√3/8
3.Найти площадь фигуры, ограниченной графиком функции у=√1-х2.
Решение: Равенство у=√1-х2 равносильно системе
у ≥ 0
х2+у2=1
Значит графиком функции у= П-х является полуокружность с центром О(0;0) и радиусом 1, расположенная в верхней координатной полуплоскости.


Площадь полуокружности равна пR2/2.
Площадь искомой фигуры равна п*1/2=п/2. Ответ: п/2
2.8 Преобразование графиков
При построении графиков функций в школьном курсе алгебры часто используются такие геометрические понятия, как симметрия (осевая и центральная), параллельный перенос, отражение и поворот. Известно, что графиком квадратичной функции является парабола, симметричная относительно прямой, график обратной пропорциональности симметричен относительно начала координат и т.д. Простейшие операции над графиками удобно производить по правилам:
1 .y=f(x)+b- параллельный перенос на графика y=f(x) на Ь единиц вдоль оси ординат.
y=f(x+a) - параллельный перенос вдоль оси абсцисс графика
функции y=f(x) на а единиц.
y=f(-x) - отражение графика функции y=f(x) относительно оси ординат.
y=-f(x)- отражение графика функции y=f(x) относительно оси абсцисс.
Приведем примеры построения графиков более сложных функций.
у=(х2-4х+3)2
у1=х2-4х+3; у=у12
Строим график функции у1=х2 - 4х+3. Отмечаем на графике характерные точки - вершину параболы, точки пересечения параболы с осями координат и одну промежуточную точку: );М,(3;0);М2(4;3);-Мз(1;0);
В силу симметрии графика относительно прямой х=2 для построения эскиза достаточно трех точек: Мо; М1 М2.
Возводим в квадрат ординаты этих точек:
а) М0(2;-1): у1 =-1, отсюда y=y12=l, получаем точку К()(2;1);
б) Mi(3;0): у1=0, отсюда у=0, получаем точку
К1(3;0);
в) М2(4;3): у1=3, отсюда у=9, получаем точку
К2(4;9);
Наносим полученные точки на нижний рисунок, соединяем их плавной линией и учитываем симметрию относительно прямой х=2.
2. y=|-xz+4|x|+5|
Строим график функции у=х2+4х+5. Затем выполняем отражения относительно оси ординатой оси абсцисс.
3.На плоскости функция у=f(х) задает семейство кривых, зависящих от параметра а. Каждое семейство обладает определенным свойством. Например: семейство у=f(х;а) – параллельные между собой прямые Семейство вида у-у0=а(х-х0) состоит из прямых с геометрически решать задачи с параметрами.
Задача: Найти все значения параметра к, при котором система уравнений

у-0,5=к(х+2)
у=√х имеет решения.
Прямые семейства у-0,5=к(х) переходят друг в друга путем преобразования поворота с центром в точке (-2;0,5). Данная система будет иметь решение, если прямые имеютс «полупараболой» у=√х хотя бы одну общую точку.
На рисунке отмечены два положения прямой, которым соответсвуют некоторые значения параметра к1 и к2. На первой прямой лежит вершина. Вторая прямая касается «полупараболы». Значение к1найдем, подставив в первое уравнение системы пару (0;0), к1=-1/4.
Значение к2получим, потребовав от системы иметь одно решение.

у-0,5=к(х+2)
у2=х
к0
Система равносильна уравнению ку2-у+0,5+2к=0 при к0, которое имеет один корень при к2=1/4 . Ответ: к2=1/4
4.При каких значениях параметра b уравнение 
 имеет одно решение?
имеет одно решение?
Решение: Область определения:х˂2 и х≠0. Для удобства обозначим 
 Запишем уравнение, равносильное исходному: , а0
Запишем уравнение, равносильное исходному: , а0
Переходим к равносильной системе:



х˂2
х≠0
Строим график функции у=
 Семейство параллельных прямых у=а должно пересекать полученный график только в одной точке.
Семейство параллельных прямых у=а должно пересекать полученный график только в одной точке.
Из рисунка видно, что это требование выполняется лишь при а2, т.е. 

Заключение
Приведённые примеры иллюстрируют интеграцию алгебраического и
геометрического методов в виде их сочетания. Этот способ интеграции
позволяет сравнить между собой алгебраический и геометрический методы,
их силу и эффективность, выявить преимущества и недостатки каждого.
Основное преимущество геометрического метода в его наглядности. Он
позволяет увидеть то, что в алгебраическом методе скрыто за
аналитическими выкладками. Кроме того, выполненный рисунок позволяет
рассуждать, делать выводы. Недаром еще великий математик Р. Декарт в
своём труде «Правила для руководства ума» специально выделял правило о
том, что «полезно чертить ... фигуры и преподносить их внешним чувствам,
для того чтобы таким образом нам было легче сосредоточивать внимание
нашего ума»
В данной работе на конкретных примерах показано, что при решении некоторых алгебраических задач целесообразно применять геометрический метод решения, а иногда это единственный метод, доступный учащимся, так как для решения другим методом у них не хватает запаса знаний на данный момент.
Методы, рассмотренные в этом проекте, рекомендуют учителям математики для применения их на уроках с 5 по 11 класс, как на базовом уровне, так и на профильном. Данная работа поможет коллегам в их практической деятельности.
Литература
Основные источники:
Башмаков, М. И. Математика [Текст] : учеб. для образовательных учреждений, реализующих прогр. нач. и сред. проф. образования / М. И. Башмаков.- 7-е изд., стер.- Москва : ИЦ «Академия», 2013.- 256 с. - [Рекомендовано ФГУ «ФИРО»].
Башмаков, М. И. Математика. Задачник [Текст] : учеб. пособие для образовательных учреждений, реализующих прогр. нач. и сред. проф. образования / М. И. Башмаков.- 2-е изд., стер. – Москва : ИЦ «Академия», 2013.- 416 с. - [Рекомендовано ФГУ «ФИФО»].
Богомолов, Н. В. Математика [Текст] : учеб. для студентов образовательных учреждений сред. проф. образования / Н. В. Богомолов, П. И. Самойленко. – 6-е изд., стер. – Москва : Дрофа, 2009. – 365 с. – [Допущено МО РФ].
Богомолов, Н. В. Сборник задач по математике [Текст] : учеб. пособие для студентов образовательных учреждений сред. проф. образования/ Н. В. Богомолов. – 5-е изд., стер. – Москва : Дрофа, 2009. – 204 с. – [Допущено МО РФ].
Дополнительные источники:
Башмаков, М. И. Математика. Книга для преподавателя [Текст] : методическое пособие для образовательных учреждений, реализующих. программы нач. и сред. проф. образования / М. И. Башмаков. – Москва : ИЦ «Академия», 2013. – 224 с. – [Рекомендовано ФГАУ «ФИРО»].
Богомолов, Н. В. Сборник дидактических заданий по математике [Текст] : учеб. пособие для студентов образовательных учреждений сред. проф. образования / Н. В. Богомолов, Л. Ю. Сергиенко. – 3-е изд., стер. – Москва : Дрофа, 2009. – 236 с. – [Допущено МО РФ].
Григорьев, В. П. Сборник задач по высшей математике [Текст] : учеб. пособие для студентов образовательных учреждений сред. проф. образования / В. П. Григорьев, Т. Н. Сабурова. – Москва : ИЦ «Академия», 2010. – 160 c. [Рекомендовано ФГУ “ФИРО”].
Григорьев, В. П. Элементы высшей математики [Текст] : учеб. для студентов образовательных учреждений сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. – 5-е изд., стер. – Москва : ИЦ «Академия», 2010. – 320 с. – [Допущено МО РФ].
Кочетков, Е. С. Теория вероятностей и математическая статистика [Текст] : учеб. для студентов образовательных учреждений сред. проф. образования / Е. С. Кочетков, В. В. Соколов, С. О. Смерчинская. – 2-е изд., испр. и перераб.– Москва : ФОРУМ, 2008. – 240 с. – [Допущено МО РФ].
Пехлецкий, И. Д. Математика [Текст] : учеб. для студентов образовательных учреждений сред. проф. образования / И. Д. Пехлецкий,
– 6-е изд., стер. – Москва : ИЦ «Академия», 2010. – 304 с. – [Допущено МО РФ].
Периодические издания (отечественные журналы):
Математика [Текст] : методический журнал для учителей математики / учредитель ООО «Чистые пруды». - . - Москва : ИД «Первое сентября», 2008 - . - Ежемес. - [http://mat.lseptember.ru/].
Научные исследования в образовании [Текст] : приложение к журналу «Профессиональное образование. Столица» / учредители Департамент образования города Москвы; Российская академия образования; Академия профессионального образования. – 2006 – . – Москва : НИИРПО, 2008 – . – Ежемес.
Образование. Карьера. Общество [Текст] : учредитель ГОУ «Кузбасский региональный институт развития профессионального образования». – 2005 -.- Кемерово : ГОУ « КРИРПО», 2008 -.- Ежеквар. - [http://www.krirpo.ru/].
Профессиональное образование. Столица [Текст] : информационно-педагогическое, научно-методическое издание / учредители Департамент образования города Москвы; Российская академия образования; Академия профессионального образования. – 1997 – . – Москва : НИИРПО, 2008 – . – Ежемес. [http://www.e-profobr.ru/].
Интернет-ресурсы:
Вся математика в одном месте – математический портал [Электронный ресурс]. - Режим доступа : http://www.allmath.ru, свободный. - Загл. с экрана. – (Дата обращения: 27.08.2013).
Математика: справочник формул по алгебре и геометрии, решения задач и примеров. Математические формулы on-line [Электронный ресурс]. - Режим доступа : http://www.pm298.ru, свободный. - Загл. с экрана. - (Дата обращения: 27.08.2013).
Математика в нашем колледже [Электронный ресурс]. - Режим доступа : http://www.kptc.org/mathematic/index.html, свободный. - Загл. с экрана. - (Дата обращения: 27.08.2013).
Форум - математический сайт allmatematika.ru [Электронный ресурс]. - Режим доступа : http://www. allmatematika.ru, свободный. - Загл. с экрана. - (Дата обращения: 27.08.2013).
Электронно-библиотечная система издательства «Лань» [Электронный ресурс]. - Режим доступа : http://lanbook.com/ebs.php, для доступа к информ. ресурсам требуется авторизация. - Загл. с экрана.- (Дата обращения: 27.08.2013).
Электронно-библиотечная система «КнигаФонд» [Электронный ресурс]. - Режим доступа: http://www.knigafund.ru/, для доступа к информ. ресурсам требуется авторизация. - Загл. с экрана. - (Дата обращения: 27.08.2013

 Получите свидетельство
Получите свидетельство Вход
Вход



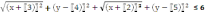
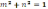
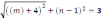
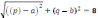
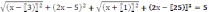
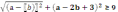

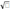
 1.Решим систему неравенств:
1.Решим систему неравенств: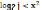
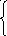 х2 +у2≤ 9, х2 +у2 ≤ 9,
х2 +у2≤ 9, х2 +у2 ≤ 9,








 Геометрическая и алгебраическая интерпретация математических понятий (1.11 MB)
Геометрическая и алгебраическая интерпретация математических понятий (1.11 MB)
 0
0 2895
2895 103
103 Нравится
0
Нравится
0


