Решение тригонометрических уравнений

Учиться можно только

весело…

Чтобы переваривать

знания, надо поглощать

их с аппетитом.

Анатоль Франс

1844 - 1924

Решение тригонометрических уравнений.

1 уравнения sin x = a при ‌ а ‌ 1 2 . При каком значении а При каком значении а уравнение sin x = a имеет решение? уравнение cos x = a имеет решение? Какой формулой Какой формулой выражается это решение? выражается это решение? 4. На какой оси откладывается значение а при решении уравнения cos x = a ? 4. На какой оси откладывается значение а при решении уравнения sin x = a ? " width="640"

Проверочная работа.

Вариант 1.

Вариант 2.

• Каково будет решение

• Каково будет решение

уравнения cos x = a при ‌ а ‌ 1

уравнения sin x = a при ‌ а ‌ 1

2 . При каком значении а

• При каком значении а

уравнение sin x = a имеет

решение?

уравнение cos x = a имеет

решение?

• Какой формулой

• Какой формулой

выражается это решение?

выражается это решение?

4.

На какой оси откладывается

значение а при решении

уравнения cos x = a ?

4.

На какой оси откладывается

значение а при решении

уравнения sin x = a ?

Проверочная работа.

Вариант 1.

Вариант 2.

5. В каком промежутке

находится arccos a ?

5 . В каком промежутке

находится arcsin a ?

• В каком промежутке

6. В каком промежутке

находится значение а?

находится значение а?

• Каким будет решение

7. Каким будет решение

уравнения sin x = 1?

уравнения cos x = 1?

8 . Каким будет решение

уравнения cos x = -1?

8. Каким будет решение

уравнения sin x = -1?

Проверочная работа.

Вариант 1.

Вариант 2.

9. Каким будет решение

уравнения cos x = 0?

9. Каким будет решение

уравнения sin x = 0 ?

• Чему равняется

10. Чему равняется

arcsin ( - a)?

arccos ( - a)?

• В каком промежутке

11. В каком промежутке

находится arcctg a?

находится arctg a?

• Какой формулой

12. Какой формулой

выражается решение

уравнения с tg x = а?

выражается решение

уравнения tg x = а?

№

Вариант 1.

1.

Вариант 2.

Нет решения

2.

Нет решения

3.

4.

5.

На оси Ох

На оси Оу

6.

7.

8.

9.

10.

11.

12.

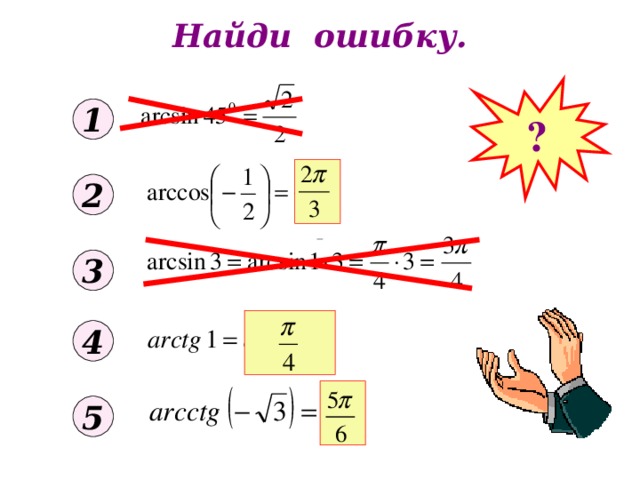
Найди ошибку.

?

1

2

3

4

5

Установите соответствие:

sin x = 0

1

cos x = -1

2

3

sin x = 1

cos x = 1

4

tg x = 1

5

sin x = - 1

6

7

cos x = 0

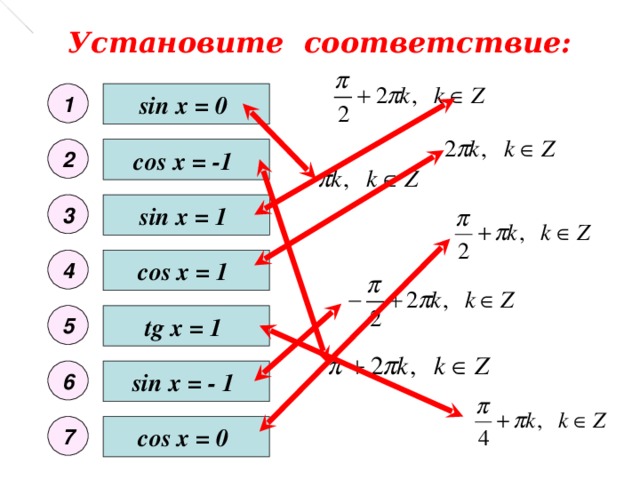
Установите соответствие:

1

sin x = 0

cos x = -1

2

sin x = 1

3

4

cos x = 1

5

tg x = 1

6

sin x = - 1

7

cos x = 0

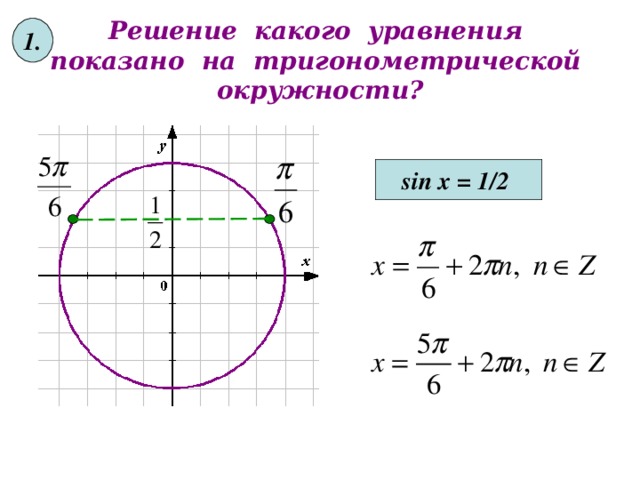
1.

Решение какого уравнения показано на тригонометрической окружности?

sin x = 1/2

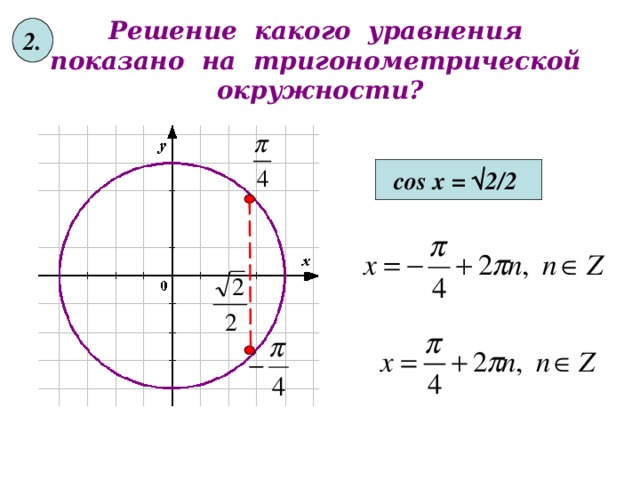
2.

Решение какого уравнения показано на тригонометрической окружности?

cos x = √ 2 /2

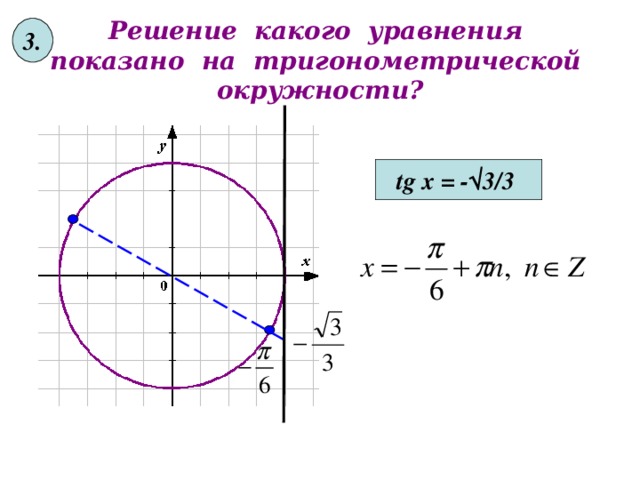
3 .

Решение какого уравнения показано на тригонометрической окружности?

tg x = - √ 3 / 3

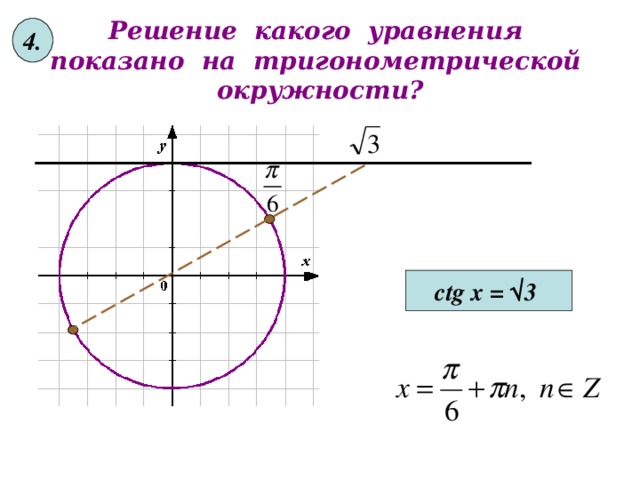
4 .

Решение какого уравнения показано на тригонометрической окружности?

ctg x = √ 3

Необходимо выбрать соответствующий прием для решения уравнений.

Методы решения тригонометрических уравнений.

Уравнения сводимые

к алгебраическим.

Вариант 1:

Вариант 2:

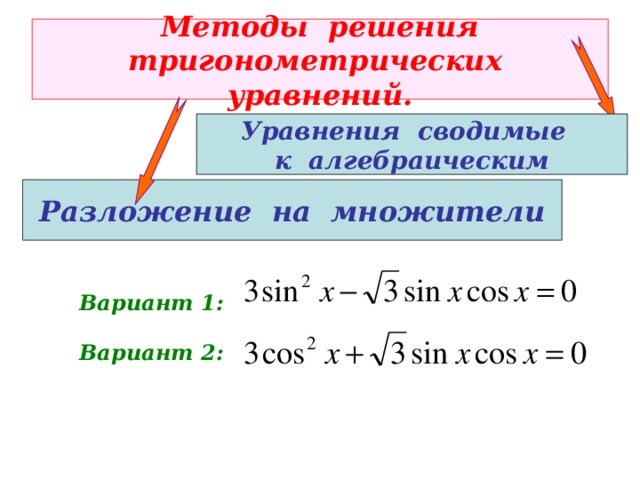
Методы решения тригонометрических уравнений.

Уравнения сводимые

к алгебраическим

Разложение на множители

Вариант 1:

Вариант 2:

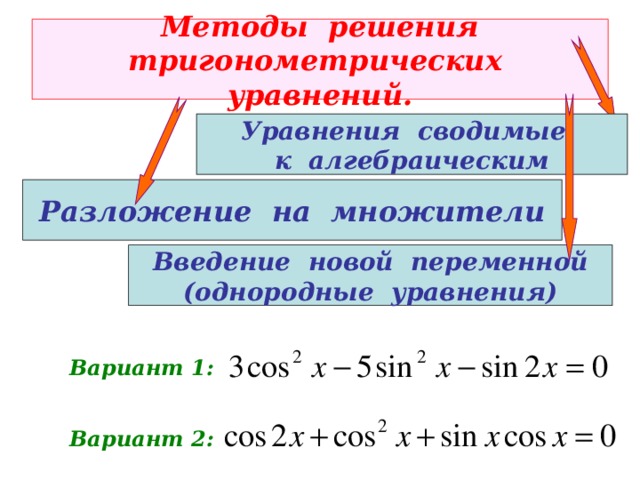
Методы решения тригонометрических уравнений.

Уравнения сводимые

к алгебраическим

Разложение на множители

Введение новой переменной

(однородные уравнения)

Вариант 1:

Вариант 2:

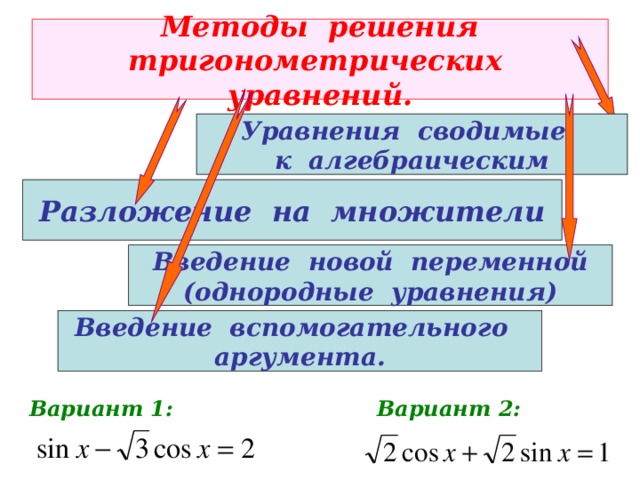
Методы решения тригонометрических уравнений.

Уравнения сводимые

к алгебраическим

Разложение на множители

Введение новой переменной

(однородные уравнения)

Введение вспомогательного

аргумента.

Вариант 2:

Вариант 1:

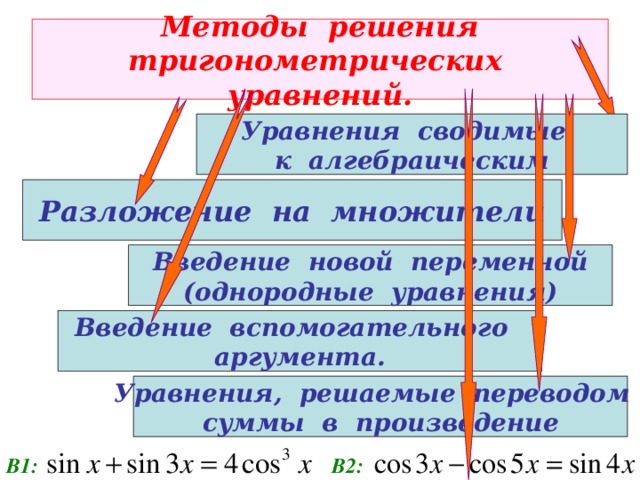
Методы решения тригонометрических уравнений.

Уравнения сводимые

к алгебраическим

Разложение на множители

Введение новой переменной

(однородные уравнения)

Введение вспомогательного

аргумента.

Уравнения, решаемые переводом

суммы в произведение

В1:

В2:

Применение формул понижения

степени.

Формулы квадрата половинных углов:

Формулы понижения степени:

2 sin 2 x + cos 4x = 0

В1:

В2: