Автор: преподаватель математики Сагитова Л. М.
Тема урока: «Решение рациональных неравенств методом интервалов»
Цели: Закрепить и проверить навыки решения рациональных неравенств высших степеней методом интервалов.
Образовательная:
1) формировать представления о социальных, культурных и исторических факторах становления математики;
2) формировать основы логического, алгоритмического и математического мышления;
3) формировать умения применять полученные знания при решении различных задач;
4) научиться решать рациональные неравенства методом интервалов;
5) формирование навыка вычисления значений функции в точке;
6) формирование навыка построения графика на компьютере при решении задач.
Развивающая: Выработать умение выделять главное, сравнивать, обобщать..
1)формирование умения самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность;
2) Формировать графическую культуру обучающихся, развитие логического мышления, навыков сравнительного анализа
3) формирование навыков познавательной, учебно-исследовательской деятельности, навыков разрешения проблем; способности и готовности к самостоятельному поиску методов решения практических задач;
4) формирование умения использовать средства информационных и коммуникационных технологий в решении задач;
5)формировать умение ясно, логично и точно излагать свою точку зрения.
Воспитательная:
1)Показать взаимосвязь математики с окружающей действительностью.
2) формирование представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
3)Формировать навыки общения, диалога, умение работать в коллективе, воспитание самостоятельности, творческого подхода к решению задач.
4) формирование основ саморазвития, самовоспитания, готовности и способности к самостоятельной, творческой и ответственной деятельности;
5) формирование гибкости мышления, инициативы, активности.
Оборудование: доска, компьютер, проектор, экран, записи на доске, карточки-задания.
Использование элементов педагогических технологий:
1. сотрудничества;
2. здоровьесберегающих (чередование видов деятельности);
3. информационно-коммуникационных;
4. развивающих;
5. личностно-ориентированных.
Формирование компетенций: учебно-познавательной, коммуникативной, ценностно-смысловой, личного самосовершенствования.
Тип урока: урок освоения новых знаний.
Форма урока: комбинированный.
Методы обучения: Частично-поисковый, диалоговый
Содержание урока:
I.Организационный момент:
Проверка посещаемости.
Проверка работы дежурных.
Проверка готовности группы к уроку.
II. Повторение пройденного на прошлом уроке.
1)Вопрос: Какие функции называются рациональными, дробно-рациональными?
Ответ: Неравенство вида 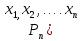 )
) 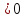 где
где 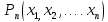 – многочлен называется рациональным.
– многочлен называется рациональным.
Неравенство вида 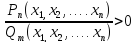 , где
, где 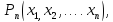
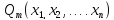 – многочлены называется дробно-рациональным.
– многочлены называется дробно-рациональным.
2)Вопрос: Что значит решит неравенство?
Ответ: Решить неравенство – значит найти множество всех х, для которых данное неравенство выполняется.
3)Вопрос: Какие неравенства называются равносильными?
Ответ: Два неравенства называются равносильными, если множества решений их совпадают, т.е. если всякое решение каждого из них является решением другого.
4)Перечислите способы решения неравенств.
Разложение на системы неравенств;
Графический способ;
Метод интервалов.
5)Решение квадратных неравенств графическим способом.
3х2 -7х -5
Найдем нули функции f (x) = 3х2 -7х -5,
то есть решим уравнение 3х2 -7х -5 =0
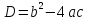 = (-7)2 -4·3·(-5) = 49+60=109
= (-7)2 -4·3·(-5) = 49+60=109
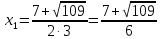 ,
, 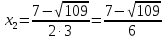
Два корня, значит, парабола ветвями, направленными вверх, пересекает ось в двух точках.

 + + х
+ + х
 -
- 
При пересечении параболы с осью четко виден промежуток, где функция принимает отрицательные значения. На остальных двух промежутках функция принимает положительные значения. Выписываем решение х  (
(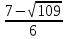 ;
;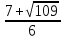 )
)
Ответ: (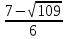 ;
;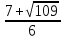 )
)
III. Объяснение нового материала.
1.Решить неравенство 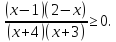
Функция f(x) = 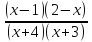 непрерывна в каждой точке своей области определения ( это дробно-рациональная функция) и обращается в ноль в точках 1 и 2. Область определения - вся числовая ось, за исключением нулей знаменателя, то есть точек х = - 4 и х = -3.Эти точки и точки х = 1 и х = 2 разбивают числовую ось на пять промежутков. В каждом из этих промежутков функция непрерывна и не обращается в ноль. Проверим знаки функции в каждом из промежутков, вычислив значение функции во внутренних точках каждого интервала.
непрерывна в каждой точке своей области определения ( это дробно-рациональная функция) и обращается в ноль в точках 1 и 2. Область определения - вся числовая ось, за исключением нулей знаменателя, то есть точек х = - 4 и х = -3.Эти точки и точки х = 1 и х = 2 разбивают числовую ось на пять промежутков. В каждом из этих промежутков функция непрерывна и не обращается в ноль. Проверим знаки функции в каждом из промежутков, вычислив значение функции во внутренних точках каждого интервала.
f(-5) = 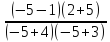 =
=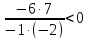
f(-3,5) = 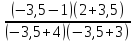 =
=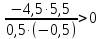
f(0) = =
f(1,5) = =
f(3) = =
+ - + - х
-4 -3 1 2
Неравенство нестрогое , поэтому точки 1 и 2 являются решением неравенства. Решением неравенства являются промежутки, где функция f принимает положительные значения либо 0.
Ответ: (-4;-3).
2.Решить неравенство (1)
Неравенство (1) строгое, можно заменить его равносильным неравенством (2)
(х-1) (2)
Найдем все точки, делящие числовую ось на промежутки. Это
точки 1, 3, -5, 4.
х
-5 1 3 4
Выражения ( принимают положительные значения при любом х, и не влияют на знак (2). Следовательно, неравенство (2) можно заменить равносильным (3)
(х-1) (3).
Проверим знаки неравенства в каждом из промежутков, вычислив значения во внутренних точках интервалов.
f(-6) = (-6-1)
f(0) = (0-1)
f(2) = (2 -1)
f(3.5) = (3.5 -1)
f(5) = (5 -1)
- + - - + х
-5 1 3 4
Ответ:
IV.Закрепление нового материала: Продолжаем решать неравенства. К доске вызываются двое обучающихся. Преподаватель направляет их деятельность.
3.Решить неравенство: (2х-3) (1).
Найдем нули функции f (x) = (2х-3)
| 1)2x-3=0 x = 1,5
| D=
| 3) 4 D=
|
х
1- 0,5 1,5 1-
Для удобства определения знака значения функций в каждом из получившихся интервалов, воспользуемся теоремой Виета
f (x) = 2(х-1,5) или
f (x) = 2 (2)
Проверим знаки функции (2) в каждом из промежутков, вычислив значение функции во внутренних точках каждого интервала.
f (-2) = 2
f (0) = 2
f (1) = 2
f (2) = 2
f (3) = 2
Ответ: ( +
4.Решить неравенство (1)
для любых х и влияния на знак выражения не оказывает.
Найдем нули функции f (x) = - Для этого решим уравнение
-
,
Т.к. как D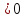 . Корней уравнения нет. Парабола f (x) = -
. Корней уравнения нет. Парабола f (x) = - не пересекает ось, ветви параболы направлены вниз.
х
Это значит - для любых х, то есть выражение
(- можно представлять как отрицательное число.
Неравенство (1) заменим равносильным неравенством (2).
или
(2)
Найдем все точки, делящие числовую ось на промежутки. Это
точки -2, -4, 3, 8.
-4 -2 3 8
Проверим знаки неравенства в каждом из промежутков, вычислив значения во внутренних точках интервалов.
f (-5) =
f (-3) =
f (0) =
f (4) =
f (9) =
- + + - +
-4 -2 3 8
Выпишем решение х (-4;-2)
Ответ: (-4;-2)
V. Подводятся итоги урока: 1)Выставление оценок.
2)Комментирование работы обучающихся.
3)Рефлексия в форме диалога:
Рефлексия
| 1 | ||
| На уроке я работал | активно | пассивно |
| 2 | ||
| Я не достиг хорошего результата | потому, что … | потому, что … |
| 3 | ||
| Материал урока мне был | понятен | не понятен |
VI. Домашнее задание: Учебное пособие. Задачник. М.И. Башмаков Математика Алгебра и начала анализа, геометрия
Стр.290, № 12.8 А (1-5)
Приложение 1
Указать пары равносильных неравенств
| Неравенства | | 6x-3 | - 4x+2 | | ln(2x) |
| 2х-1 |
|
|
|
|
|
| 1-2х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Решение рациональных неравенств методом интервалов (168.45 KB)
Решение рациональных неравенств методом интервалов (168.45 KB)
 0
0 112
112 0
0 Нравится
0
Нравится
0


