Получите свидетельство
Вход
Тема урока : « Решение логарифмических неравенств введением вспомогательной переменной» .
ОПРЕДЕЛЕНИЕ
Неравенства, которые содержат переменную под знаком логарифма или в его основании, называются логарифмическими.
Решение логарифмических неравенств основано на строгой монотонности логарифмической функции. Известно, что
при основании, большем единицы (a1), логарифмическая функция возрастает (т.е. большему значению аргумента соответствует большее значение функции,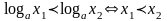 
).
при положительном основании, меньшем единицы(0a, логарифмическая функция убывает (т.е. большему значению аргумента соответствует меньшее значение функции,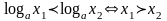 
).
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
Теорема: Если f(x) 0 и g(x) 0, то:
при a 1 логарифмическое неравенство log a f(x) log a g(x) равносильно неравенству того же смысла: f(x) g(x);
при 0 a a f(x) log a g(x) равносильно неравенству противоположного смысла: f(x) g(x).
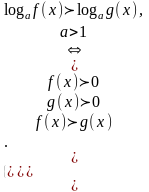и 
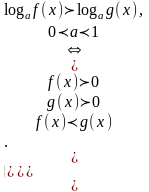
Решение простейших логарифмических неравенств мы рассматривали на прошлой лекции, сегодня еще один подход к решению логарифмических неравенств.
Некоторые логарифмические неравенства можно решить методом замены переменной. Рассмотрим несколько примеров на применение данного метода:
Пример 1: Решить неравенство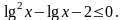
Решение : ОДЗ: х0
Введем замену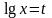 
, тогда получим неравенство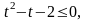
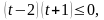
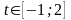или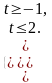
Сделаем обратную замену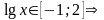 
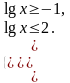
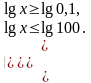, т.к. основание логарифма 101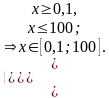 
Ответ: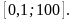 
Пример 2: Решить неравенство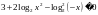 
Решение:
ОДЗ: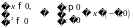 
К первому логарифму в левой части неравенства применим свойство логарифма степени: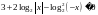 
С учетом ОДЗ, получим: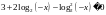 
Введем замену 
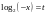, тогда получим неравенство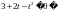
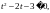
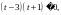
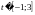или
Делаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются и получаем систему:
Пересечение с ОДЗ дает этот же промежуток.
Ответ: 
Пример 3: Решить неравенство 
Решение:
ОДЗ:
Введем замену 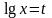, тогда неравенство примет вид: 
Перенесем все влево и сведем к общему знаменателю: 
Получим 
Делаем обратную замену и возвращаемся к первоначальной переменной 
:
Так как основание логарифмов больше 1, то знаки неравенств сохраняются и получаем: 
Пересекая с ОДЗ, окончательно имеем: 
.
Ответ: 
Пример 4: Решить неравенство
Решение:
ОДЗ: 
Используя свойство логарифма степени и формулы замены основания, приведем второй логарифм к основанию 3
Введем замену 
, тогда неравенство примет вид: 
при любом значении t, так как дискриминант квадратного трехчлена 
.
Следовательно
Перейдем к х, для этого делаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются. Пересекая с ОДЗ, окончательно имеем промежуток: 
.
Ответ: 
Пример 5: Решить неравенство
Решение:
ОДЗ:
Используя формулы замены основания, приведем все логарифмы в рассматриваемом неравенстве к логарифмам по основанию 2:
Распишем полученные логарифмы, используя свойство суммы логарифмов:
В ведем замену 
, тогда неравенство примет вид: 
Имеем
Сделаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 
То есть
С учетом ОДЗ, окончательно имеем:
Ответ: 
Пример 6: Решите неравенство
Решение:
ОДЗ:
Используя формулы замены основания, приведем все логарифмы в рассматриваемом неравенстве к логарифмам по основанию 3:
В ведем замену , тогда неравенство примет вид: 
Имеем 
Сделаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 
С учетом ОДЗ, окончательно имеем: 
Ответ: 
Пример 7: Решите неравенство 
Решение:
ОДЗ: 
В ведем замену , тогда неравенство примет вид: 
Имеем 
Сделаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 
С учетом ОДЗ, окончательно имеем: 
Ответ: 
Пример 8: Решите неравенство 
Решение:
ОДЗ:
В ведем замену 
, тогда неравенство примет вид: 
Имеем 
Сделаем обратную замену: 
Так как основание логарифмов больше 1, то знаки неравенств сохраняются: 
С учетом ОДЗ, окончательно имеем:
Ответ:
Решение логарифмических неравенств. (273.36 KB)
0
122
19
Нравится
0
