Цели урока:
- Формировать умение решать тригонометрические уравнения методом мажоранта;
- Воспитание мотивов учения, положительного отношения к знаниям через знакомство с исторической справкой;
- Развивать у ребят умение самостоятельно выполнять задания, умение работать с учебным материалом, контролировать свою деятельность, адекватно оценивать результаты своей деятельности.
Формы работы учащихся: фронтальная, индивидуальная.
Оборудование: учебник «Алгебра 10-11» УМК А.Н.Колмогорова; доска; таблицы корней простейших тригонометрических уравнений и значений тригонометрических функций; карточки для индивидуальной работы учащихся; таблица ответов для проверки индивидуальных заданий, портреты ученых, ноутбук, мультимедийный проектор, презентация.
Ход урока
Оргмомент (приветствие)
Актуализация знаний учащихся, полученных ими по теме «решение простейших тригонометрических уравнения»
Устная работа (см. на слайды)
- повторим формулы корней простейших тригонометрических уравнений. - смотри документ
-Существуют разные версии возникновения тригонометрических терминов. При выполнении задания по карточкам вы соберете пазл и узнаете кому по одной из версий пошли термины «синус» и «косинус». А вторая группа узнает и поделиться кто является предполагаемым автором первых тригонометрических таблиц.(приложение № 1, № 2 ,рисунок разрезается на 6 частей, учащиеся собирают мозаику по мере решения уравнений )
1 вариант
1) 2 cos ²x-cosx-1=0
2) 2 cos ²x+2sinx=2,5
3) √3 tg²x-3 tgx=0
4) sinx=-√3 cosx
5) sin²x-4 sinx cosx+3 cos²x=0
6) cos x=0
2 вариант
1) 6 cos ²x+cosx-1=0
2) 5 cos ²x+6sinx=6
3) 3 tg²x-2 tgx=0
4) sinx= cosx
5) 3sin²x+ sinx cosx-2 cos²x=0
6) sin x=0
Ответы - смотри документ.
(После выполнения задания версии и озвучивает имя автора первых тригонометрических таблиц)
- Решение простейших уравнений мы вспомнили, можно приступать к решению более сложных уравнений.
Вспомним, какие методы тригонометрических уравнений мы знаем.
Наверное, надо начать с общих методов, какие общие методы вы знаете?
-А какие методы относятся к специальным?
-Перед каждым учеником лежит лист, на котором записано 10 уравнений, необходимо определить каким методом необходимо решить то или иное уравнение
- Внимательно посмотрите на уравнение №8.
Можете ли вы сейчас предложить метод его решения? В чем заключается проблема его решения?
- Такие уравнения решаются особым методом - “Методом мажорант”, с которым вас познакомит ваш одноклассник.
Выступление ученика по теме “Метод мажорант”.
- Посмотрите, какие еще уравнения можно решить этим же методом?
Задания - смотри документ
ИТОГ урока:
Показываем слайд с 10 уравнениями и просим выбрать те, которые решаются с помощью метода Мажоранта.
-Суть этого метода?
-Алгоритм решения?
Д/задание.

 Получите свидетельство
Получите свидетельство Вход
Вход


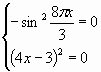









 Решение тригонометрических уравнений (0.1 MB)
Решение тригонометрических уравнений (0.1 MB)
 0
0 666
666 51
51 Нравится
0
Нравится
0


