Решение неравенств второй степени с одной переменной

Цели: Организовать восприятие, осмысление и первичное запоминание способов решения неравенств  второй степени с одной переменной.

Задачи:

- научить решать неравенства второй степени с одной переменной;

- развивать математическую речь учащихся, мышление, вычислительные навыки;

- воспитывать усидчивость, трудолюбие.

Ход урока.

1. Организационный момент

Приветствие. Выявление отсутствующих.

2. Актуализация опорных знаний

Учащиеся выполняют тест на повторение в двух вариантах - смотри архив.

3. Изучение нового материала.

Определение: Неравенства вида ax²+bx+c>0 и ax²+bx+c<0, где х - переменная, a, b, c – числа, причем а ¹ 0 называется  квадратным.

Алгоритм решения квадратных неравенств.

1. Ввести функцию у = ax²+bx+c и выяснить направление ветвей параболы (а > 0 – вверх, а < 0 - вниз).
2. Приравнять функцию к нулю и найти корни квадратного уравнения.
3. Отметить полученные корни на числовой прямой.
4. Построить эскиз графика функции, учитывая направление ветвей параболы.
5. Определить промежутки в которых парабола выше оси Ох или ниже, в зависимости от знака неравенства.
6. Записать ответ, учитывая знак неравенства.

Для выполнения пунктов 5 и 6 можно воспользоваться следующей таблицей. Таблица заполняется совместно с учащимися на доске.

ax²+bx+c>0

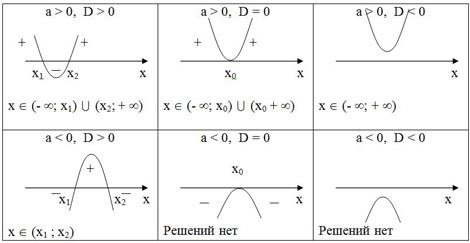
ax²+bx+c<0

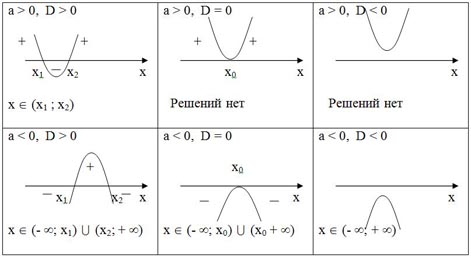
Рассмотреть примеры.

Пример 1.

Решить неравенство 5х² + 9х – 2 < 0

Пример 2.

Решить неравенство 3х² - 11х – 4 > 0

Пример 3.

Решить неравенство -1/4х² + 2х – 4 < 0

Пример 4.

Решить неравенство х² - 3х + 4 > 0

5. Домашнее задание (по учебнику)

6. Подведение итогов