Решение квадратных уравнений

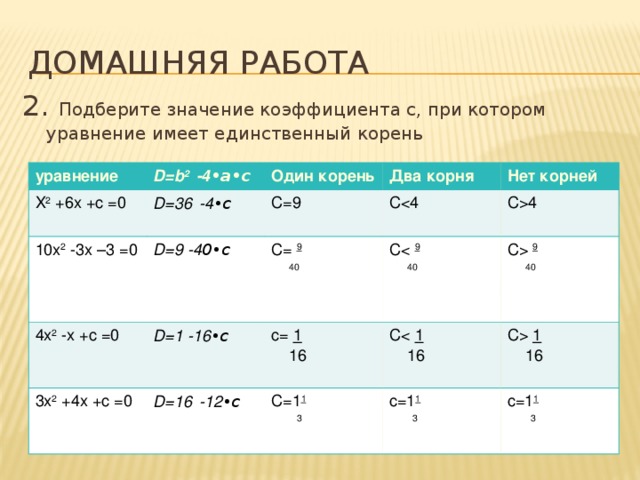
Домашняя работа

2. Подберите значение коэффициента с, при котором уравнение имеет единственный корень

уравнение

D=b 2 -4 •a•c

X 2 +6х +с =0

D=36 -4 •c

Один корень

10х 2 -3х –3 =0

D=9 -4 0•c

Два корня

4х 2 -х +с =0

С=9

С

D=1 -16 •c

Нет корней

C= 9

3х 2 +4х +с =0

D=16 -12 •c

C9

40

c= 1

C4

40

C=1 1

C1

16

C 9

40

16

3

c=1 1

C 1

3

16

c=1 1

3

Вопросы теста

• Запишите общий вид квадратного уравнения

Уравнение вида а х 2 +bх+с=0

2. Запишите формулу дискриминанта квадратного уравнения

D=b 2 - 4 •a•c

0 ( 2 корня ) D=0 (1 корень) DX 2 = X 1 = " width="640"

Вопросы теста

3. Напишите формулу корней квадратного уравнения

4. Сколько корней может иметь квадратное уравнение в зависимости от дискриминанта?

D0 ( 2 корня ) D=0 (1 корень) D

X 2 =

X 1 =

Вопросы теста

5. Напишите формулу корней квадратного уравнения, в котором второй коэффициент четное число

D 1 =k 2 - ac

x 1 =

x 2 =

0 и D=0 D0 X 1 = X 2 = D=0 X = " width="640"

Вопросы теста

6. По какой формуле вычисляют корни квадратного уравнения при D0 и D=0

D0

X 1 = X 2 =

D=0

X =

Вопросы теста

7. Запишите коэффициенты квадратного уравнения: 2х 2 - 6х -14=0

a = 2 b=-6 c=-14

8 . Решите уравнение:х 2 - 11х +18=0

D=121-4•1 •18=121-72=49

X 1 = 2 x 2 =9

Самостоятельная работа

• 1 вариант

• 2 вариант

• (х+3) 2 =2х+6

• (х+2) 2 =43-6х

• (х-3)(х+3)=5х-13

• (х-2)(х+2)=-5х-10

• х 2 -11 = х- х 2

• 2х 2 +х = 4х-2

5 3

7 2

0(2 k) х 1 = x 2 = x 1 =3 x 2 =-13 х 2 +6х+9-2х-6=0 х 2 +4х+3=0 D=4 2 -4 • 1 •3=40(2 k) x 1 = х 2 = x 1 =-1 х 2 =-3 " width="640"

Решение задания №1

х 2 +4x+4-43+6x=0

х 2 +10x-39=0

D=10 2 -4 •1 •(-39)=2560(2 k)

х 1 =

x 2 =

x 1 =3

x 2 =-13

х 2 +6х+9-2х-6=0

х 2 +4х+3=0

D=4 2 -4 • 1 •3=40(2 k)

x 1 =

х 2 =

x 1 =-1

х 2 =-3

Решение задания №2

х 2 -4=-5х-10

Х 2 -9=5х-13

х 2 -9-5х+13=0

х 2 -4+5х+10=0

х 2 +5х+6=0

х 2 -5х+4=0

D=25-4•1 •4=25-16=9

D=25-4•1 •6=25-24=1

X 1 =

X 1 =

Х 2 =

Х 2 =

x 1 =-2

x 1 =4

х 2 =-3

х 2 =1

Решение задания №3

3 • (2х 2 +х)=5 • (4х-2)

6х 2 +3х=20х-10

6х 2 +3х-20х+10=0

6х 2 -17х+10=0

D=289-4•10 •6=49

х 1 =

Х 2 =

x 1 =2

х 2 =

2 • (х 2 -11)=7 • (х-х 2 )

2 х 2 -22=7 х-7х 2

2 х 2 -22-7 х+7х 2 =0

9 х 2 -7 х-22=0

D=49-4•9 •(-22)=841

х 1 =

Х 2 =

x 1 =2

х 2 =-