Решение комбинаторных задач

В презентации из 14 слайдов представленны:

- кроссворды;
- задания на комбинаторику;
- правило умножения;
- различные задачи с решениями или ответами;
- рефлексия.

Учитель математики МОУ СОШ № 20 Суворова Л.В.

п. Железнодорожный

2010 год

ГЛ = К

КОМБ

ИНАТОР

ИКА

Комбинаторика – это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям.

Здесь изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Латинское слово combinare означает «соединять, сочетать».

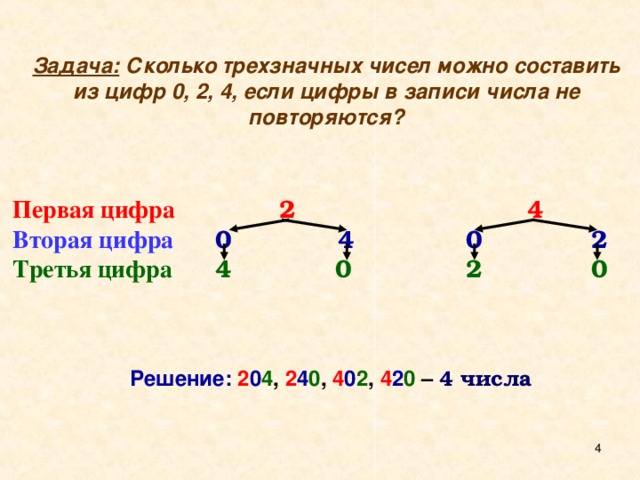
Задача: Сколько трехзначных чисел можно составить из цифр 0, 2, 4, если цифры в записи числа не повторяются?

Первая цифра 2 4

Вторая цифра 0 4 0 2

Третья цифра 4 0 2 0

Решение: 2 0 4 , 2 4 0 , 4 0 2 , 4 2 0 – 4 числа

Задача 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 7?

10

12

20

14

22

40

50

24

42

70

44

52

54

72

74

0

2

4

1

2

4

5

7

Решение:

Первые цифры искомых чисел: 1, 2, 4, 5, 7, второй цифрой искомых чисел могут быть: 0, 2. 4.

5 · 3 = 15 двузначных чисел

Задача 2. В школьной столовой на завтрак любой ученик может выбрать булочку, ватрушку или пирожок, а запить их можно соком или чаем. Сколько вариантов завтрака предлагается в школьной столовой?

Булочка (Б)

Ватрушка (В)

Пирожок (П)

СБ

СВ

ЧБ

СП

ЧВ

ЧП

Сок (С)

Чай (Ч)

Решение: 3 · 2 = 6 вариантов завтрака

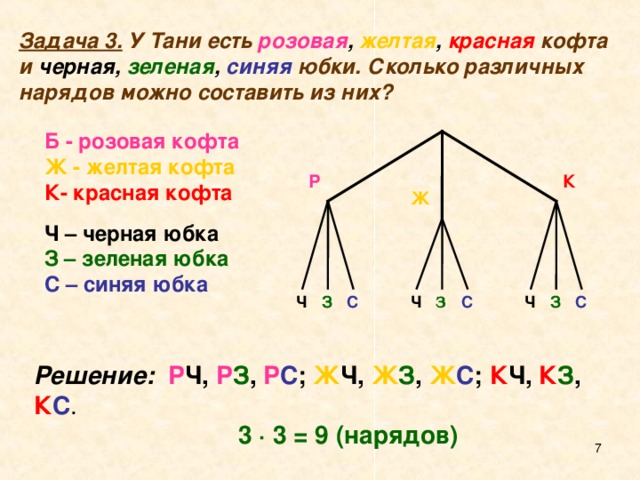
Задача 3. У Тани есть розовая , желтая , красная кофта и черная, зеленая , синяя юбки. Сколько различных нарядов можно составить из них?

Б - розовая кофта

Ж - желтая кофта

К- красная кофта

Ч – черная юбка

З – зеленая юбка

С – синяя юбка

К

Р

Ж

С

Ч

З

Ч

З

С

С

Ч

З

Решение: Р Ч, Р З , Р С ; Ж Ч, Ж З , Ж С ; К Ч, К З , К С .

3 · 3 = 9 (нарядов)

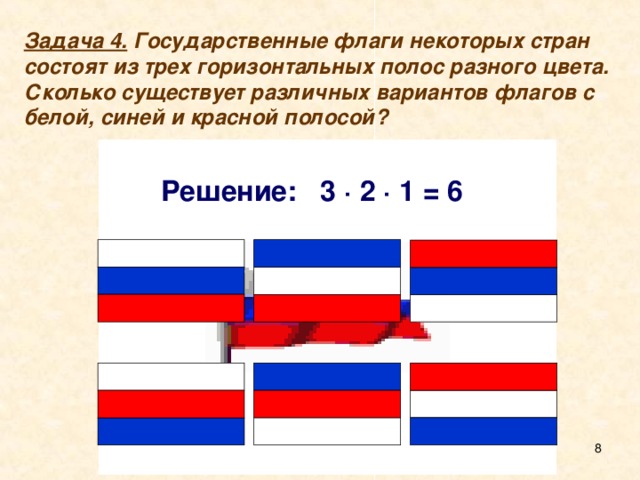
Задача 4. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?

Решение: 3 ∙ 2 ∙ 1 = 6

7

Правило умножения:

Если объект a можно выбрать m способами, а объект b можно выбрать k способами, то выбор пары ( a , b ) можно осуществить

m · k способами.

8

Задачи:

1. Мастер должен обшить 12 стульев обшивкой красного, коричневого и зеленого цвета. Сколькими способами он может это сделать?

Ответ: 12 ∙ 3 = 36

2. Сколькими способами можно выбрать гласную и согласную буквы из слова «правило»?

Ответ: 3 ∙ 4 = 12

3. На первой полке стоит 5 книг, а на второй 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй?

Ответ: 5 ∙ 10 = 50

4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Ответ: 9 ∙ 10 ∙ 10 = 900

8

РЕШЕНИЕ:

№ 53

№ 410

№ 517

№ 915

6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720 способов;

2 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 240 способов

10 ∙ 9 ∙ 8 ∙ 7 = 1540 номеров

25 ∙ 24 = 600 способов

27; 57; 87; 387; 357; 537; 837

8

5

1

8

Домашнее задание :

№ 24, № 262, № 355, № 462

Математика повсюду – Глазом только поведешь И примеров сразу уйму Ты вокруг себя найдешь…

Составить комбинаторные задачи

практического содержания.

8

8