Решение иррациональных уравнений

В работе представлен теоретический материал по теме и его практическое применение при решении типовых примеров. А так же даны примеры для самостоятельного закрепления материала.

Уравнение, содержащее переменную под знаком корня,  называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения (иногда несколько раз)  или замены переменной.

При возведении обеих частей иррационального уравнения в четную степень возможно появление посторонних корней. Чтобы выявить «посторонние» корни, все найденные корни проверяют подстановкой в исходное уравнение и «посторонние» корни отбрасывают.

При возведении обеих частей иррационального уравнения в нечетную степень получается уравнение, равносильное исходному.

Тема : Иррациональные уравнения теоретический материал

Иррациональные уравнения

• Уравнение, содержащее переменную под знаком корня, называется иррациональным .

• Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения (иногда несколько раз) или замены переменной.

Иррациональные уравнения

• При возведении обеих частей иррационального уравнения в четную степень возможно появление посторонних корней. Чтобы выявить «посторонние» корни, все найденные корни проверяют подстановкой в исходное уравнение и «посторонние» корни отбрасывают.
• При возведении обеих частей иррационального уравнения в четную степень возможно появление посторонних корней. Чтобы выявить «посторонние» корни, все найденные корни проверяют подстановкой в исходное уравнение и «посторонние» корни отбрасывают.

• При возведении обеих частей иррационального уравнения в нечетную степень получается уравнение, равносильное исходному.
• При возведении обеих частей иррационального уравнения в нечетную степень получается уравнение, равносильное исходному.

Иррациональные уравнения

• Пример 1 . Решить уравнение:

Возведем обе части уравнения в квадрат:

Проверим найденные корни, подставив их в исходное уравнение.

Проверка: 1) 2)

Найденные корни удовлетворяют исходному уравнению.

Ответ:

Иррациональные уравнения

• Пример 2 . Решить уравнение:.

Возведем обе части уравнения в куб:

Ответ:

• Пример 3 . Решить уравнение: .

Возведем обе части уравнения в квадрат:

По теореме Виета:

Проверим найденные корни, подставив их в исходное уравнение.

Проверка: 1) 2)

корень

Ответ:

Иррациональные уравнения

• Пример 4 . Решить уравнение:.

Возведем обе части уравнения в квадрат:

Проверка:

– посторонний корень

Ответ: решений нет

Иррациональные уравнения

• Пример 5 . Решить уравнение:.

Уединим радикал в левой части:

Возведем обе части уравнения в квадрат:

По тереме Виета:

Проверим найденные корни, подставив их в исходное уравнение.

Проверка: 1) 2)

корень

Ответ:

Иррациональные уравнения

Задания для самостоятельного решения

• Не решая уравнений, объясните, почему каждое из них не может иметь корней:

• Решите уравнения.

Иррациональные уравнения

Домашнее задание

Решите уравнения:

Иррациональные уравнения

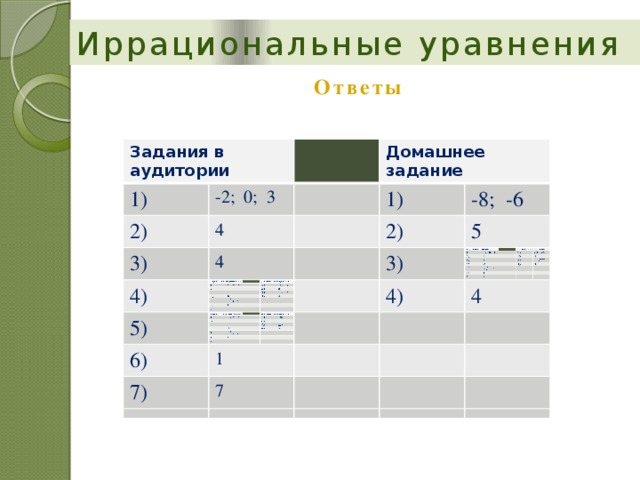
Ответы

Задания в аудитории

Задания в аудитории

1)

1)

-2; 0; 3

-2; 0; 3

2)

2)

Домашнее задание

4

4

Домашнее задание

3)

3)

1)

4)

4

4

1)

4)

2)

2)

5)

5)

-8; -6

-8; -6

5

6)

6)

3)

5

3)

1

4)

1

4)

7)

7)

4

4

7

7