Пояснительная записка
Данный элективный курс для профильной подготовки учащихся 11 классов. Проводиться во втором полугодии и включает некоторые методы решения иррациональных уравнений с помощью неравенств.
Новизна. В данной работе систематизирован теоретический и практический материал по применению классических неравенств в решении иррациональных уравнений.
Актуальность: помогает систематизировать материал для подготовки учащихся к ЕНТ и тем самым повысить результативность итогового балла по математике.
Цель курса: изучить ряд классических неравенств и уметь правильно их использовать при решении иррациональных уравнений.
Задачи курса:
1) Формирование представления о классических неравенствах имеющих важное значение как в алгебре, так и в геометрии;
2) Развитие логической и методологической культур;
3) Овладение общими приемами организации действий: планированием, осуществлением плана, анализом и выражением результатов действий.
Данный курс способствует подготовке учащихся к продолжению обучения в классах с углубленным изучением математики. Он расширяет базовый курс по алгебре, познакомит учащихся с нестандартными, интересными подходами при решении иррациональных уравнений.
Ожидаемые результаты и способы их проверки
Учащиеся должны знать и уметь:
- уметь применять изученный теоретический материал на практике;
- овладеть навыками решения иррациональных уравнений используя классические неравенства;
- систематизировать знания по решению данных уравнений.
Формы подведения итогов реализации программы – контрольная работа, с последующим анализом учителя.
В школьных учебниках по математике в главе « Степени и корни. Степенная функция» приведены задачи, решение которых позволяет учащимся усвоить свойства уравнений и неравенств, но не прибавляет им новых знаний, поэтому время, затраченное на решение задач, используется недостаточно эффективно.
В школьном курсе математики выделены четыре основных метода решения уравнений: разложение на множители, замена переменной, переход от равенства функций к равенству аргументов, функционально - графический.
Опыт показывает, что учащиеся в недостаточной степени овладевают умением решать иррациональные уравнения, часто допускают ошибки при их решении. Однако задачи по теме «Иррациональные уравнения» встречаются на вступительных экзаменах, и они довольно часто становятся «камнем преткновения»
При изучении неравенств можно углубить знания учащихся, если рассмотреть несколько популярных неравенств, которые можно доказать, опираясь на материал, не выходящий за рамки школьной программы. Как правило, они используются в том случае, когда уравнение весьма затруднительно решить основными методами.
Знания и умения использовать классические неравенства при решении данных уравнений, учащиеся могут использовать как собственно в теории неравенств, так и в приложениях, в математическом анализе, геометрии, алгебре.

Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход







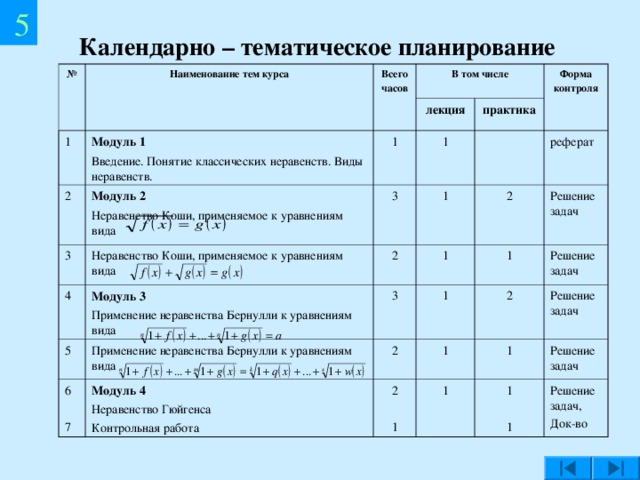

















 Элективный курс по математике "Применение классических неравенств в решении иррациональных уравнений" (0.3 MB)
Элективный курс по математике "Применение классических неравенств в решении иррациональных уравнений" (0.3 MB)
 0
0 684
684 15
15 Нравится
0
Нравится
0


