г. Брянск
конспект урока
на тему

Учитель математики и информатики
Киреева Мария Альгпимантасовна
Цели:
вспомнить способы разложения на множители: вынесение за скобки, с помощью формул сокращенного умножения и способа группировки;
ввести теорему о разложении квадратного трехчлена на множители и доказать ее;
отработать на примерах применение формулы;
создать условия для развития познавательного интереса к предмету, формирования логического мышления и самоконтроля при использовании разложения на множители.
Тип урока: урок изучения нового материала
Оборудование: проектор, презентация, карточки с цифрами 1, 2,3,4.
План:
Организационный момент. Сообщение темы, цели, задач урока и мотивация учебной деятельности (2 мин).
Актуализация знаний учащихся. (5 мин).
Изучение нового материала (15 мин).
Закрепление формулы на примерах (15 мин).
Проверочный самоконтроль (3 мин).
Подведение итогов урока (1 мин).
Постановка домашнего задания (1 мин).
Рефлексия. (0,5 мин).
Ход урока:
| Деятельность учителя | Деятельность ученика | |
| 1. Организационный момент | ||
|
| ||
| -Здравствуйте ребята. Сообщаем учащимся тему урока. -Как вы думаете, какие цели перед нами будут стоять? -Но вы это уже умеете. -Все верно. Наша основная задача: научиться правильно разлагать квадратный трехчлен на множители новым способом, с которым очень скоро мы познакомимся. | Учащиеся записывают дату и тему урока. -Научится раскладывать квадратный трехчлен на множители. -Значит, познакомимся с еще одним способом. | |
| Актуализация знаний учащихся | ||
| -Итак, вы уже ранее встречались с разложением многочлена на множители. Каким образом вы это делали?
-Выполните следующие задания (задания появляются на экране) 4х3-х2; а4-169а2; с3-8с2+16с; 3х2-21х+30.
-Что называется корнем квадратного трехчлена?
- Обратим внимание на 2 последних квадратных трехчлена. Вы можете назвать их корни? -Правильно. А чему равен старший коэффициент?
-Какой вывод можем сделать. После того как мы применили метод группировки, то получили квадратный трехчлен в виде … -Молодцы. Таким образом мы подошли к теореме о разложении квадратного трехчлена на множители(слайд№5).Запишем ее в тетрадь. | - Выносили общий множитель за скобки; -группировали; -пользовались формулами сокращенного умножения.
С места один из учеников комментирует, параллельно на экране появляется решение. 4х3-х2=х2(4х-1); а4-169а2= а2(а2-169)= а2(a-13)(a+13); с3-8с2+16с=c(с2-8с+16)=c(c-4)2; 3х2-21х+30=3(х2-7х+5)= 3(х2-2х-5x+5)=3(x(x-2)-5(x-2))=3(x-2)(x-5); 5х2-15х+10=5(х2-3х+2)=5(х2-х-2x+2) =5(x(x-1)-2(x-1))=5(x-1)(x-2).
- значение переменной, при которой данный квадратный трехчлен обращается в 0.
- Да, 2 и 5; 1 и 2. -
3; 5
-произведения старшего коэффициента на разность переменной с каждым из корней.
| |
| Усвоение теоремы: | ||
| -Что дано в теореме?
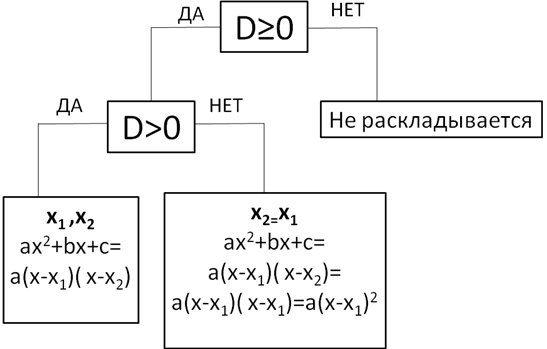
-Что требовалось доказать? -Какова полная формулировка? -То есть для того чтобы разложить квадратный трехчлен на множители нам необходимо сначала… -А потом? -Но ведь квадратный трехчлен не всегда имеет корни. Какие могут быть ситуации? -Все выше сказанное можно представить в виде блок-схемы.(слайд №7)
| -квадратный трехчлен ax2+bx+c и его корни х1 и х2 .
ax2+bx+c=a(x-x1)( x-x2)
Если х1 и х2 корни квадратного трехчлена ax2+bx+c, то ax2+bx+c=a(x-x1)( x-x2
-найти его корни
- подставить в формулу. -Он может иметь 1 корень(если D=0 ), а может вообще не иметь корней(если D
| |
| Закрепление | ||
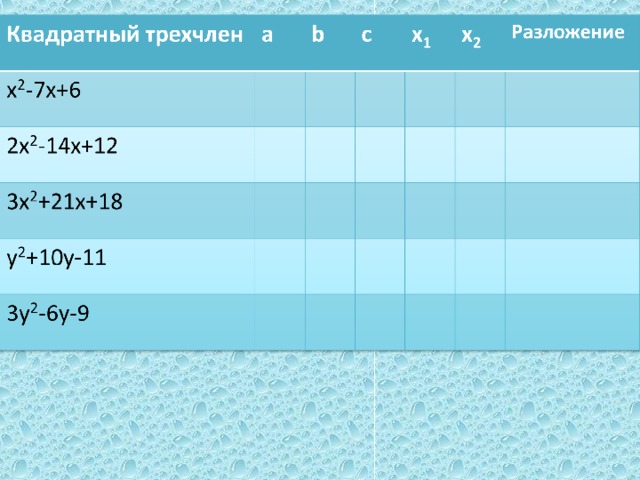
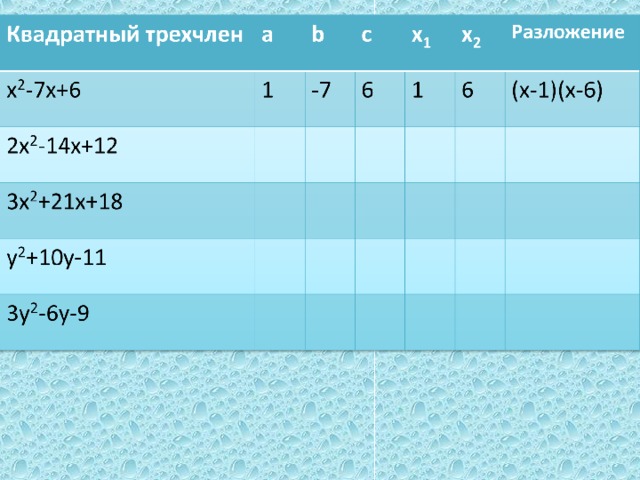
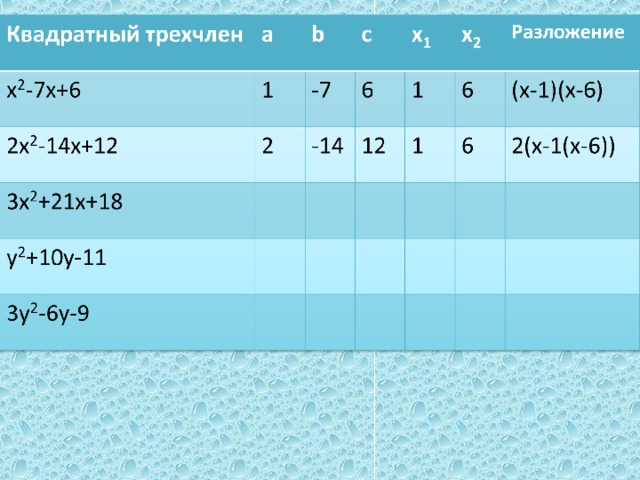
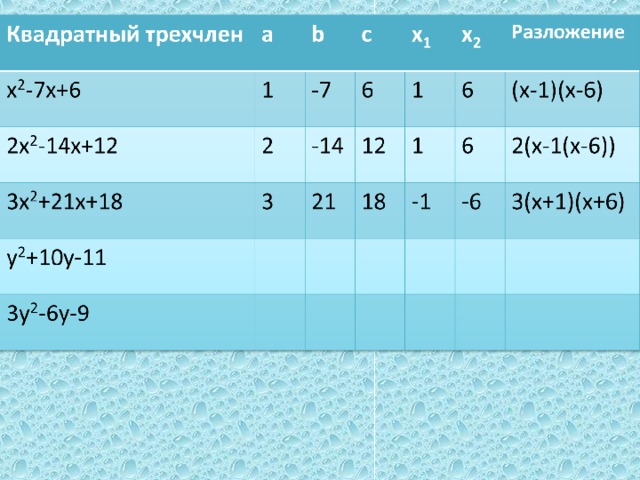
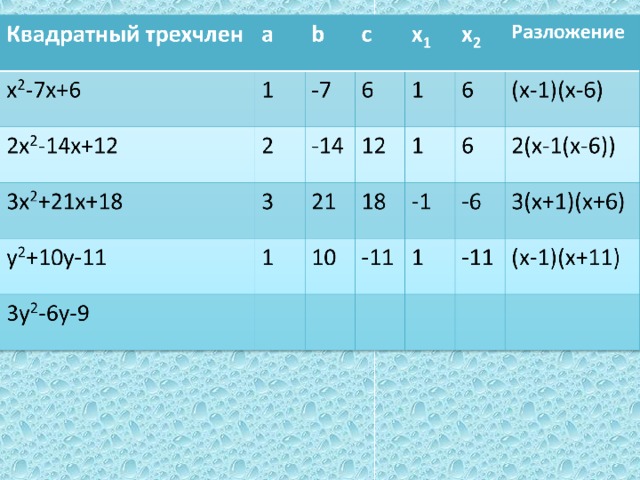
| -Перейдем к решению практических заданий. (на доске уже записан весь перечень номеров). №76(а),г)); №77(а),в)); №78(а). Один из учеников вызывается к доске. -Что требуется сделать в задании? -Что для этого надо знать? -Как найти корни квадратного трехчлена? -или В результате проделанной работы на доске и в тетради должны появится следующие записи: -Хорошо. С первым заданием справились. Следующие решаем по аналогии.
| -разложить квадратный трехчлен на множители. -старший коэффициент и корни -надо решить квадратное уравнение. -или воспользоваться теоремой Виета или ее следствиями. дети записывают № 76 а) 3х2-24х+21, а=3. Для того чтобы разложить квадратный трехчлен на множители решим квадратное уравнение: 3х2-24х+21=0; х2-8х+7=0; Так как а+b+c=0, то х1=1,х2=7. По теореме о разложении квадратного трехчлена на множители, получим: 3х2-24х+21=3х-1)(х-7). г) х2-12х+20, а=1. Для того чтобы разложить квадратный трехчлен на множители решим квадратное уравнение: х2-12х+20=0; D=144-4*20=64; D0 →2 корня х1= По теореме о разложении квадратного трехчлена на множители, получим: х2-12х+20=(х-2)(х-10). № 77 а) 2х2-2х+ Для того чтобы разложить квадратный трехчлен на множители решим квадратное уравнение: 2х2-2х+ D=4-4=0; D=0 →1 корня х1,2= По теореме о разложении квадратного трехчлена на множители, получим: 2х2-2х+ в) 16х2+24х+9=0; (4х)2+2*4*3х+32=0; (4х+3)2=0 Значит, 16х2+24х+9=(4х+3)2
| |
| Проверочный самоконтроль | ||
| На экране появляются следующие задания (слайд № 8) Выберите верное разложение 1 вариант 2х2-12х+16= 1. (x-2)(x-4) 2. 2(x-6)(x+3) 3. 2(x-4)(x-2) 4. 2(x-2)(x-6)
2 вариант 3х2-24х+45= 1. 24(x-2)(x-5) 2. 3(x-6)(x+3) 3. (x-3)(x-5) 4. 3(x-3)(x-5) - Хорошо, сейчас каждый из вас попробовал решить самостоятельно задание. Большинство из вас справились. Молодцы. | Дети самостоятельно решают на мессах. Когда все решат, учитель просит поднять карточки с номером ответа. | |
| Подведение итогов урока | ||
| Итак, подведем итоги урока: -Что нового вы узнали на сегодняшнем уроке? Как именно?
-Что надо сделать чтобы разложить квадратный трехчлен на множители?
-Мы реализовали наши цели. | -что квадратный трехчлен можно раскладывать намного проще, нежели мы это делали раньше. -с использованием теоремы о разложении квадратного трехчлена на множители. -надо найти его корни, определить старший коэффициент и подставить в формулу.
-Да
| |
| Постановка домашнего задания | ||
| Домашнее задание состоит и 2-х частей: Базовая часть: п.6 (прочитать, разобрать примеры, выучить формулировку теоремы) № 76 (б,в), № 77(б,г) Часть по выбору: -Средний уровень: №79(б). -Повышенный уровень: № 81(а), разобраться с доказательством теоремы. Подготовить план доказательства. |
| |
| Рефлексия | ||
| Возьмите пожалуйста небольшой листочек бумаги, подпишите свою фамилию, нарисуйте пожалуйста числовой луч , отметьте точки от 0 до 10. На этом луче расположите 3 точки: З(знание темы), Н(настроение в конце урока), Д(внутренне состояние души) соответствующим образом. Спасибо за внимание. |
| |

 Получите свидетельство
Получите свидетельство Вход
Вход



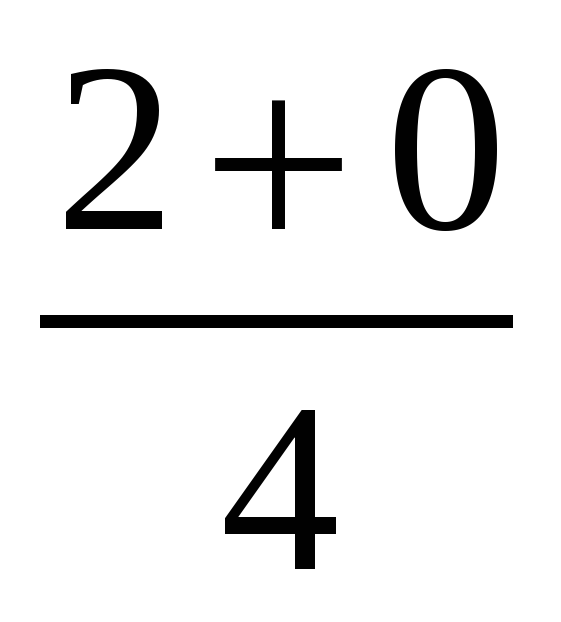 =
=


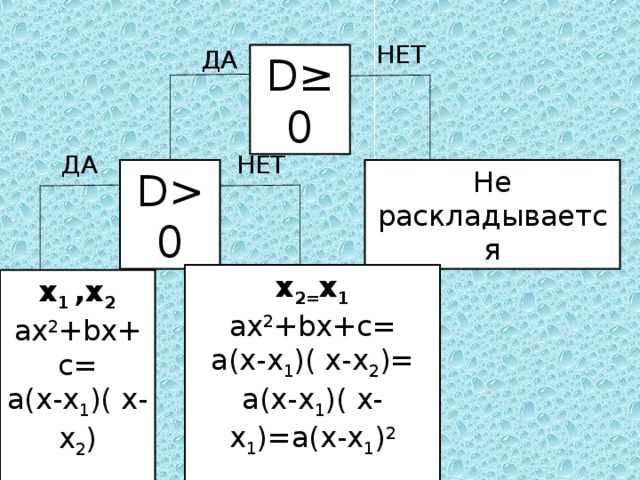 0 x 2 = x 1 ax 2 +bx+c= a(x-x 1 )( x-x 2 ) = a(x-x 1 )( x-x 1 ) = a(x-x 1 ) 2 x 1 ,x 2 ax 2 +bx+c= a(x-x 1 )( x-x 2 )" width="640"
0 x 2 = x 1 ax 2 +bx+c= a(x-x 1 )( x-x 2 ) = a(x-x 1 )( x-x 1 ) = a(x-x 1 ) 2 x 1 ,x 2 ax 2 +bx+c= a(x-x 1 )( x-x 2 )" width="640"
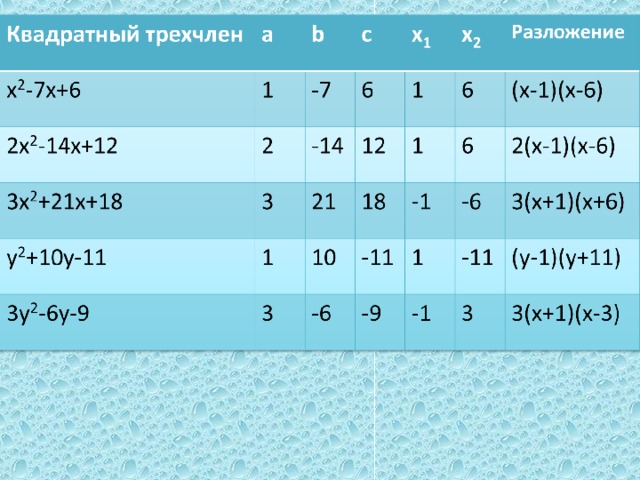









 Разложение квадратного трехчлена на множители (384.05 KB)
Разложение квадратного трехчлена на множители (384.05 KB)
 0
0 520
520 9
9 Нравится
0
Нравится
0


