I .Пояснительная записка.
Рабочая программа учебного курса по алгебре для 7 класса составлена в соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования, Концепцией духовно-нравственного развития учащихся, примерной программы общеобразовательных учреждений по алгебре 7–9 классы, к учебному комплексу для 7-9 классов автора Мордкович (Программы. Математика. 5-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М. Мнемозина, 2012. – 64 с.)
Программа по алгебре составлена на основе Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном стандарте основного общего образования с учётом преемственности программ для начального образования по математике.
В ней также учитываются доминирующие идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование гражданской идентичности, коммуникативных качеств личности и способствуют формированию ключевой компетенции – умения учиться.
Курс алгебры 7 класса является базовым для математического образования и развития школьников. Алгебраические знания и умения необходимы для изучения геометрии, алгебры и математического анализа в 10-11 классах, а также смежных дисциплин.
Практическая значимость школьного курса алгебры 7 класса состоит в том, что предметом её изучения являются количественные отношения и процессы реального мира, описанные математическими моделями. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Одной из основных целей изучения алгебры является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения алгебры формируется логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение алгебре даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения. В процессе изучения алгебры школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную письменную и устную речь.
Знакомство с историей развития алгебры как науки формирует у учащихся представление об алгебре как части общечеловеческой культуры. Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируются содержательное раскрытие математических понятий, толкование сущности математических методов, и области их применения, демонстрация возможности применения теоретических знаний для решения разнообразных задач прикладного характера, например решение текстовых задач, денежных и процентных расчетов, умение пользоваться количественной информацией, представленной в различных формах, умение читать графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определённого типа.
II. Общая характеристика учебного предмета «Алгебра»
Алгебра как содержательный компонент математического образования в основной школе нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
III. Описание места учебного предмета «Алгебра»
в учебном плане
В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Алгебра» изучается с 7-го по 11-й класс. Согласно федеральному базисному учебному плану, на изучение алгебры в 7-м классе отводится не менее 170 часов, из расчета 5 часов в неделю, из школьного компонента выделен 1 час в неделю. Таким образом, учебный план МБОУ «СОШ №3» содержит в 7-ом классе 6 часов в неделю или 204 часа в год. Дополнительные часы используются для расширения и углубления знаний и умений по отдельным темам всех разделов курса, для решения заданий повышенного уровня математической подготовки учащихся, для освоения более продвинутого математического аппарата, математических способностей. Данная рабочая программа позволяет осуществлять дифференцированный подход к организации образовательного процесса на уроках алгебры в 7 классе.
IV. Личностные, метапредметные и предметные
результаты освоения содержания курса алгебры 7 класса
Изучение алгебры по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
Личностные результаты:
1) воспитание российской гражданской идентичности; патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
2) ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
3) осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интнресов, а так же на освове формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
4) умение контролировать процесс и результат учебной и математической деятельности;
5) критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
1) умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
2) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действия в рамках предложенных условий и требований, корретировать свои действия в соответствии изменяющейся ситуацей;
3) Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
4) умение устанавливать причинно- следственные связи, строить логические рассуждения, умозаключения ( индуктивное, дедуктивное, по аналогии) и делать выводы;
5) развитие компетентности в области использования информационно-коммуникационных технологий;
6) первоначальные представления о идеях и методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
7) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
8) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение у условиях неполной или избыточной, точной или вероятностной информации;
9) Умение понимать и использовать математические средства наглядности ( графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
10) умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
11) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
1) осознание значения математики в повседневной жизни человека;
2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации
3) развитие умение работать с учебным математическим текстом ( анализировать извлекать необходимую информацию), точно и грамотно излагать свои мысли с применением математической терминологии и символики, проводить классификацию, логические обоснования;
4) владение базовым понятийным аппаратом по основным разделам содержания;
5) систематические знания о функциях и их свойствах;
6) практически значимые математические умения и навыки, их применение к решению математических и нематематических задач, предполагающее умения:
выполнять вычисления с действительными числами;
решать линейные уравнения с одной переменной и системы линейных уравнений с двумя переменными;
решать текстовые задачи с помощью уравнений и систем уравнений;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
выполнять тождественные преобразования алгебраических выражений;.
исследовать линейные функции и строить их графики.
V. Примерные нормы оценки знаний, умений и навыков
обучающихся.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя
Ответ оценивается отметкой «4»,если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
Общая классификация ошибок.
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков
VI. Содержание учебного материала курса алгебры
7 класса.
1. Математический язык. Математическая модель. 17 часов
Числовые и алгебраические выражения. Первые представления о математическом языке и о математической модели. Линейные уравнения как математические модели реальных ситуаций.
2. Линейная функция. 14 часов
Координатная прямая, виды промежутков на ней. Координатная плоскость. Линейное уравнение с двумя переменными и его график. Отыскание наибольших и наименьших значений линейной функции на заданном промежутке. Прямая пропорциональность и её график. Взаимное расположение графиков линейных функций. Возрастание и убывание линейной функции.
3. Степень с натуральным показателем и её свойства. 8 часов
Определение степени с натуральным показателем, таблицы основных степеней. Степень с нулевым показателем.
4. Одночлены. Арифметические операции над одночленами. 11 часов
Понятие одночлена, его стандартный вид. Сложение и вычитание одночленов, умножение одночленов, возведение одночлена в натуральную степень. Деление одночлена на одночлен.
5. Многочлены. Арифметические операции над многочленами. 20 часов
Понятие многочлена, его стандартный вид. Сложение и вычитание многочленов. Умножение многочлена на одночлен, умножение многочлена на многочлен. Формулы сокращённого умножения. Деление многочлена на одночлен.
6. Разложение многочленов на множители. 24 часа
Понятие о разложении многочлена на множители. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращённого умножения. Комбинирование различных приёмов. Понятие тождества и тождественного преобразования алгебраического выражения. Первые представления об алгебраических дробях: сокращение алгебраических дробей.
7. Системы двух линейных уравнений с двумя переменными. 17 часов
Основные понятия, связанные с системами двух линейных уравнений с двумя переменными. Графическое решение систем. Метод подстановки, метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).
8. Функция y = x2. 12 часов
Функция y = x2, её свойства и график. Отыскание наибольших и наименьших значений функции на заданных промежутках. Графическое решение уравнений. Функции заданные разными формулами на различных промежутках («кусочные» функции). Понятие о непрерывных и разрывных функциях. Разъяснение смысла записи y = f(x). Функциональная символика.
9. Повторение 12 часов
VII. Описание учебно-методического и материально-технического обеспечения образовательного процесса
по предмету «Алгебра»
Учебно-методическое обеспечение
1. Программные документы:
Примерная программа среднего (полного) образования по математике для общеобразовательных школ, гимназий, лицеев. М: «Дрофа», 2013.
2. Учебники и учебно-методическая литература:
А.Г. Мордкович. Алгебра-7. Часть 1: Учебник для общеобразовательных учреждений – М.: Мнемозина, 2013.
А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра-7. Часть 2: Задачник для общеобразовательных учреждений – М.: Мнемозина, 2013.
А.Г. Мордкович. Алгебра, 7-9. Пособие для учителей – М.: Мнемозина, 2013.
Ю.П. Дудницын, Е.Е. Тульчинская. Алгебра-7. Контрольные работы (под ред. А.Г. Мордковича) – М: Мнемозина, 2012.
А.Г. Мордкович, Е.Е. Тульчинская. Алгебра 7-9. Тесты. – М: Мнемозина, 2012.
Л.А. Александрова. Алгебра-7. Самостоятельные работы (под ред. А.Г. Мордковича) – М: Мнемозина, 2012.
3. Материально техническое обеспечение
Раздаточный дидактический материал
Тесты
Тематические таблицы
Компьютер , диапроектор
4. Интернет-ресурсы
www.sch2000.ru
www.ege.moipkro.ru
www.fipi.ru
ege.edu.ru
www.mioo.ru
www.1september.ru
www.math.ru
www.allmath.ru
www.uztest.ru
http://schools.techno.ru/tech/index.html
http://www.catalog.alledu.ru/predmet/math/more2.html
http://shade.lcm.msu.ru:8080/index.jsp
http://wwwexponenta.ru/
http://comp-science.narod.ru/
http://methmath.chat.ru/index.html
http://www.mathnet.spb.ru/
http://vip.km.ru/vschool/demo/education.asp?subj=292
http://som.fio.ru/subject.asp?id=10000191
http:// education.bigli.ru
http://informatika.moipkro.ru/intel/int mat.shtml
http://schools.techno.ru/tech/index.html
http://kvant.mccme.ru/index.html
http://math.ournet.md/indexr.html
http://www.nsu/ru/mmf/tvims/probab.html
http://www.mccme.ru/mmmf-lrctures/books/
VIII. Планируемые результаты изучения алгебры
1. Алгебраические выражения.
Ученик научится:
оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами;
выполнять преобразование выражений, содержащих степени с натуральным показателями;
выполнять тождественные преобразования выражений на основе правил действий над многочленами;
выполнение разложение многочленов на множители.
Ученик получит возможность:
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования для решения различных задач.
2. Уравнения.
Ученик научится:
решать основные виды рациональных уравнений с одной переменной, системы двух линейных уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных раельных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений и решения систем линейных уравнений с двумя переменными;
Ученик получит возможность:
овладеть специальными приёмами решения линейных уравнений и систем линейных уравнений с двумя переменными; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
3.Функции.
Ученик научится:
понимать и использовать функциональные понятия, язык (термины, символические обозначения)
строить графики линейных функций, исследовать линейные функции на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
Ученик получит возможность:
IX. Тематический план . Алгебра. 7 класс.
( 4 часа в неделю, всего 136 часов
| № п/п | Наименование раздела | Формируемые УУД |
| 1 | Математический язык. Математическая модель. | Метапредметные и личностные УУД:
- формирование представлений о целостности и непрерывности курса математики 5 и 6 класса;
- обобщение и систематизация знаний о числовых выражениях, допустимых и недопустимых значениях переменной выражения, математических утверждениях, математическом языке; выполнении действий с применением арифметических законов, действий с десятичными дробями, действий с обыкновенными дробями, совместные действия с обыкновенными и десятичными дробями;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- развитие умения анализировать полученный ответ, предвидеть последствия своих действий, находить ошибки в рассуждениях, приведших к неверному ответу, исправлять и корректировать ход действий, добиваясь верного решения, умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта, умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- формирование коммуникативной компетентности в общении;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры, умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации Основные виды деятельности (предметные УУД):
- находить значения числовых выражений, а также выражений с переменными при указанных значениях переменных;
- сравнивать значения числовых и буквенных выражений; читать и составлять двойные неравенства;
- выполнять простейшие преобразования выражений: приводить подобные слагаемые, раскрывать скобки в сумме или разности выражений;
- решать уравнения вида ax=b при различных значениях а и b, а также несложные уравнения, сводящиеся к ним;
- использовать аппарат уравнений для решения текстовых задач, интерпретировать результат;
- использовать простейшие статистические характеристики (среднее арифметическое, размах, мода, медиана) для анализа ряда данных в несложных ситуациях |
| 2 | Линейная функция. | Метапредметные и личностные УУД:
- обобщение представлений о прямоугольной системе координат, об абсциссе, ординате;
- формирование представлений о числовых промежутках, числовых лучах, функции и ее графике, линейной функции и ее графике;
- формирование умений построения графика линейной функции. Исследования взаимного расположения графиков линейных функций;
- овладение умением применения алгоритма отыскания координат точки, заданной в прямоугольной системе координат, алгоритма построения точки в прямоугольной системе координат, алгоритма построения графика линейного уравнения ах+bу+с=0;
- овладение навыками решения линейного уравнения с двумя переменными ах+bу+с=0 графическим способом;
- овладение навыком работать с графиками реальных линейных процессов. Знакомство с применением графической информации при изучении предметов школьного цикла, в реальной жизни;
- овладение умением анализировать график реального процесса, извлекать с его помощью требуемую информацию, умением аргументированно излагать и иллюстрировать полученную информацию;
- осознание связи изучаемых понятий с изученным в геометрии, опора на знания, полученные при изучении геометрии, в частности при выработке рационального алгоритма построения линейной функции табличным способом, аргументированное обоснование достаточности двух точек для построения, при обсуждении возможного взаимного расположения графиков;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- развитие умения анализировать полученный ответ, предвидеть последствия своих действий, находить ошибки в рассуждениях, приведших к неверному ответу, исправлять и корректировать ход действий, добиваясь верного решения, умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта, умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- сформированность коммуникативной компетентности в общении;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры, умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
Основные виды деятельности (предметные УУД):
- вычислять значения функции, заданной формулой, составлять таблицы значений функции;
- по графику функции находить значение функции по известному значению аргумента и решать обратную задачу;
- строить графики прямой пропорциональности и линейной функции, описывать свойства этих функций;
- понимать, как влияет знак коэффициента k на расположение в координатной плоскости графика функции у=kх, где 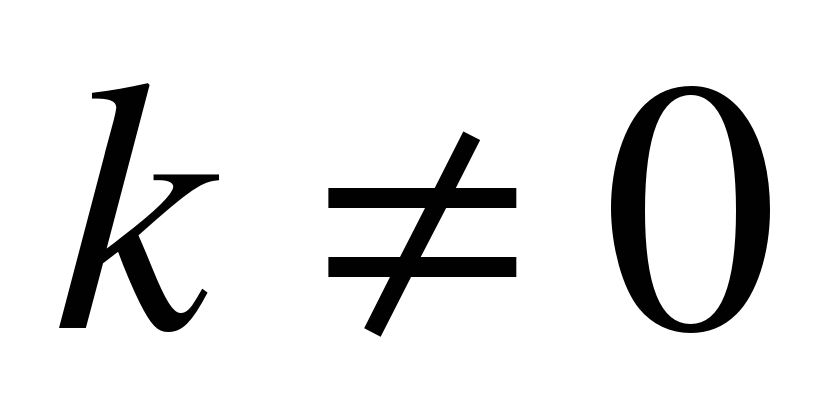 , как зависит от значений k и b взаимное расположение графиков двух функций вида у=kх+b; , как зависит от значений k и b взаимное расположение графиков двух функций вида у=kх+b;
- интерпретировать графики реальных зависимостей, описываемых формулами вида у=kх, где 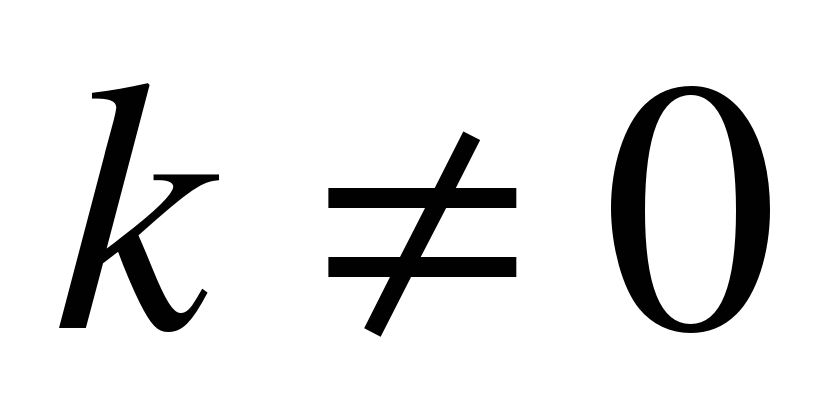 и у=kх+b и у=kх+b |
| 3 | Степень с натуральным показателем и ее свойства | Метапредметные и личностные УУД:
- свободное владение терминологией, владение базовым понятийным аппаратом;
- обобщение знаний, полученных на предыдущих этапах обучения;
- формирование представлений о степени с натуральным показателем, о степени с нулевым показателем, о параболе, о кубической параболе, квадратичной функции и ее графике, о функции у=х3 и ее графике;
- формирование умений составления таблиц основных степеней и ее применение при решении заданий, строить графики функций y=x2 и у=х3 , определять участки возрастания и убывания функции;
- овладение умением применения свойств степени с натуральным показателем при решении задач, выполнять действие умножения и деления степеней с одинаковыми показателями, описывать свойства функции по ее графику, читать графики функции;
- овладение навыками решения уравнений, содержащих степень с натуральным показателем, строить график кусочно-заданной функции, применяя алгоритм графического решения уравнения;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- развитие умения анализировать полученный ответ, предвидеть последствия своих действий, находить ошибки в рассуждениях, приведших к неверному ответу, исправлять и корректировать ход действий, добиваясь верного решения, умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта, умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- сформированность коммуникативной компетентности в общении;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры, умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
Основные виды деятельности (предметные УУД):
- вычислять значения выражений вида 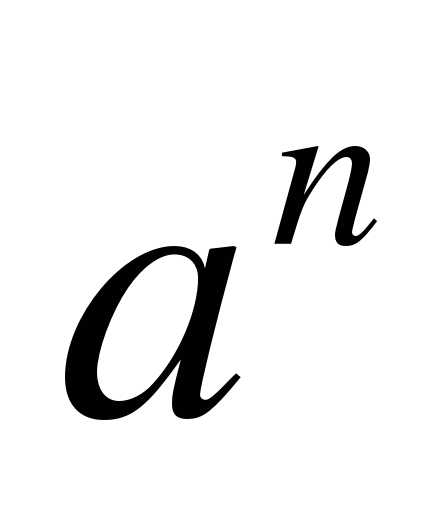 , где а - произвольное число, n - натуральное число, устно и письменно, а также с помощью калькулятора; , где а - произвольное число, n - натуральное число, устно и письменно, а также с помощью калькулятора;
- формулировать, записывать в символической форме и обосновывать свойства степени с натуральным показателем;
- применять свойства степени для преобразования выражений
- выполнять умножение одночленов и возведение одночленов в степень;
- строить графики функций y=x2 и y=x3;
- решать графически уравнения х2=kх+b, х3=kх+Ь, где k и b - некоторые числа |
| 4 | Одночлены и многочлены, действия над ними. | Метапредметные и личностные УУД
- формирование представлений о многочлене, о приведении подобных членов многочлена, о стандартном виде многочлена;
- формирование умений представлять многочлен в стандартном виде, выполнять арифметические действия над многочленами;
- овладение умением складывать, вычитать, умножать и делить многочлены;
- овладение навыками приведения подобных членов многочлена, решения уравнений, предполагающих приведение многочленов к стандартному виду;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- сформированность коммуникативной компетентности в общении;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры, умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
Основные виды деятельности (предметные УУД):
- записывать многочлен в стандартном виде, определять степень многочлена;
- выполнять сложение и вычитание многочленов, умножение одночлена на многочлен и многочлена на многочлен;
- выполнять разложение многочленов на множители, используя вынесение множителя за скобки и способ группировки;
- применять действия с многочленами при решении разнообразных задач, в частности при решении текстовых задач с помощью уравнений
|
| 5 | Разложение многочленов на множители. | Метапредметные и личностные УУД:
- свободное владение терминологией, владение базовым понятийным аппаратом;
- формирование представлений о разложении многочлена на множители с использованием формул сокращенного умножения;
- овладение умением преобразования выражений с использованием формул сокращенного умножения, выделения полного квадрата;
- овладение навыками решения уравнений, выделения полного квадрата, решения уравнений с применением формул сокращенного умножения
- формирование вариативности мышления, умения обосновывать выбор или невозможность решения требуемым способом в конкретной ситуации;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- развитие умения анализировать полученный ответ, предвидеть последствия своих действий, находить ошибки в рассуждениях, приведших к неверному ответу, исправлять и корректировать ход действий, добиваясь верного решения, умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта, умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- сформированность коммуникативной компетентности в общении;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры, умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; слушать партнера; формулировать, аргументировать и отстаивать свое мнение;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
Основные виды деятельности (предметные УУД):
- доказывать справедливость формул сокращенного умножения, применять их в преобразованиях целых выражений в многочлены, а также для разложения многочленов на множители;
- использовать различные преобразования целых выражений при решении уравнений, доказательстве тождеств, в задачах на делимость, в вычислении значений некоторых выражений с помощью калькулятора |
| 6 | Системы линейных уравнений | Метапредметные и личностные УУД:
- владение базовым понятийным аппаратом;
- формирование представлений о системе двух линейных уравнений с двумя переменными, о несовместимости системы, о неопределенной системе уравнений;
- овладение умением решения систем линейных уравнений графическим методом, методом подстановки и методом алгебраического сложения;
- овладение навыками составления математической модели реальных ситуаций в виде системы двух линейных уравнений с двумя переменными;
- овладение навыками решения задач, составляя математическую модель реальной ситуации;
- развитие логического, математического мышления и интуиции, творческих способностей в области математики, способности обучающихся к саморазвитию и самообразованию;
- практическое применение полученных знаний, представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации, первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
- развитие умения анализировать полученный ответ, предвидеть последствия своих действий, находить ошибки в рассуждениях, приведших к неверному ответу, исправлять и корректировать ход действий, добиваясь верного решения, умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта, умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения, анализ, синтез, обобщение полученных знаний;
- сформированность коммуникативной компетентности в общении;
- формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
- умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
Основные виды деятельности (предметные УУД):
- определять, является ли пара чисел решением данного уравнения с двумя переменными;
- находить путем перебора целые решения линейного уравнения с двумя переменными;
- строить график уравнения ах+by=с, где а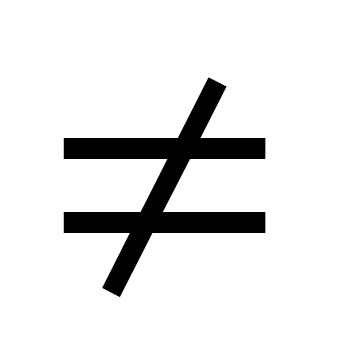 0 или b 0 или b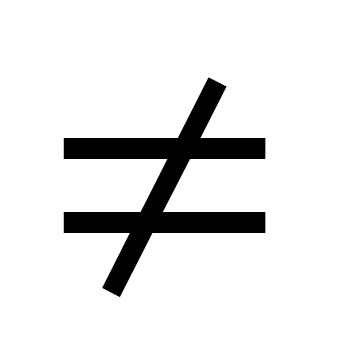 0; 0;
- решать графическим способом системы линейных уравнений с двумя переменными
- применять способ подстановки и способ сложения при решении систем линейных уравнений с двумя переменными
- решать текстовые задачи, используя в качестве алгебраической модели систему уравнений;
- интерпретировать результат, полученный при решении системы |
| 7 | Обобщающее повторение алгебры 7 | Основная задача: выявить пробелы в знаниях каждого учащегося и помочь ему в обнаружении материала, усвоенного им на недостаточном уровне, в коррекции знаний. Формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни Учащимся, усвоившим материал на хорошем уровне помочь выйти за рамки изученного путем решения задач проблемного характера, повышенного уровня, помощи "отстающим" |


 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре для 7 класса (0.17 MB)
Рабочая программа по алгебре для 7 класса (0.17 MB)
 0
0 608
608 42
42 Нравится
0
Нравится
0




