Администрация муниципального образования -
Михайловский муниципальный район Рязанской области
Муниципальное образовательное учреждение
«Михайловская средняя общеобразовательная школа № 2»
муниципального образования – Михайловский муниципальный район Рязанской области
«Рассмотрено» «Согласовано»
на МО учителей физико-математического цикла
Зам. директора по УВР Протокол № 1 от 29 августа 2023 г. ___________ /Ракова О.И./
Руководитель МО__________ /Панова И.А./ от «29» августа 2023 г.
«Утверждаю»
Директор МОУ «Михайловская СОШ № 2»
___________ Савостьянов А.П.
Приказ № 188
от «30» августа 2023 г.
Рабочая программа
учебного предмета
«Математика (алгебра)»
для 8 класса основного общего образования
на 2023-2024 учебный год.
(программа может быть использована для реализации заочной формы обучения
с применением дистанционных образовательных технологий)
Автор-составитель:
учитель математики
Кузнецова Е.В.
2023 – 2024 учебный год
г. Михайлов
I .Пояснительная записка.
- Настоящая программа по алгебре для основной общеобразовательной школы в 8 классе составлена на основе федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерных программ по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263), примерной программы общеобразовательных учреждений по алгебре 7–9 классы, к учебному комплексу для 7-9 классов (авторы А. Г. Мерзляк, В. Б. Полонский, М. С. Якир– М: Вентана – Граф, 2013 – с. 192)
Программа по алгебре составлена на основе Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном стандарте основного общего образования с учётом преемственности программ для начального образования по математике.
В ней также учитываются доминирующие идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование гражданской идентичности, коммуникативных качеств личности и способствуют формированию ключевой компетенции – умения учиться.
Курс алгебры класса является базовым для математического образования и развития школьников. Алгебраические знания и умения необходимы для изучения геометрии, алгебры и математического анализа в 10-11 классах, а также смежных дисциплин.
Практическая значимость школьного курса алгебры 8 класса состоит в том, что предметом её изучения являются количественные отношения и процессы реального мира, описанные математическими моделями. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Одной из основных целей изучения алгебры является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения алгебры формируется логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение алгебре даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
В процессе изучения алгебры школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную письменную и устную речь.
Знакомство с историей развития алгебры как науки формирует у учащихся представление об алгебре как части общечеловеческой культуры.
Основные развивающие и воспитательные цели
Развитие:
- ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
- математической речи;
- сенсорной сферы; двигательной моторики;
- внимания; памяти;
- навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов
Воспитание:
· культуры личности, отношения к математике как к части общечеловеческой культуры,
· понимание значимости математики для научно-технического прогресса;
· волевых качеств;
· коммуникабельности;
· ответственности.
«Алгебра»
Алгебра как содержательный компонент математического образования в основной школе нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики; овладение навыками дедуктивных рассуждений. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
III. Описание места учебного предмета «Алгебра» в учебном плане
В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Алгебра» изучается с 7-го по 11-й класс. Согласно федеральному базисному учебному плану, на изучение алгебры в 8-м классе отводится не менее 108 часов, из расчета 3 часа в неделю, из школьного компонента выделен 1 час в неделю. Таким образом, учебный план МОУ Михайловская «СОШ №2» содержит в 8-ом классе 4 часа в неделю или 140 часов в год.
IV. Личностные, метапредметные
и предметные результаты
освоения содержания курса алгебра 8 класса.
Изучение алгебры по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
Личностные результаты:
1) воспитание российской гражданской идентичности; патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
2) ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
3) осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интнресов, а так же на освове формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;
4) умение контролировать процесс и результат учебной и математической деятельности;
5) критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
1) умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познавательной деятельности;
2) умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действия в рамках предложенных условий и требований, корректировать свои действия в соответствии изменяющейся ситуацией;
3) Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
4) умение устанавливать причинно- следственные связи, строить логические рассуждения, умозаключения ( индуктивное, дедуктивное, по аналогии) и делать выводы;
5) развитие компетентности в области использования информационно-коммуникационных технологий;
6) первоначальные представления о идеях и методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
7) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
8) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
9) Умение понимать и использовать математические средства наглядности ( графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
10) умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
11) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
1) осознание значения математики в повседневной жизни человека;
2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации
3) развитие умение работать с учебным математическим текстом ( анализировать извлекать необходимую информацию), точно и грамотно излагать свои мысли с применением математической терминологии и символики, проводить классификацию, логические обоснования;
4) владение базовым понятийным аппаратом по основным разделам содержания;
5) систематические знания о функциях и их свойствах;
6) практически значимые математические умения и навыки, их применение к решению математических и нематематических задач, предполагающее умения:
выполнять вычисления с действительными числами;
решать текстовые задачи с помощью уравнений и систем уравнений;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
выполнять тождественные преобразования алгебраических выражений;.
исследовать линейные функции и строить их графики.
V. Примерные нормы оценки знаний, умений и навыков обучающихся.
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя
Ответ оценивается отметкой «4»,если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков
VI. Содержание учебного материала курса алгебры
8 класса.
Алгебраические выражения
Рациональные выражения. Целые выражения. Дробные выражения. Рациональная дробь. Основное свойство рациональной дроби. Сложение, вычитание, умножение и деление рациональных дробей. Возведение рациональной дроби в степень. Тождественные преобразования рациональных выражений. Степень с целым показателем и её свойства. Квадратные корни. Арифметический квадратный корень и его свойства. Тождественные преобразования выражений, содержащих квадратные корни.
Уравнения
Квадратное уравнение. Формула корней квадратного уравнения. Теорема Виета. Рациональные уравнения. Решение рациональных уравнений, сводящихся к линейным или к квадратным уравнениям. Решение текстовых задач с помощью рациональных уравнений..
Числовые множества
Множество и его элементы. Способы задания множеств. Равные множества. Пустое множество. Подмножество. Операции над множествами. Иллюстрация соотношений между множествами с помощью диаграмм Эйлера. Множества натуральных, целых, рациональных чисел. Рациональное число как дробь вида m/n,
где m € Z, п € N, и как бесконечная периодическая десятичная дробь. Представление об иррациональном числе. Множество действительных чисел. Представление действительного числа в виде бесконечной непериодической десятичной дроби. Сравнение действительных чисел. Связь между множествами N, Z, Q, R.
Функции
Числовые функции Функциональные зависимости между величинами. Понятие функции. Функция как математическая модель реального процесса. Область определения и область значения функции. Способы задания функции. График функции. Построение графиков функций с помощью преобразований фигур. Нули функции. Промежутки знакопостоянства функции. Промежутки возрастания и убывания функции. Обратная пропорциональность, квадратичная функция, функция у =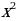 , её свойства и графики.
, её свойства и графики.
Алгебра в историческом развитии
Зарождение алгебры, книга о восстановлении и противопоставлении Мухаммеда аль- Хорезми. История формирования математического языка. Как зародилась идея координат. Открытие иррациональности. Из истории возникновения формул для решения уравнений 3-й и 4-й степеней. История развития понятия функции..
VII. Описание учебно-методического и материально-технического обеспечения
образовательного процесса по предмету «Алгебра»
Учебно-методическое обеспечение
1. Программные документы:
Примерная программа среднего (полного) образования по математике для общеобразовательных школ, гимназий, лицеев. М: «Дрофа», 2008.
2. Учебники и учебно-методическая литература:
Программа по курсам математики (5-6 классы), алгебры (7-9 классы) и геометрии (7-9 классы) созданная на основе единой концепции преподавания математики в средней школе, разработанной. А. Г. Мерзляком, В.Б. Полонским, М.С. Якиром- авторами учебников Алгебра-7, Геометрия-7, включённых в систему « Алгоритм успеха»
А. Г. Мерзляк, В.Б. Полонский, М.С. Якир Алгебра-8
А. Г. Мерзляк, В.Б. Полонский, М.С. Якир Алгебра 8. Дидактический материал.
3. Материально техническое обеспечение
Раздаточный дидактический материал
Тесты
Тематические таблицы
Компьютер
VIII. Планируемые результаты изучения алгебры
в 8 классе
Алгебраические выражения
Ученик научится: оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами; оперировать понятием квадратного корня, применять его в вычислениях; выполнять преобразование выражений, содержащих степени с целыми показателями и квадратные корни; выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями; выполнять разложение многочленов на множители.
Ученик получит возможность: выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов; применять тождественные преобразования для решения задач из различных разделов курса.
Уравнения
Ученик научится: решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными; понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом; применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Ученик получит возможность: овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики; применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
В повседневной жизни и при изучении других предметов:
составлять и решать квадратные уравнения, уравнения, к ним сводящиеся, при решении задач других учебных предметов;
выполнять оценку правдоподобия результатов, получаемых при решении квадратных уравнений при решении задач других учебных предметов;
выбирать соответствующие уравнения, для составления математической модели заданной реальной ситуации или прикладной задачи;
уметь интерпретировать полученный при решении уравнения результат в контексте заданной реальной ситуации или прикладной задачи
Числовые множества
Ученик научится: понимать терминологию и символику, связанные с понятием множества, выполнять операции над множествами; использовать начальные представления о множестве действительных чисел.
Ученик получит возможность: развивать представление о множествах; развивать представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике; развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
В повседневной жизни и при изучении других предметов:
использовать графическое представление множеств для описания реальных процессов и явлений, при решении задач других учебных предметов
оценивать результаты вычислений при решении практических задач;
выполнять сравнение чисел в реальных ситуациях;
составлять числовые выражения при решении практических задач и задач из других учебных предметов
Функции
Ученик научится: понимать и использовать функциональные понятия, язык (термины, символические обозначения); строить графики элементарных функций, исследовать свойства числовых функций на основе изучения поведения их графиков; понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
Ученик получит возможность: проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.); использовать функциональные представления и свойства функций решения математических задач из различных разделов курса.
В повседневной жизни и при изучении других предметов:
использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.);
использовать свойства линейной функции и ее график при решении задач из других учебных предметов
Формы организации учебного процесса:
Технологии: дифференцированное обучение, обучение с применением опорных схем, ИКТ.
Формы проведения занятий: лекции, комбинированные уроки, практикумы, повторительно-обобщающие уроки.
Обучение несет деятельностный характер, акцент делается на обучение через практику, продуктивную работу учащихся в малых группах, использование межпредметных связей, развитие самостоятельности учащихся и личной ответственности за принятие решений. Будут созданы условия для самореализации школьников: участие в соревнованиях, презентациях, семинарах, конкурсах, олимпиадах, что должно способствовать активизации их самостоятельной деятельности, развитию креативности и формированию функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах.
Разноуровневое обучение позволит каждому ученику приобрести предметную компетентность, достичь соответствующего уровня планируемых результатов, развить коммуникативные способности, овладеть навыками коллективной деятельности, научиться работать самостоятельно с учебным материалом.
Формы и методы контроля ЗУН: самостоятельные работы, тесты, контрольные работы
IX. Тематический план .
| № п/п | Наименование раздела | Кол-во часов | Формируемые УУД |
|
1
|
Повторение
Рациональные выражения |
7
55
|
Личностные : Формировать интерес к изучению темы и желание применять полученные знания на практике; ответственное отношение к обучению, умение представлять результат своей деятельности, умение соотносить полученный результат с поставленной целью, умение контролировать процесс учебной и математической деятельности, способность осознанного выбора построения дальнейшей индивидуальной траектории, умение формулировать собственное мнение, планировать свои действия в соответствии с учебным заданием, развивать навыки самостоятельной работы, готовность к самообразованию и решению творческих задач, , развивать готовность к самообразованию и решению творческих задач, развивать навыки самостоятельной работы, анализа своей работы, формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные: Формировать умение корректировать свои действия в соответствии с изменяющейся ситуацией, использовать приобретённые знания в практической деятельности, использовать причинно-следственные связи, строить логические рассуждения, умозаключение (индуктивное. дедуктивное и по аналогии) и делать выводы, определять понятия, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, соотносить свои действия с планируемым результатом, развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве ;контролировать действия партнера; поддерживать инициативное сотрудничество в поиске и сборе информации; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы; |
| 2 | Квадратные корни. Действительные числа. | 30 | Личностные : Формировать интерес к изучению темы и желание применять полученные знания на практике; ответственное отношение к обучению, умение представлять результат своей деятельности, умение соотносить полученный результат с поставленной целью, , умение формулировать собственное мнение, планировать свои действия в соответствии с учебным заданием, формировать ответственное отношение к обучению, готовность к саморазвитию и сомообразованию на основе мотивации к обучению и познанию, независимость суждений развивать навыки самостоятельной работы, , формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики. Метапредметные: Формировать умение понимать и использовать математические средства наглядности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией, умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни, использовать приобретённые знания в практической деятельности, использовать причинно-следственные связи, строить логические рассуждения, умозаключение (индуктивное. дедуктивное и по аналогии) и делать выводы, определять понятия и делать выводы , формировать умение самостоятельно определять цели своего обучения, корректировать свои действия в соответствии с изменяющейся ситуацией, осуществлять контроль своей деятельности в процессе достижения результата, умение устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации , соотносить свои действия с планируемым результатом, формировать представление об идеях и методах математики как об универсальном языке науки и техники. учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве ;контролировать действия партнера; поддерживать инициативное сотрудничество в поиске и сборе информации; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы; |
| 3 | Квадратные уравнения | 36 | Личностные : Формировать интерес к изучению темы и желание применять полученные знания на практике; планировать свои действия в соответствии с учебным заданием, ответственное отношение к обучению, умение представлять результат своей деятельности, умение контролировать процесс учебной и математической деятельности, способность осознанного выбора построения дальнейшей индивидуальной траектории, умение формулировать собственное мнение, формировать ответственное отношение к обучению, готовность к саморазвитию и самообразованию и решению творческих задач, развивать навыки самостоятельной работы, анализа своей работы. Метапредметные: Формировать умение понимать и использовать математические средства наглядности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией, умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни, использовать приобретённые знания в практической деятельности, использовать причинно-следственные связи, строить логические рассуждения, умозаключение (индуктивное. дедуктивное и по аналогии) и делать выводы, определять понятия и делать выводы , формировать умение самостоятельно определять цели своего обучения, корректировать свои действия в соответствии с изменяющейся ситуацией, осуществлять контроль своей деятельности в процессе достижения результата, умение устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации , соотносить свои действия с планируемым результатом, формировать представление об идеях и методах математики как об универсальном языке науки и техники. учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве ;контролировать действия партнера; поддерживать инициативное сотрудничество в поиске и сборе информации; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы; |
| 4 | Повторение и систематизация учебного материала | 8 | Личностные : владеть общим приемом решения задач; осуществлять сравнение и классификацию по заданным критериям; ориентироваться на разнообразие способов решения задач; выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; произвольно и осознанно владеть общим приемом решения задач. различать способ и результат действия; вносить необходимые дополнения и коррективы в план и способ действия в случае расхождения эталона, реального действия и его результата; учитывать правило в планировании и контроле способа решения; вносить коррективы и дополнения в составленные планы; осознавать самого себя как движущую силу своего научения, формировать способность к преодолению препятствий и самокоррекции, уметь выполнять работу над ошибками; определять новый уровень отношения к самому себе как субъекту деятельности. Метапредметные: договариваться и приходить к общему решению в совместной работе; аргументировать свою точку зрения, спорить и отстаивать свою позицию; развивать умения итегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми, учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; ясно, логично и точно излагать ответы на поставленные вопросы; критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения и корректировать его, организовывать и планировать учебное сотрудничество с учителем и сверстниками |
| № п/п | Содержание учебного материала | Кол-во часов | Характеристика основных видов деятельности учеников (на уровне учебных действий) | Дата проведения | Домашнее задание |
| Повторение за курс алгебры 7 класса – 7 часов | |||||
| 1 – 2 | Целые выражения | 2 | Формулировать определения, свойства, правила. Вычислять значение выражений с переменными. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночлена в степень. Преобразовывать произведение одночлена и многочлена; суммы, разности и произведения двух многочленов в многочлен. Выполнять разложение многочлена на множители. | 2.09.
| п. 1 – 8 (с. 219 – 222), вариант 2 контрольных работ № 2 – 3 (задания 1 – 4), дидактические материалы по алгебре 7 класс, с. 105 – 107). |
| 3.09. | п. 9 – 13 (с. 223 – 224), вариант 2 контрольных работ № 4 – 5 (задания 1 – 4), дидактические материалы по алгебре 7 класс, с. 107 – 108). | ||||
| 3 | Линейное уравнение с одной переменной. | 1 | Формулировать определение. Решать линейное уравнение. Интерпретировать уравнение как математическую модель реальной ситуации. Решать текстовые задачи с помощью уравнения. | 4.09. | п.14 – 16 (с. 224 – 225), вариант 2 контрольной работы № 1, дидактические материалы по алгебре 7 класс, с. 105). |
| 4 | Координатная плоскость. Функции.
| 1 | Описывать понятия. Вычислять значение функции по заданному значению аргумента. Строить график функции, заданной таблично. По графику функции, являющейся моделью реального процесса, определять характеристики этого процесса. Строить график линейной функции и прямой пропорциональности. Описывать свойства этой функции. | 7.09. | п. 28 (231 – 232), вариант 2 контрольной работы № 6, дидактические материалы по алгебре 7 класс, с. 108). |
| 5 | Системы линейных уравнений с двумя переменными. | 1 | Формулировать определения, свойства. Строить график линейного уравнения с двумя переменными. Решать системы двух линейных уравнений с двумя переиенными. Решать текстовые задачи. | 8.09. | п. 21 – 26 (с.227 – 230), вариант 2 контрольной работы № 7, дидактические материалы по алгебре 7 класс, с.109). |
| 6 | Модуль числа | 1 | Формулировать определение, свойства. Решать уравнения, содержащие модуль. | 9.09. | п. 27 (с. 230), № 17 (вариант 3, дидактические материалы по алгебре 7 класс, с. 69). |
| 7 | Административная контрольная работа. | 1 |
| 10.09. |
|
| Глава 1. Рациональные выражения – 55 часов | |||||
| 8 – 10 | Рациональные дроби. | 3 | Распознавать целые рациональные выражения, дробные рациональные выражения, приводить примеры таких выражений.
Формулировать:
определения: рационального выражения, допустимых значений переменной, тождественно равных выражений, тождества, равносильных уравнений, рационального уравнения, степени с нулевым показателем, степени с целым отрицательным показателем, стандартного вида числа, обратной пропорциональности;
свойства: основное свойство рациональной дроби, свойства степени с целым показателем, уравнений, функции у = k/x;
правила: сложения, вычитания, умножения, деления дробей, возведения дроби в степень; условие равенства дроби нулю.
Доказывать свойства степени с целым показателем.
Описывать графический метод решения уравнений с одной переменной.
Применять основное свойство рациональной дроби для сокращения и преобразования дробей.
Приводить дроби к новому (общему) знаменателю.
Находить сумму, разность, произведение и частное дробей.
Выполнять тождественные преобразования рациональных выражений.
Решать уравнения с переменной в знаменателе дроби.
Применять свойства степени с целым показателем для преобразования выражений.
Записывать числа в стандартном виде.
Выполнять построение и чтение графика функции у = k/x.
| 14.09. | § 1, вопросы 1 – 6, № 4, 6, 21, 22. |
| 15.09. | § 1, № 8, 10, 12. | ||||
| 16.09. | § 1, № 14, 16. | ||||
| 11 – 14 | Основное свойство рациональной дроби. | 4 | 17.09. | § 2, вопросы 1 – 3, № 28, 31, 35, 63. | |
| 21.09. | § 2, № 38, 41, 43, 45.
| ||||
| 22.09. | § 2, № 47, 49, 51.
| ||||
| 23.09. | § 2, № 53, 56, 59.
| ||||
| 15 – 18 | Сложение и вычитание рациональных дробей с одинаковыми знаменателями.
| 4 | 24.09. | § 3, вопросы 1 – 2, № 69, 71, 73.
| |
| 28.09. | § 3, № 75, 77, 79.
| ||||
| 29.09. | § 3, № 82, 84, 86.
| ||||
| 30.09. | § 3, № 88, 90, 96.
| ||||
| 19 – 25 | Сложение и вычитание рациональных дробей с разными знаменателями. | 7 | 1.10. | § 4, вопросы 1 – 2, № 99, 101, 103. | |
| 5.10. | § 4, № 105, 107, 109 (1, 2)
| ||||
| 6.10. | § 4, № 109 (3, 4), 111, 113 (1 – 3). | ||||
| 7.10. | § 4, № 113 (4 – 6), 116, 118.
| ||||
| 12.10. | § 4, № 120, 123, 125.
| ||||
| 13.10. | § 4, № 127, 129, 131.
| ||||
| 14.10. | § 4, задание № 1 «Проверьте себя» в тестовой форме (с. 33 – 34). | ||||
| 26 | Контрольная работа № 1 по теме «Основное свойство рациональной дроби. Сложение и вычитание рациональных дробей». | 1 | 15.10. | § 1 – 4. | |
| 27 – 31 | Умножение и деление рациональных дробей. Возведение рациональной дроби в степень. | 5 | 19.10. | § 5, вопросы 1 – 2, № 145 (1, 3, 5), 147 (1, 3, 5), 150. | |
| 20.10. | § 5, № 145 (2, 4, 6), 147 (2, 4, 6), 150 (2, 4, 6). | ||||
| 21.10. | § 5, вопрос 3, № 152, 154, 172.
| ||||
| 22.10. | § 5, № 156, 159, 161.
| ||||
| 26.10. | § 5, № 163, 165, 167, 169.
| ||||
| 32 – 40 | Тожественные преобразования рациональных выражений. | 9 | 27.10. | § 6, № 177(1 – 2), 179 (1), 181 (1). | |
| 28.10. | § 6, № 177 (3 – 4), 179 (2), 181 (2). | ||||
| 29.10. | § 6, № 177 (5 – 6), 179 (3), 181 (3). | ||||
| 9.11. | § 6, № 177 (7 – 8), 179 (4), 181 (4). | ||||
| 10.11 | § 6, № 183 (1), 185 (1).
| ||||
| 11.11 | § 6, № 183 (2), 185 (2).
| ||||
| 12.11 | § 6, № 187 (1), 189.
| ||||
| 16.11 | § 6, № 187 (2), 191.
| ||||
| 17.11 | § 6, задание № 2 «Проверьте себя» в тестовой форме (с.49 – 50). | ||||
| 41 | Контрольная работа № 2 по теме «Умножение и деление рациональных дробей. Тождественные преобразования рациональных выражений». | 1 | 18.11 | § 5 – 6. | |
| 42 – 45 | Равносильные уравнения. Рациональные уравнения. | 4 | 19.11 | § 7, вопросы 1 – 5, № 208 (1 – 4), 210. | |
| 23.11 | § 7, № 208 (5 – 9), 213 (1 – 3).
| ||||
| 24.11 | § 7, № 215, 218 (1).
| ||||
| 25.11 | § 7, № 218 (2), 220.
| ||||
| 46 – 50 | Степень с целым отрицательным показателем. | 5 | 26.11 | § 8, вопросы 1 – 4, № 233, 235, 239. | |
| 30.11 | § 8, № 241, 243, 247.
| ||||
| 1.12. | § 8, № 249, 253, 255.
| ||||
| 2.12. | § 8, № 255, 257, 261.
| ||||
| 3.12. | § 8, № 264, 268, 272.
| ||||
| 51 – 56 | Свойства степени с целым показателем. | 6 | 7.12. | § 9, вопрос 1, № 275 (1, 3, 5, 7), 277 (1, 3, 5), 279 (1, 3, 5). | |
| 8.12. | § 9, № 275 (2, 4, 6, 8), 277 (2, 4, 6), 279 (2, 4, 6). | ||||
| 9.12. | § 9, № 281 (1, 3, 5), 283 (1, 3), 285 (1). | ||||
| 10.12. | § 9, № 281 (2, 4, 6), 283 (2, 4), 285 (2, 3). | ||||
| 14.12. | § 9, № 287, 290, 292, 294.
| ||||
| 15.12. | § 9, № 297, 299, 301.
| ||||
| 57 – 60 | Функция у = k/x и ее график. | 4 | 16.12. | § 10, вопрос 1, № 314, 316, 318.
| |
| 17.12. | § 10, вопросы 2 – 7, № 321, 323, 325, 327. | ||||
| 21.12. | § 10, № 329, 332, 334, 336.
| ||||
| 22.12. | § 10, № 338, 341, 343.
| ||||
| 61 | Повторение и систематизация учебного материала по теме «Рациональные уравнения. Степень с целым отрицательным показателем. Функция у = k/x и ее график». | 1 | 23.12. | § 7 – 10, задание № 3 «Проверьте себя» в тестовой форме (с. 85 – 86). | |
| 62 | Контрольная работа № 3 по теме «Рациональные уравнения. Степень с целым отрицательным показателем. Функция у = k/x и ее график». | 1 | 24.12. | § 7 – 10. | |
| Глава 2. Квадратные корни. Действительные числа – 30 часов | |||||
| 63 – 65 | Функция у = х2 и ее график. | 3 | Описывать: понятие множества, элемента множества, способы задания множеств; множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел и связи между этими числовыми множествами; связь между бесконечными десятичными дробями и рациональными, иррациональными числами. Распознавать: рациональные и иррациональные числа. Приводить примеры рациональных чисел и иррациональных чисел. Записывать с помощью формул свойства действий с действительными числами. Формулировать: определения: квадратного корня из числа; арифметического квадратного корня из числа, равных множеств, подмножества, пересечения множеств, объединения множеств; свойства: функции у = х2, арифметического квадратного корня, функции у = Доказывать свойства арифметического квадратного корня. Строить графики функций у = х2 и у = Применять понятияе арифметического квадратного корня для вычисления значений выражений. Упрощать выражения. Решать уравнения. Сравнивать значения выражений. Выполнять преобразование выражений с применением вынесения множителя из-под знака корня, внесения множителя под знак корня. Выполнять освобождение от иррациональности в знаменателе дроби, анализ соотношений между числовыми множествами и их элементами. | 28.12. | § 11, вопросы 1 – 6, № 321, 354, 369. |
| 29.12. | § 11, № 356, 358, 360.
| ||||
| 30.12. | § 11, № 362, 365, 367.
| ||||
| 66 – 69 | Квадратные корни. Арифметический квадратный корень. | 4 |
| § 12, вопросы 1 – 5, № 380, 384, 386. | |
|
| § 12, №388, 390
| ||||
|
| § 12, № 398,404, 406.
| ||||
|
| § 12, № 410, 412, 415.
| ||||
| 70 – 71 | Множество и его элементы. | 2 |
| § 13, вопросы 1 – 7, № 427, 434, 435. | |
|
| § 13, № 430, 432, 436. | ||||
| 72 – 73 | Подмножество. Операции над множествами. | 2 |
| § 14, вопросы 1 – 5, № 441, 444, 462. | |
|
| § 14, № 451, 454, 457, 459.
| ||||
| 74 – 76 | Числовые множества. | 3 |
| § 15, вопросы 1 – 5, № 470, 474.
| |
|
| § 15, № 476, 486.
| ||||
|
| § 15, № 479, 481.
| ||||
| 77 – 81 | Свойства арифметического квадратного корня.
| 5 |
| § 16, вопросы 1 – 5, № 497, 498 (1, 3, 5,7, 9, 11), 501 (1, 3, 5) | |
|
| § 16, № 498 (2, 4, 6, 8, 10, 12), 501 (2, 4, 6), 503 (1, 3). | ||||
|
| § 16, № 503 (2, 4), 507 (1, 3, 5).
| ||||
|
| § 16, № 507 (2, 4, 6), 509, 511.
| ||||
|
| § 16, № 513, 517, 519.
| ||||
| 82 – 87 | Тождественные преобразования выражений, содержащих арифметические квадратные корни. | 6 |
| § 17, № 526, 528, 575.
| |
|
| § 17, № 530, 532, 535, 537.
| ||||
|
| § 17, № 539, 541, 543, 545.
| ||||
|
| § 17, № 547, 549, 551, 554, 556.
| ||||
|
| § 17, № 558, 560, 562, 564.
| ||||
|
| § 17, № 566, 568, 570, 572.
| ||||
| 88 – 90 | Функция у = | 3 |
| § 18, вопросы 1 – 7, № 582, 584, 586, 589. | |
|
| § 18, № 591, 593, 595, 597, 599.
| ||||
|
| § 18, № 602, 606, 609, 613.
| ||||
| 91 | Повторение и систематизация учебного материала по теме «Квадратные корни» | 1 |
| § 11 – 18, задание № 4 «Проверьте себя» в тестовой форме (с. 151 – 152). | |
| 92 | Контрольная работа № 4 по теме «Квадратные корни». | 1 |
| § 11 – 18. | |
| Глава 3. Квадратные уравнения – 36 часов | |||||
| 93 – 96 | Квадратные уравнения. Решение неполных квадратных уравнений. | 4 | Распознавать и приводить примеры квадратных уравнений различных видов (полных, неполных, приведенных), квадратных трехчленов. Описывать в общем виде решение неполных квадратных уравнений. Формулировать: определения: уравнения первой степени, квадратного уравнения; квадратного трехчлена, дискримента квадратного уравнения и квадратного трехчлена, корня квадратного трехчлена; биквадратного уравнения; свойства квадратного трехчлена; теорему Виета и обратную ей теорему. Записывать и доказывать формулу корней квадратного уравнения. Исследовать количество корней квадратного уравнения в зависимости от знака его дискриминанта. Доказывать теоремы: Виета (прямую и обратную), о разложении квадратного трехчлена на множители, о свойстве квадратного трехчлена с отрицательным дискриминантом. Описывать на примерах метод замены переменной для решения уравнений. Находить корни квадратных уравнений различных видов. Применять теорему Виета и обратную ей теорему. Выполнять разложение квадратного трехчлена на множители. Находить корни уравнений, которые сводятся к квадратным. Составлять квадратные уравненияы и уравнения, сводящиеся к квадратным, являющиеся математическими моделями реальных ситуаций. |
| § 19, вопросы 1 – 7, № 618, 622, 625. |
|
| § 19, вопрос 8, № 627, 629, 631.
| ||||
|
| § 19, № 634, 636, 639.
| ||||
|
| § 19, № 641, 646, 648.
| ||||
| 97 – 101 | Формула корней квадратного уравнения. | 5 |
| § 20, вопросы 1 – 4, № 658, 660, 662. | |
|
| § 20, № 664, 671, 673, 685.
| ||||
|
| § 20, № 667, 669, 675.
| ||||
|
| § 20, № 679, 683.
| ||||
|
| § 20, № 687, 689, 692, 694
| ||||
| 102 – 106 | Теорема Виета. | 5 |
| § 21, вопросы 1 – 4, № 708, 710, 712, | |
|
| § 21, № 714, 716, 718
| ||||
|
| § 21, № 723, 726, 728.
| ||||
|
| § 21, № 730, 732, 734, 736.
| ||||
|
| § 21, № 738, 741, 744.
| ||||
| 107 | Контрольная работа № 5 по теме «Квадратные уравнения. Теорема Виета» | 1 |
| § 19 – 21. | |
| 108 – 112 | Квадратный трехчлен. | 5 |
| § 22, вопросы 1 – 7, № 754 (1, 3, 5, 7, 9), 769, 770. | |
|
| § 22, № 754 (2, 4, 6, 8), 756, 771. | ||||
|
| § 22, № , 758, 760.
| ||||
|
| § 22, № 762, 764.
| ||||
|
| § 22, № 766, 768.
| ||||
| 113 – 119 | Решение уравнений, сводящихся к квадратным уравнениям. | 7 |
| § 23, вопрос 1, № 776 (1, 3, 5), 778 (1, 3, 5, 7), 780 (1). | |
|
| § 23, № 776 (2, 4, 6), 778 (2, 4, 6, 8), 780 (2). | ||||
|
| § 23, № 782, 784, 786.
| ||||
|
| § 23, № 788 (1 – 3), 790, 792 (1).
| ||||
|
| § 23, № 788 (1 – 4), 792 (2), 795 (1, 3). | ||||
|
| § 23, № 795 (2, 4), 798, 800. «Когда сделаны уроки», с. 191 – 192. | ||||
|
| § 23, № 164 – 169 (вариант 3, дидактические материалы, с. 83 – 84). | ||||
| 120 – 126 | Рациональные уравнения как математические модели реальных ситуаций. | 7 |
| § 24, № 804, 806, 834.
| |
|
| § 24, № 809, 811, 832.
| ||||
|
| § 24, № 813, 816, 833.
| ||||
|
| § 24, № 818, 820, 834.
| ||||
|
| § 24, № 823, 825, 835.
| ||||
|
| § 24, № 828, 830, 836, 837.
| ||||
|
| § 24, № 170 – 180 (вариант 3, дидактические материалы, с. 85 – 86). | ||||
| 127 | Повторение и систематизация учебного материала по теме «Квадратные уравнения». | 1 |
| § 22 – 24, задание № 6 «Проверьте себя» в тестовой форме, с. 202 – 203. | |
| 128 | Контрольная работа № 6 по теме «Квадратные уравнения» | 1 |
| § 22 – 24. | |
| Повторение и систематизация учебного материала – 8 часов | |||||
| 129 – 130 | Повторение по теме «Рациональные выражения». | 2 |
|
| № 841 (2, 4), 843 (2, 4, 6, 8, 10, 12), 848 (2, 4, 6), 849 (2, 4). |
|
| № 850 (2, 4, 6), 859 (2, 4, 6), 862 (2, 4, 6), 867 (2, 4, 6). | ||||
| 131 – 132 | Повторение по теме «Квадратные корни». | 2
|
|
| № 888 (2, 4), 889 (2, 4,6), 890(2, 4, 6, 8). |
|
| № 891(2, 4), 893 (2, 4, 6), 904(2, 4, 6), 905 (2, 4, 6), 908(2). | ||||
| 133 – 135 | Повторение по теме «Квадратные уравнения». | 3 |
|
| № 918 (2, 4, 6), 919 (2, 4), 921 (2, 4), 922 (2). |
|
| № 923 (2), 925, 927, 928.
| ||||
|
| № 930 (2, 4, 6, 8), 931 (2, 4), 938.
| ||||
| 136 | Итоговая административная контрольная работа | 1 |
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход


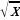 .
.








 Рабочая программа алгебра 8 класс (63.64 KB)
Рабочая программа алгебра 8 класс (63.64 KB)
 0
0 549
549 16
16 Нравится
0
Нравится
0




