1. Даны точки А(4;2), В(5;-1). Найти координаты середины отрезка АВ.
a) (0,5;4,5);
b) (4,5;0,5);
c) (9;1).
2. АВСD – параллелограмм. А(4;3), В(2;8), С(0;6) . Найти координаты середины диагонали АС.
a) (3; 8);
b) (2; 4,5);
c) (4,5; 2).
3. Дан треугольник АВС. А( 1;6), В( 4;8), С(4;-2). Найти длину медианы АК, где К-середина стороны ВС.
a) 10;
b) 5;
c) 3√2;
4. Найти координаты середины медианы РD треугольника МРК, если М(0;5), Р(4;2), К(6;-4).
a) (3,5; 1,25);
b) (1,25; 3,5);
c) (3; 0,5).

5. В окружности с центром N проведён диаметр MK. Найти координаты центра окружности и её радиус, если М(-3;0), К(3;0).
a) (2;2) и 4;
b) (0;0) и 3;
c) (0;3) и 3.
6. В параллелограмме МNPK, М(-3;0), N(0;3), P(6;3), K(3;0).
Найти координаты середины отрезка NО, если О - точка пересечения диагоналей параллелограмма.
a) (1,5; 4);
b) (0,75; 2,25);
c) (2,25; 0,75).
7. Даны точки A и В. А(3;4), В (-4;2). Найти длину вектора АВ.
a) 53;
b) 49;
c) √53.
8. Четырёхугольник АВСD задан координатами своих вершин А(-2;-3), В( -2;3), С(2;3), D( 2;-3). Найти периметр данного четырёхугольника.
a) 12
b) 8
c) 20.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


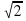 ;
;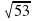 .
.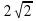 .
.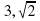 , 8
, 8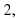 3, 1.
3, 1.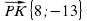 ,
,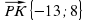
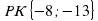 .
.








 Простейшие задачи в координатах (16.57 КB)
Простейшие задачи в координатах (16.57 КB)
 1
1 6221
6221 628
628 Нравится
0
Нравится
0



