Общая характеристика выбора раздела факультативного занятия.
Одним из видов задач по стереометрии являются задачи на нахождение углов:
- между 2 прямыми;
- между прямой и плоскостью;
- между 2 плоскостями.
Как показывает практика, решение этих задач нередко сопряжено с рядом трудностей.
В частности, основными проблемами для учащихся являются построение на чертеже искомого угла и доказательство того, что именно этот угол искомый.
Избежать подобных трудностей помогает координатно-векторный метод. Его главным преимуществом является то, что построение искомого угла не требуется.
Метод заключается во введении системы координат, определении координат вершин многогранников, а затем – определении углов между нужными векторами. Недостаток метода состоит в том, что при его использовании учащимся не всегда хватает знаний. Но этот недостаток легко устраним в старших классах.
В методе координат главная нагрузка приходится на алгебраические выкладки, однако, их целесообразность базируется на наглядном осмыслении задачи. Как показывает практика, этот метод доступен учащимся даже с недостаточно развитым пространственным воображением, что позволяет повысить уровень их подготовки к ЕГЭ.
Надо отметить, что координатным методом разумно пользоваться в задачах, решение которых вызывает затруднение при применении обычного метода, сводящего стереометрическую задачу к ряду планиметрических.
Метод координат – большая и важная тема школьного курса геометрии.
Изучение темы в 11 классе накладывается на уже известный материал, изученный в 9 классе.
Учащиеся имеют определенный опыт, владеют достаточным запасом математических понятий и умений.

При изучении темы мы формируем умение решать простейшие задачи в координатах, используя формулы для вычисления координат вектора, длины вектора, координат середины отрезка.
Изучение скалярного произведения векторов позволяет решать более сложные и интересные задачи:
- вычислять углы;
- находить расстояние.
Мы развиваем графическую культуру учащихся, пространственное воображение.
Выбор этого раздела не случаен, он позволяет реализовывать:
- основные принципы педагогических технологий;
- различные типы уроков;
- разные формы контроля знаний.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход



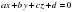 ;
;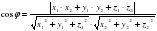 ;
; 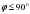

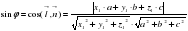
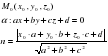










 Разработка факультативных занятий по математике по теме "Метод координат. Углы в пространстве" (0.34 MB)
Разработка факультативных занятий по математике по теме "Метод координат. Углы в пространстве" (0.34 MB)
 0
0 517
517 15
15 Нравится
0
Нравится
0


