"Производная: геометрический и физический смысл"

Геометрический и

физический смысл

производной

Начала математического анализа

Найдите производную функции f в точке x=2 .

f(x) = 5х − 6x 3

f ' (x) = 5 − 18x 2

f ' (2) = 5 − 18*2 2 = - 67

Лейбниц (1646-1716)

пришёл к понятию производной,

решая задачу проведения касательной к производной линии,

объяснив этим ее

геометрический смысл.

I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Касательная к кривой

Касательная

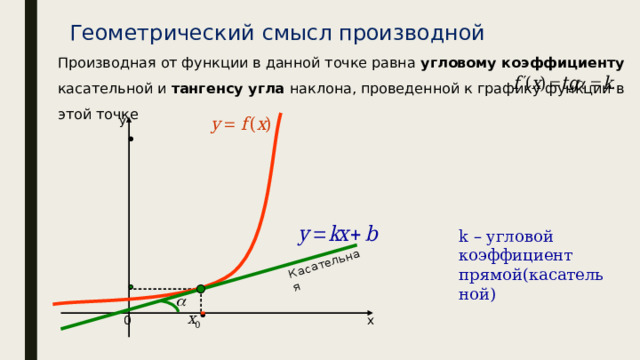
Геометрический смысл производной

Производная от функции в данной точке равна угловому коэффициенту касательной и тангенсу угла наклона, проведенной к графику функции в этой точке

y

k – угловой коэффициент прямой(касательной)

0

х

Алгоритм нахождения углового коэффициента/тангенса

угла наклона касательной в точке

1) Найти производную f’( х ).

2) Найти значение производной в точке х 0 : f’( х 0 ).

3) Записать ответ k = f’( х 0 ) или tgα = f’( х 0 ).

5

Рассмотрим примеры:

1) Найти угловой коэффициент касательной функции в заданной точке, k-?

2) Найти тангенс угла наклона касательной к графику функции в точке, tgα-?

5

Физический смысл производной

Физический смысл производной состоит в том, что производная функции в точке показывает скорость изменения функции в этой точке.

Пусть S(t) – функция, задающая зависимость от времени t, тогда:

v =S’(t)

А вторая производная функции показывает ускорение в момент времени:

a (t) = V’(t) = S’’(t)

Алгоритм нахождения скорости в момент времени

1) Найти производную S’( t ).

2) Найти значение производной в точке t 0 : S’( t 0 ).

3) Записать ответ v = S’( t 0 ).

5

Алгоритм нахождения ускорения в момент времени

1) Найти производную S’( t ).

2) Найти производную v’(t).

3) Найти значение производной в точке t 0 : v’( t 0 ).

4) Записать ответ a (t) = v’(t 0 ).

5

Рассмотрим примеры:

3) Найти скорость движущегося тела в момент времени , v - ?

4) Найти ускорение движущегося тела в момент времени , a -?

5

Касательная к графику функции

Зная уравнение функции и абсциссу точки касания х 0 , можно, составить уравнение этой касательной.

Уравнение касательной:

.

5

Алгоритм составления уравнения касательной

функции f(х) в точке

1) Найти значение функции в точке х 0 : f( х 0 ).

2) Найти производную: f’( х ).

3) Найти значение производной в точке х 0 : f’( х 0 ).

4) Записать уравнение касательной, подставив свои данные

5

Пример

Составьте уравнение касательной к графику функции в точке с абсциссой .

Уравнение касательной к графику функции в точке

Решение:

;

,

;

;

;

.

Ответ: .

1 команда 2 команда

Задание № 1

Задание № 1

Найдите тангенс угла наклона касательной к графику функции в точке

Найти угловой коэффициент касательной функции

в точке ?

Задание № 2

Задание № 2

Точка движется по закону

s. Найдите скорость точки в момент времени.

1 команда 2 команда

Задание № 1

Задание № 1

Ответ: 1

Ответ: 4

Задание № 2

Задание № 2

Ответ: 60

Ответ: 22

Рефлексия

Выберите один вариант и продолжите

• сегодня я узнал… 
•   было интересно… 
•   было трудно… 
•   я выполнял задания… 
•   я понял, что… 
•   теперь я могу… 
•   я почувствовал, что… 

• я приобрел… 
•   я научился… 
• у меня получилось … 
• я смог… 
•   я попробую… 
• меня удивило…

«Вы ещё очень мало знаете, но у Вас

положительная производная.

Скорость приращения Ваших знаний возрастает,

а это и есть залог того, что ваши знания

будут максимальны».