Муниципальное автономное общеобразовательное учреждение
гимназия № 26
СОГЛАСОВАНО УТВЕРЖДАЮ:
на заседании научно-методического Директор муниципального автономного
совета МАОУ гимназии № 26 общеобразовательного учреждения
гимназии № 26
Протокол № 1 от ___ августа 2014г. Протокол № ____ от ___ августа 2014г.
___________Р.И. Набатова ___________ И.Э.Кашенова
ПРОГРАММА
ОБРАЗОВАТЕЛЬНОГО КУРСА ПО МАТЕМАТИКЕ
«Избранные вопросы математики»
10-11 классы
(модифицированная)
Автор:
Наумова Марина Ивановна, учитель математики
Томск 2014
Пояснительная записка
Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, связанная с мышлением человека, с овладением определенным методом познания и преобразования мира математическим методом.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Использование в математике наряду с естественным нескольких математических языков дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в ее современном толковании является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. История развития математического знания дает возможность пополнить запасы историко–научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:
- овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
- формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
- формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи расширенное и углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Занятия курса призваны помочь ученику осознать степень своего интереса к предмету и оценить возможности овладения им, с тем, чтобы он смог сделать сознательный выбор в пользу дальнейшего углубленного либо обычного изучения математики. Интерес и склонности учащегося к математике должны всемерно подкрепляться и развиваться. Учащиеся должны приобрести умения решать задачи более высокой сложности, точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач и доказательствах теорем, правильно пользоваться математической терминологией и символикой, применять рациональные приемы вычислений и тождественных преобразований, использовать наиболее употребительные эвристические приемы и т.д.
В программу включены ряд дополнительных вопросов, непосредственно примыкающих к курсу алгебры и начал анализа, к его основным идейным линиям. Включены также самостоятельные разделы, которые в настоящее время не изучаются, но являются важными содержательными компонентами системы непрерывного математического образования.
Включение дополнительных вопросов преследует две цели:
- создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике;
- восполнение содержательных пробелов основного курса, придающее содержанию изучения необходимую целостность.
Изучение математики предполагает наполнение курса разнообразными, интересными и сложными задачами, овладение основным программным материалом на более высоком уровне.
Для поддержания и развития интереса к предмету в программу включены занимательные задачи, сведения из истории математики.
Программа составлена на основе изучения курса алгебры и начал анализа по учебнику «Алгебра и начала анализа: учебник для 10, 11 кл. общеобразовательных учреждений / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]. – М.: Просвещение, 2012.
Цель программы:
Задачи программы:
формировать у учащихся сознательное и прочное овладение системой математических знаний, умений, навыков;
систематизировать знания по алгебре и началам анализа; детально расширить темы, недостаточно глубоко изучаемые в школьном курсе и, как правило, вызывающие затруднения у учащихся;
развивать математические способности учащихся;
способствовать вовлечению учащихся в самостоятельную исследовательскую и проектную деятельность.
Класс универсальный.
Срок реализации программы 2 года.
Содержание программы
10 класс
|
Название раздела, темы
|
Теоретический раздел программы |
|
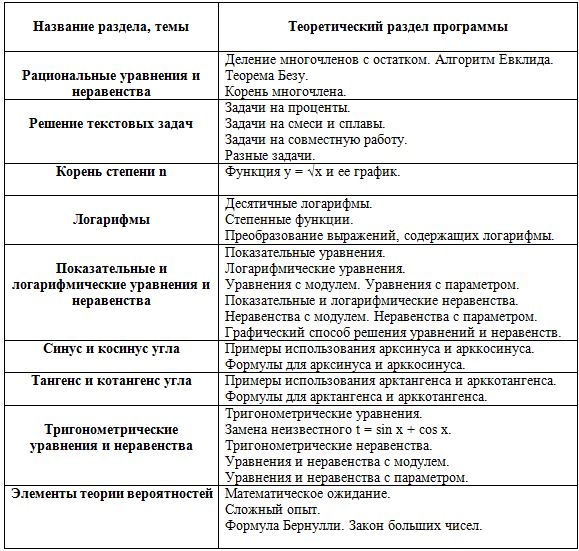
Рациональные уравнения и неравенства | Деление многочленов с остатком. Алгоритм Евклида. Теорема Безу. Корень многочлена. |
|
Решение текстовых задач | Задачи на проценты. Задачи на смеси и сплавы. Задачи на совместную работу. Разные задачи. |
| Корень степени n
| Функция у = √х и ее график.
|
|
Логарифмы
| Десятичные логарифмы. Степенные функции. Преобразование выражений, содержащих логарифмы. |
|
Показательные и логарифмические уравнения и неравенства | Показательные уравнения. Логарифмические уравнения. Уравнения с модулем. Уравнения с параметром. Показательные и логарифмические неравенства. Неравенства с модулем. Неравенства с параметром. Графический способ решения уравнений и неравенств. |
| Синус и косинус угла | Примеры использования арксинуса и арккосинуса. Формулы для арксинуса и арккосинуса. |
| Тангенс и котангенс угла | Примеры использования арктангенса и арккотангенса. Формулы для арктангенса и арккотангенса. |
|
Тригонометрические уравнения и неравенства | Тригонометрические уравнения. Замена неизвестного t = sin x + cos x. Тригонометрические неравенства. Уравнения и неравенства с модулем. Уравнения и неравенства с параметром. |
| Элементы теории вероятностей
| Математическое ожидание. Сложный опыт. Формула Бернулли. Закон больших чисел.
|
Содержание программы
11 класс
|
Название раздела, темы
|
Теоретический раздел программы |
| Функции и их графики | Основные способы преобразования графиков. Графики функций, связанных с модулем. Графики сложных функций. Разрывные функции. |
| Производная | Непрерывность функций, имеющих производную. Дифференциал. Производная сложных функций. Производная обратной функции. |
| Применение производной | Теоремы о среднем. Производные высших порядков. Выпуклость и вогнутость графика функции. Асимптота. Формула и ряд Тейлора. |
| Первообразная и интеграл | Замена переменной. Интегрирование по частям. Применение определенных интегралов в геометрических и физических задачах. Понятие дифференциального уравнения. Задачи, приводящие к дифференциальным уравнениям. |
| Уравнения. Неравенства. Системы. Нестандартные методы решения уравнений и неравенств | Уравнения с дополнительными условиями. Неравенства с дополнительными условиями. Уравнения и неравенства с модулями. Метод интервалов для непрерывных функций. Использование областей существования функций. Использование неотрицательности функций. Использование ограниченности функций. Использование свойств синуса и косинуса. Использование числовых неравенств. Использование производной для решения уравнений и неравенств. Уравнения с параметром. Неравенства с параметром. |
Учебно-тематический план
10 класс
|
Наименование раздела, темы
|
Количество часов по теме |
| Рациональные уравнения. Неравенства. Деление многочленов с остатком. Алгоритм Евклида. Теорема Безу. Корень многочлена. | 3/6 1/2 1/2 1/2 |
| Решение текстовых задач. Задачи на проценты. Задачи на смеси и сплавы. Задачи на совместную работу. Разные задачи. | 6/12 1/2 1/2 1/2 2/4 |
| Корень степени n. Функция у = √х и ее график. | 2/4 2/4 |
| Логарифмы. Десятичные логарифмы. Степенные функции. Преобразование выражений, содержащих логарифмы. | 2/4 1/2 1/2 4/8 |
| Показательные и логарифмические уравнения и неравенства. Показательные уравнения. Логарифмические уравнения. Уравнения с модулем. Уравнения с параметром. Показательные и логарифмические неравенства. Неравенства с модулем. Неравенства с параметром. Графический способ решения уравнений и неравенств. |
6/12 1/2 1/2 1/2 1/2 1/2 1/2 |
| Синус и косинус угла. Примеры использования арксинуса и арккосинуса. Формулы для арксинуса и арккосинуса. | 2/4 1/2 1/2 |
| Тангенс и котангенс угла. Примеры использования арктангенса и арккотангенса. Формулы для арктангенса и арккотангенса. | 2/4 1/2 1/2 |
| Тригонометрические уравнения и неравенства. Тригонометрические уравнения. Замена неизвестного t = sin x + cos x. Тригонометрические неравенства. Уравнения и неравенства с модулем. Уравнения и неравенства с параметром. | 5/10 1/2 1/2 1/2 1/2 1/2 |
| Элементы теории вероятностей. Математическое ожидание. Сложный опыт. Формула Бернулли. Закон больших чисел.
| 3/6 1/2 1/2 1/2 |
| Итого | 34 часов/68 часов |
Учебно-тематический план
11 класс
|
Название раздела, темы
|
Количество часов по теме |
| Функции и их графики Основные способы преобразования графиков Графики функций, связанных с модулем Графики сложных функций Разрывные функции Решение заданий по теме из КИМов ЕГЭ | 5/10 1/2 1/2 1/2 1/2 1/2 |
| Производная Непрерывность функций, имеющих производную Дифференциал. Дифференциальные уравнения Производная сложных функций Производная обратной функции Решение заданий по теме из КИМов ЕГЭ | 5/10 1/2 1/2 1/2 1/2 1/2 |
| Применение производной Теоремы о среднем Производные высших порядков Выпуклость и вогнутость графика функции. Асимптота Формула и ряд Тейлора Решение заданий по теме из КИМов ЕГЭ | 5/10 1/2 1/2 1/2 1/2 1/2 |
| Первообразная и интеграл Замена переменной Интегрирование по частям Применение определенных интегралов в геометрических и физических задачах Понятие дифференциального уравнения Задачи, приводящие к дифференциальным уравнениям Решение заданий по теме из КИМов ЕГЭ | 6/12 1/2 1/2 1/2
1/2 1/2 1/2 |
| Уравнения. Неравенства. Системы. Нестандартные методы решения уравнений и неравенств Уравнения с дополнительными условиями Неравенства с дополнительными условиями Уравнения и неравенства с модулями Метод интервалов для непрерывных функций Использование областей существования функций Использование неотрицательности функций Использование ограниченности функций Использование свойств синуса и косинуса Использование числовых неравенств Использование производной для решения уравнений и неравенств Уравнения с параметром Неравенства с параметром Решение заданий по теме из КИМов ЕГЭ |
13/26 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2 |
| Итого | 34 часа/68 часов |
Требования к математической подготовке учащихся
В результате изучения данного курса учащиеся должны
знать:
основные приемы решений рациональных, иррациональных, показательных, логарифмических, тригонометрических уравнений, неравенств и их систем
правила преобразований выражений, графиков функций
способы решения текстовых и других задач
четко основные определения, формулы и свойства
уметь:
выполнять тождественные преобразования рациональных, логарифмических, тригонометрических и других выражений
строить графики элементарных и более сложных функций
решать задачи, уравнения, неравенства, системы, предусмотренные программой курса
применять аппарат математического анализа к решению задач.
Формы, методы, способы и средства реализации программы
привлечение учащихся к составлению таблиц, графиков, изготовлению наглядного, дидактического, раздаточного материала, подготовке презентаций
использование на занятиях игровых моментов: конкурсов, математических боев, КВН и др.
изучение, конспектирование учащимися материала из дополнительной литературы
использование компьютерных, тестовых и других технологий.
Учебно- методическое обеспечение программы
специальная справочная литература
методическая литература
дидактический и раздаточный материал
набор КИМов ЕГЭ прошлых лет
Список литературы по программе
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. Алгебраический тренажер. «Илекса» «Гимназия», Москва-Харьков, 1998.
Р.Б.Райхмист. Графики функций. Задачи и упражнения. «Школа-пресс», Москва, 1997.
Г.А.Ястребинецкий. Уравнения и неравенства с параметрами. «Просвещение», Москва, 1972.
И.Т.Бородуля. Тригонометрические уравнения и неравенства. «Просвещение», Москва, 1998.
А.П.Ершова, В.В.Голобородько. Самостоятельные и контрольные работы. Алгебра и начала анализа. 10-11 кл. Разноуровневые дидактические материалы.
С.В.Кравцов и др. Методы решения задач по алгебре: от простых до самых сложных.
М.И.Шабунин. Математика для поступающих в ВУЗы. Уравнения и системы уравнений.
М.И.Шабунин. Математика для поступающих в ВУЗы. Неравенства и системы неравенств.
В.А.Гольдич. Алгебра. Решение уравнений и неравенств. Школьная программа.
В.Г.Брагин, А.И.Грабовский. Все предметы школьной программы в схемах и таблицах. Алгебра. Геометрия.
В.С.Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа, «Просвещение», 1990.
В.С.Крамор, А.А.Михайлов. Тригонометрические функции, «Просвещение», 1983.
А.Мерзляк и др. Тригонометрия. Задачник к школьному курсу. 8-11 кл. «АСТ-ПРЕСС: Магистр-S», 1998.
Л.О.Денищева и др. Учимся решать уравнения и неравенства. 10-11кл.
М.И.Башмаков и др. Задачи по математике. Алгебра и анализ.
Б.Г.Зив. Тесты по алгебре и началам анализа. 10-11кл.
Р.Д.Лукин и др. Устные упражнения по алгебре и началам анализа..
Г.Г.Левитас. Карточки для коррекции знаний по алгебре. 10-11кл.
Е.С.Канин и др. Упражнения по началам математического анализа в 10-11кл.
И.Т.Бородуля. Показательная и логарифмическая функции (задачи и упражнения).

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа образовательного курса по математике "Избранные вопросы математики 10-11 классы" (90.5 КB)
Программа образовательного курса по математике "Избранные вопросы математики 10-11 классы" (90.5 КB)
 0
0 1409
1409 139
139 Нравится
0
Нравится
0


