Программирование итерационных процессов

Тема 2

Разработка программ с циклами Лекция 2.1.

Программирование итерационных процессов.

Литература

Основная:

Подбельский В.В., Фомин С.С. Программирование на языке Си: Учеб. пособие. – М.: Финансы и статистика, 2004.

Дополнительная:

С/ C ++ Структурное программирование. Практикум. Программирование на языке высокого уровня. Питер, 2004.

Юркин А. Задачник по программированию. Гриф МО. Учебное пособие, Питер, 2002.

Шмидт Г. Самоучитель Си++. СПб.: БХВ – Петербург, 2004.

Вопросы:

1. Погрешности обработки данных.

2. Преобразование математических формул к виду, удобному для программирования.

3. Итерационные циклы.

1. Погрешности обработки данных

Абсолютная и относительная ошибки

Абсолютная ошибка величины есть разница между истинным значением и значением, измеренным или вычисленным.

Относительная ошибка определяется как частное от деления абсолютной ошибки на истинное значение.

Истинное значение неизвестно, поэтому оно «заменяется» измеренным или вычисленным значением.

Пусть:

х - точное значение,

х * - измеренное или вычисленное значение.

Абсолютная ошибка  х = х - х * .

Относительная ошибка  х = ( х - х * )/ х.

Если бы точное значение ошибки было известно, то истинное значение числа было бы также известно, и анализ ошибок был бы не нужен.

Обычно истинное значение неизвестно, поэтому ошибку оценивают по ее максимальному значению или по вероятности того, что она не превысит некоторой величины.

Ошибки накапливаются в процессе вычислений и распространяются по-разному для различных математических операций. Важно знать, как ошибки влияют на конечные результаты, т. е. как много значащих цифр будет иметь результат на выходе ЭВМ.

В числовых расчетах имеется три основных источника ошибок:

- исходная ошибка,

- ошибка усечения,

- ошибка округления.

Исходные ошибки – это ошибки в значениях исходных данных. Они вызваны неопределенностью измерений из-за природы физических величин или погрешностью измерительной аппаратуры, а также небрежностью пользователей и программистов (например, вместо π числа используют приближенное значение 3.14).

Некоторые величины и многие рациональные дроби нельзя представить конечным набором десятичных цифр. Примерами таких величин являются корень из двух , числа е ,  , простая дробь 1/3 .

В двоичной системе счисления многие конечные десятичные дроби имеют бесконечное двоичное представление. Например 1/10 в двоичном виде

0.000110011001100...

В двоичной арифметике, использующей конечное число битов, 10 (10) * 0.1 (10) никогда не будет равно точно 1.

Бесконечное двоичное представление конечных десятичных чисел может привести к «неправильному» результату сравнения величин (например, при проверке на нуль).

Ошибки усечения вносят численные процедуры. Часто математические определения содержат бесконечность. Например, функция е х представима бесконечным рядом

Ряд сходится при любом х.

По очевидным причинам нельзя использовать все члены ряда. Сложение заканчивается после вычисления некоторого конечного числа членов . Опущенные члены (их количество бесконечно) вносят ошибку в результат, которая называется ошибкой усечения.

В ряде случаев максимальную абсолютную ошибку усечения можно оценить математически. Для сходящегося знакопеременного ряда она меньше, чем модуль первого отброшенного члена ряда.

Ошибка округления . ЭВМ оперируют с конечным числом цифр в представлении числа. Даже при выполнении простых арифметических действий возникают ошибки - ошибки округления. Предположим, что ЭВМ может запоминать только числа, состоящие из четырех цифр, и пусть необходимо сложить два числа 23.45 и 4.567, каждое из которых рассматривается как точное. Сумма этих чисел равняется 28.017 и состоит из пяти цифр, для сохранения в памяти ЭВМ результат следует округлить .

Способы округления

1. Значащие цифры, не умещающиеся в участок памяти, отбрасываются.

2. Лишние цифры отбрасываются, но последняя цифра числа увеличивается на 1, если первая цифра отброшенной части ≥ 0.5 в десятичной арифметике (в арифметике с основанием А , если ≥ 0.5 А ). Это симметричное округление.

Уменьшение ошибок В алгебре справедливы законы коммутативности и дистрибутивности. В машинной арифметике из-за ошибок округления существен порядок, в котором выполняются операции. Рассмотрим пример сложения 4 х -разрядных десятичных чисел с плавающей точкой 0.6000*10 0 0.7000*10 0 0.1000*10 4 Правильный результат 0. 10 013 *10 4 , или 0.10 01 *10 4 =1001, если выполнить округление до четырех значащих цифр. Если производить суммирование сверху вниз, то машина получит правильный результат при симметричном округлении до 4 х цифр на каждом шаге суммирования. Если проводить сложение снизу вверх, то получится неправильный результат 0.1002 *10 4 =1002

Округления на каждом этапе сложения искажают результат. Чем их больше, тем больше будет разница. Поэтому при сложении и вычитании желательно начинать обрабатывать меньшие числа или числа одного порядка. Может показаться, что излишне беспокоиться по поводу небольших ошибок. Но вычислительные процессы могут требовать сотен или тысяч операций, и постепенно малая ошибка значительно увеличивается за счет ее повторения или за счет ее распространения и влияния на более поздние этапы вычислений.

Большие абсолютные ошибки могут возникать при вычитании двух почти равных чисел, каждое из которых подвержено ошибкам округления, усечения или исходной ошибке. Если рассматривать два точных числа 1590.5 и 1590.4, то разность их 4 х -разрядного представления будет

1591 - 1590 = 0001,

что в 10 раз отличается от правильного результата. В этом случае даже первые цифры результата содержат ошибку. Если такое вычитание выполняется на промежуточном шаге вычисления, то эта ошибка повлияет на дальнейшие вычисления и приведет к неправильным результатам.

void main()

{

float a,b,y,y1;

a= 1 0.95;

b=0.001;

y=(a+b)*(a+b);

y1= - a*a-2.0*a*b;

y1=(y+y1)/b/b;

printf(“\ny1=%f”,y1); //рез-тат равен 1 ?

}

2. Преобразование математических формул к виду, удобному для программирования

y = y 1 - y 2 + y 3 - …

Очередной i +1 член ряда y i +1 формируется на основе предыдущего y i по простому соотношению y i +1 = y i * R i + 1 .

Значение R i + 1 определяется путем деления y i +1 / y i .

Для данного ряда R i + 1 = - x /( i +1).

 , то переход к п.2 6. Конец. " width="640"

Алгоритм вычисления ряда

1. Установка начальных значений:

y = x ; y i = x ; i = 1 .

2. Переход к очередному члену ряда

i = i + 1 .

3. Вычисление очередного члена ряда

y i = y i R i + 1 = - y i *х / i .

4. Суммирование

y = y + y i .

5. Если | y i |  , то переход к п.2

6. Конец.

3. Итерационные циклы

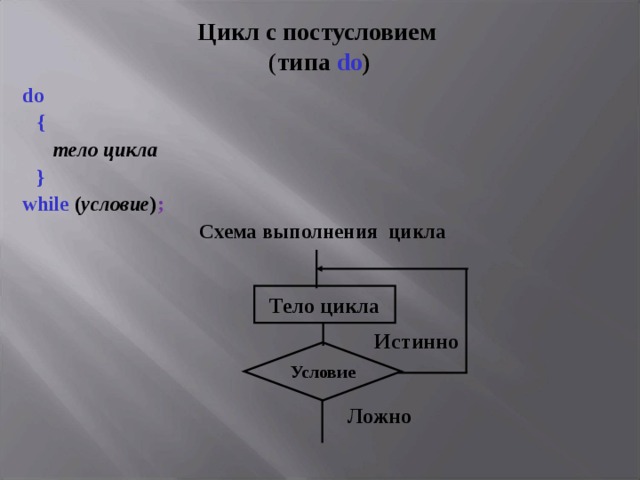
Цикл с постусловием ( типа do )

do

{

тело цикла

}

while ( условие ) ;

Схема выполнения цикла

Тело цикла

Истинно

Условие

Ложно

delta ) ); " width="640"

Фрагмент программы с использованием цикла do

y=x; i=1; yi=x;

do

{

i++; // i=i+1;

yi=–yi*x/i;

y=y+yi;

}

while ( (yi -delta ) || ( yi delta ) );

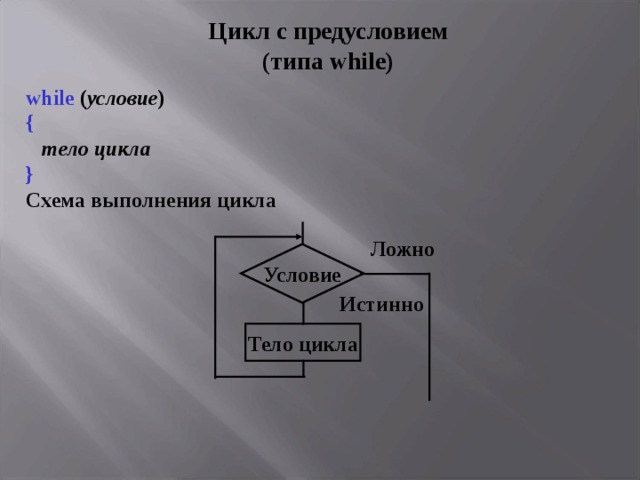
Ц икл с предусловием (типа while )

while ( условие )

{

тело цикла

}

Схема выполнения цикла

Ложно

Условие

Истинно

Тело цикла

delta) { i++; yi*=–x/i; // yi=yi*(–x/i); y+=yi; // y=y+yi; } " width="640"

Фрагмент программы с использованием цикла while

#include

. . .

y=x; i=1; yi=x;

while (fabs(yi) delta)

{

i++;

yi*=–x/i; // yi=yi*(–x/i);

y+=yi; // y=y+yi;

}

ε , то возврат к п.2. Иначе переход к п.4. Здесь ε заданная погрешность вычисления. 4. Конец. " width="640"

Нахождение корня нелинейного уравнения F ( x ) = 0

методом итераций

Предварительно уравнение следует преобразовать к виду

x = f ( x )

и получить выражение для производной f ‘ ( х ) .

Этапы вычисления корня

1. Задать начальное приближение x 0 .

2. Вычислить следующее приближение к корню

3. Если | x n – x n +1 | ε , то возврат к п.2. Иначе переход к п.4. Здесь ε заданная погрешность вычисления.

4. Конец.

0, k 1 , k – целая величина. Вместо величины x может стоять любое выражение f ( x ) . " width="640"

Вычисление корня k - й степени

методом итераций

при условиях x 0, k 1 , k – целая величина. Вместо величины x может стоять любое выражение f ( x ) .

Вопросы для самоподготовки

1. Виды и источники погрешностей в компьютерных вычислениях.

2. Различия математических и компьютерных вычислений.

3. Цели и сущность преобразования формул к виду, удобному для программирования.

4. Сущность этапов выполнения цикла типа do - while .

5. Сущность этапов выполнения цикла типа while .

6. Различия между циклами типа do - while и while .

0 . Для вычисления корня воспользоваться методом итераций. Гиперболический синус вычислить, используя ряд Значения погрешности итерационных вычислений, величины х и величины k задаются вводом. Отобразить: - значение корня, значение sh(x) , значение функции; - количество итераций, потребовавшихся на корня и sh(x) . Проверить правильность результатов выполнения программы расчетом контрольных точек в Excel . " width="640"

Практическое занятие Составление программ инженерных задач с итерационными вычислениями

Составить программу вычисления функции

,

где k равно 2 или 3; х 0 .

Для вычисления корня воспользоваться методом итераций.

Гиперболический синус вычислить, используя ряд

Значения погрешности итерационных вычислений, величины х и величины k задаются вводом.

Отобразить:

- значение корня, значение sh(x) , значение функции;

- количество итераций, потребовавшихся на корня и sh(x) .

Проверить правильность результатов выполнения программы расчетом контрольных точек в Excel .