Логические основы устройства компьютера

Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.

Схема И реализует конъюнкцию двух или более логических значений.

Единица на выходе схемы И будет тогда и только тогда,  когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

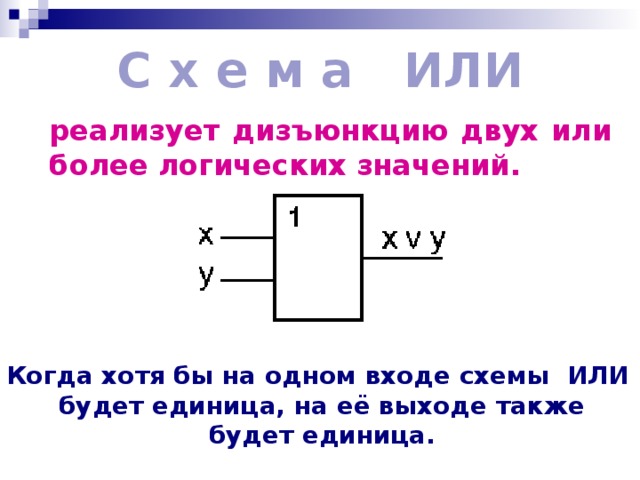
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.

Когда хотя бы на одном входе схемы  ИЛИ  будет единица, на её выходе также будет единица.

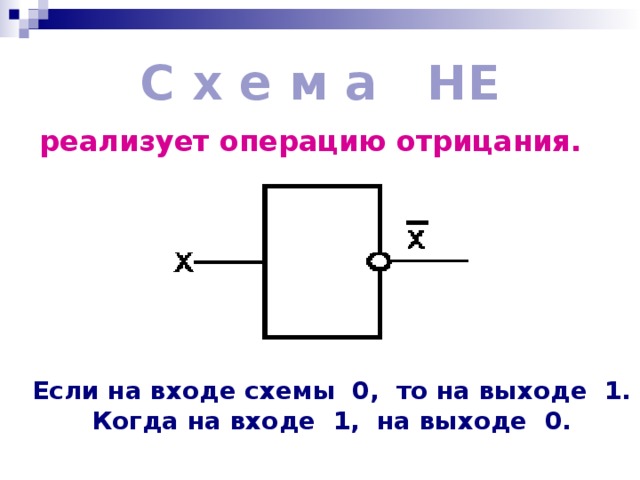
Схема НЕ реализует операцию отрицания.

Если на входе схемы  0,  то на выходе  1.  Когда на входе  1,  на выходе  0.

  Логические основы устройства компьютера

Логический элемент компьютера

— это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.

С х е м а   И

реализует конъюнкцию двух или более логических значений.

Единица на выходе схемы И будет тогда и только тогда,

когда на всех входах будут единицы.

Когда хотя бы на одном входе будет ноль,

на выходе также будет ноль.

С х е м а   ИЛИ

реализует дизъюнкцию двух или более логических значений.

Когда хотя бы на одном входе схемы  ИЛИ  

будет единица, на её выходе также

будет единица.

С х е м а   НЕ

реализует операцию отрицания. 

Если на входе схемы  0,  то на выходе  1. 

Когда на входе  1,  на выходе  0. 

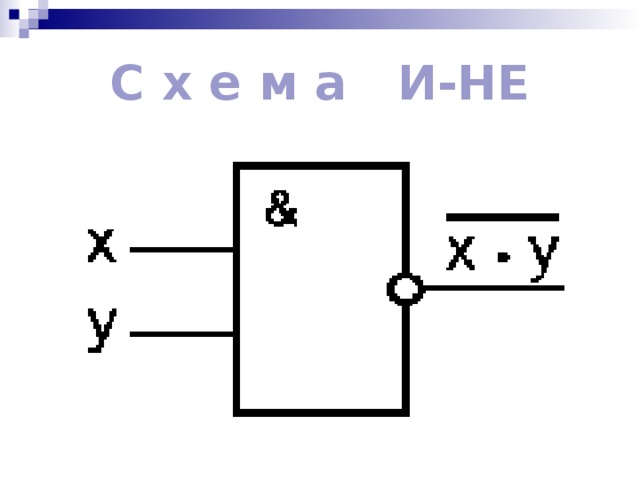
С х е м а   И-НЕ

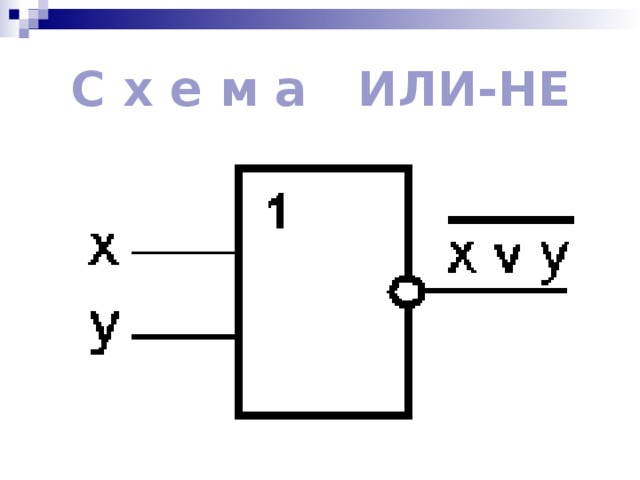
С х е м а   ИЛИ-НЕ

Значок инверсии

значок инверсии

Задача № 1

По заданной логической функции построить логическую схему

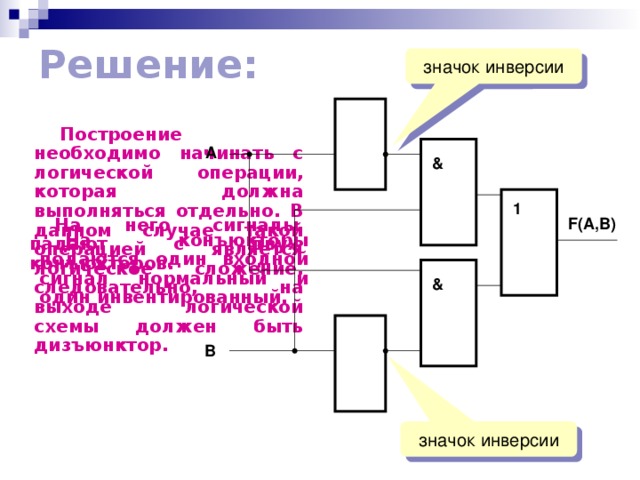
Решение:

значок инверсии

Построение необходимо начинать с логической операции, которая должна выполняться отдельно. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор.

А

&

1

На него сигналы падают с двух конъюкторов.

F(A,B)

На конъюкторы подаются один входной сигнал нормальный и один инвентированный.

&

В

значок инверсии

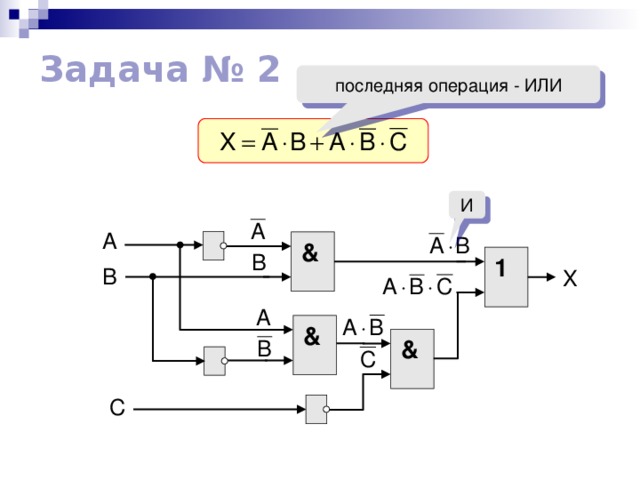
Задача № 2

последняя операция - ИЛИ

И

&

1

&

&

11

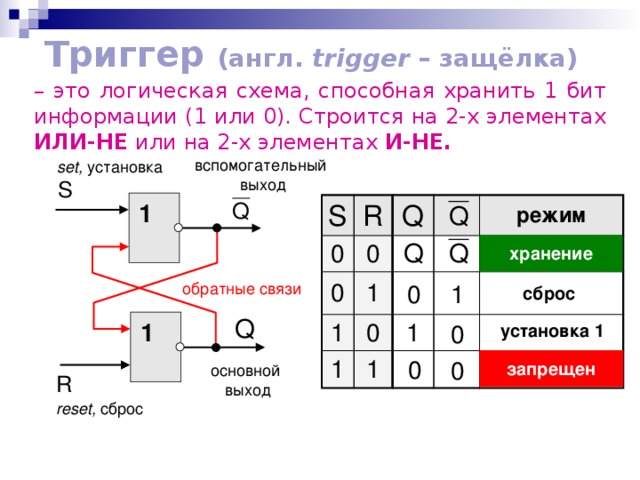
Триггер (англ. trigger – защёлка)

– это логическая схема, способная хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.

вспомогательный

выход

set, установка

1

S

R

0

Q

0

0

1

1

0

1

режим

1

хранение

0

обратные связи

сброс

1

установка 1

1

1

0

запрещен

0

0

основной

выход

reset, сброс

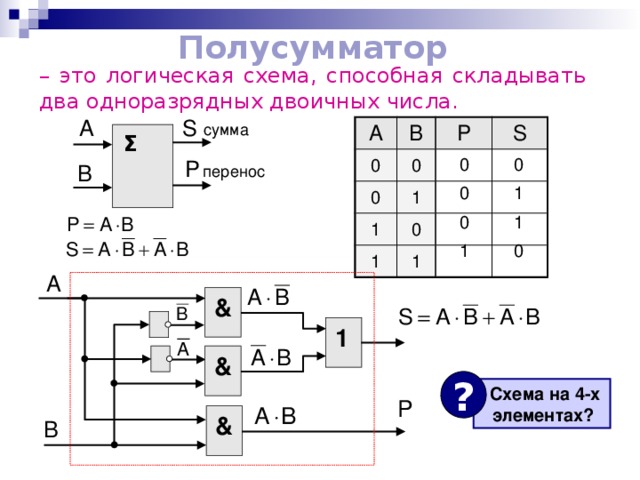
Полусумматор

– это логическая схема, способная складывать два одноразрядных двоичных числа.

сумма

A

B

0

0

0

P

S

1

1

0

1

1

Σ

0 0

перенос

0 1

0 1

1 0

&

1

&

?

Схема на 4-х элементах?

&

13

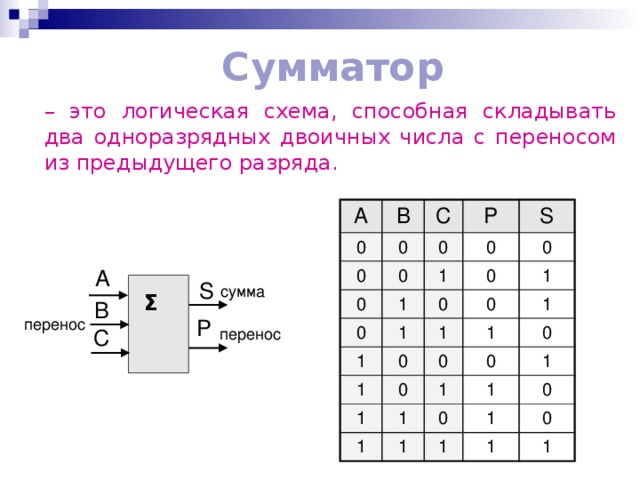
Сумматор

– это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего разряда.

A

B

0

0

0

C

0

P

0

0

0

S

1

1

0

1

0

0

0

1

0

1

0

1

1

0

1

1

1

0

1

1

1

0

0

1

1

0

1

1

1

0

1

0

1

сумма

Σ

перенос

перенос

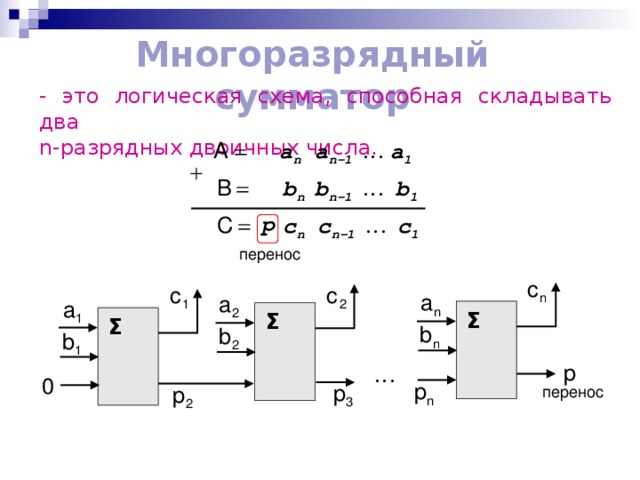
Многоразрядный сумматор

- это логическая схема, способная складывать два n-разрядных двоичных числа.

перенос

Σ

Σ

Σ

перенос

15