Прикладной курс «КОМБИНАТОРИКА»
Учитель математики Вал Екатерина Степановна
Занятие 1. Правило произведения
Цели занятия:
• дать понятие «кортеж»;
• познакомить учащихся с правилом произведения в комбинаторике;
• закрепить данное правило при решении задач.
Любой номер, составленный из трех цифр, нельзя рассматривать как множество из трех элементов, так как:
1) в номерах цифры могут повторяться (например, 775), а в множествах элементы не повторяются;
2) в номерах важен порядок цифр (175 и 571 — совсем разные номера), а в множествах порядок элементов роли не играет.
Поэтому при изучении таких объектов, как номера или слова (в них буквы могут повторяться, а от перестановки букв слово меняется), вводится новое математическое понятие «кортеж».
ОПРЕДЕЛЕНИЕ. Пусть имеется несколько множеств X1,…, Xk. Представим себе, что их элементы сложены в мешки, а мешки пронумерованы. Вытащим из первого мешка какой-нибудь элемент (то есть возьмем какой-нибудь элемент а1, множества Х1), затем вытащим элемент а2 из мешка Х2 и будем продолжать этот процесс до тех пор, пока из мешка Xk не будет вытащен элемент аk. После этого расставим полученные элементы в том порядке, в каком они появились из мешков (а1 , а2,.. аk ). Это и будет кортеж длины k, составленный из элементов X1, Х2,…, Xk. Элементы а1 , а2,.. аk называют компонентами кортежа.
Элементы кортежа могут повторяться, так как в определении не сказано, что элементы множеств X1, Х2,…, Xk не могут иметь одинаковых элементов.
ОПРЕДЕЛЕНИЕ. Два кортежа называют равными в том и только том случае, когда они имеют одинаковую длину, а на соответствующих местах стоят одни и те же элементы.
Примером кортежа длины 6 являются номера телефонов, они составлены из элементов множества X = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Слова русского языка (точнее, их запись) — кортежи различной длины, составленные из букв русского алфавита, а предложения — кортежи, составленные из русских слов.
Правило произведения. Если элемент а, можно выбрать п1 способами, после каждого выбора этого элемента следующий за ним элемент а2 можно выбрать п2 способами ... а после выбора элементов а1 , а2,.. аk-1, элемент ak выбирается nk способами, то кортеж (а1 , а2,.. аk) можно выбрать n1 • п2 •... • nk способами.
Задача 1. Из города А в город В ведут пять дорог, а из города В в город С — три дороги. Сколько путей, проходящих через В, ведут из А в С?
Решение. Каждый путь искомого вида задается кортежем (а1 , а2), где а1, — один из путей, соединяющих А и В, a а2 — один из путей, соединяющих В и С. Так как по условию а1 можно выбрать пятью способами, а а2 — тремя способами, то кортеж (а1, а2) можно по правилу произведения составить 5∙3 = 15 способами.
Ответ: 15 путей.
Задача 2. Сколькими способами можно выбрать гласную и согласную буквы слова «полка»?
Решение. В этом слове две гласные буквы (о, а) и три согласные (п, л, к). Каждый искомый выбор задается кортежем (а1, а2),где а1, — гласная буква, а а2 — согласная. Так как а1, можно выбрать двумя способами, а а2 — тремя способами, то кортеж (а1, а2) можно по правилу произведения выбрать 2∙3 = 6 способами.
Ответ: 6 способов.
Задача 3. Имеется шесть перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну на правую руку так, чтобы эти перчатки были различных размеров?
Решение. Эту задачу тоже можно решить по правилу произведения. Перчатка на левую руку может быть выбрана шестью способами. После того, как она выбрана, перчатку на правую руку можно выбрать лишь пятью способами (размеры перчаток должны быть разными). Поэтому всего имеет 6 • 5 = 30 способов.
Ответ: 30 способов.
Задача 4. Гера, Афина и Афродита попросили Париса не только назвать самую красивую из них, но и указать, кто на «втором и третьем местах». Сколько есть вариантов ответа?
Решение. Эту задачу также можно решать по правилу произведения. На первое место Парис может
выбрать тремя способами, на второе — двумя способами (одна претендентка уже находится на первом месте), на третье место — одним способом. Поэтому всего имеем 3 • 2 • 1 = 6 способов.
Ответ: 6 способов.
Задача 5. Сколькими способами могут быть распределены золотая и серебряная медали по итогам первенства по футболу, если число команд 12?
Решение. На золотую медаль претендуют 12 команд, на серебряную — 11 команд (одна получит золотую медаль). По правилу произведения получаем 12∙11 = 132 способа.
Ответ: 132 способа.
Задачи для домашней работы
1. Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?
2. На вершину горы ведут семь дорог. Сколькими способами турист может подняться на гору и потом спуститься с нее? Решите эту же задачу при дополнительном условии, что спуск и подъем происходят по разным дорогам.
3. Сколькими способами можно указать на шахматной доске два квадрата — белый и черный? Решите эту же задачу, если нет ограничений на цвет квадратов; если надо выбрать два белых квадрата.
Ответы: 1. 9. 2. 49; 42. 3. 1024; 4032; 992.
Дополнительные задачи
1. Десять участников конференции обменялись рукопожатиями, пожав каждый каждому руку. Сколько всего рукопожатий было сделано?
2. Сколько различных шифров можно набрать в автоматической камере хранения, если шифр составляется с помощью любой из тридцати букв русского алфавита с последующим трехзначным числом?
3. Сколько имеется семизначных натуральных чисел, в которых все цифры, стоящие на нечетных местах, различные?
4. Сколько различных танцевальных пар (юноша, девушка) можно составить из пяти юношей и восьми девушек?
5. На районную олимпиаду школа должна набрать команду из трех участников: одного из трех лучших надо выбрать для участия в олимпиаде по химии, одного из четырех — по физике, одного из семи — по математике. Сколькими способами можно составить такую команду?
6. Сколько различных трехзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр 1, 2 и 3? Сколькими способами можно составить расписание уроков на один день из шести разных учебных предметов?
7. Путешественник может попасть из пункта А в пункт С, проехав через пункт В. Между пунктами А и В имеется три автодороги. А между пунктами В и С — железнодорожное и речное сообщения. Сколько существует различных маршрутов между пунктами А и С?
8. В одной из стран автомобильные номера из четырех цифр (нуль не может стоять на первом месте) записываются на пластинках пяти различных цветов (каждый из пяти штатов этой страны имеет номера своего цвета). Сколько разных пластин с номерами может быть выдано автовладельцам в этой стране?
9. Десять участников конференции обменялись визитными карточками (каждый вручил свою карточку всем другим участникам). Сколько всего карточек было роздано?
10. Имеется восемь видов конвертов без марок и пять видов марок. Сколькими способами можно выбрать конверт и марку для отправки письма?
11. Из трех экземпляров учебника алгебры, семи экземпляров учебника геометрии и шести экземпляров учебника физики надо выбрать комплект, содержащий все три учебника по одному разу. Сколькими способами это можно сделать?
12. В корзине лежит 12 яблок и 10 апельсинов. Ваня выбирает либо яблоко, либо апельсин, после чего Надя выбирает из оставшихся фруктов и яблоко, и апельсин. Сколько возможно таких выборов? При каком выборе Вани у Нади больше возможностей выбора?
Занятие 3. Размещения
Цели занятия:
• проверить усвоение правила произведения;
• сформулировать определение размещений с повторениями и без повторений;
• закрепить на задачах число размещений с повторениями или без повторений.
Проверка домашней работы
Первые две задачи подобны тем, которые разбирались в классе. Рассмотрим решение задачи 3.
На шахматной доске 64 клетки: 32 белых квадрата, 32 черных квадрата. Поэтому по правилу произведения находим число способов выбора двух квадратов: одного белого и одного черного: 32 • 32 = 1024.
Если нет ограничений на цвет, то первый квадрат можно выбрать 64 способами, а второй квадрат — 63 способами (один квадрат уже выбран). Поэтому общее число способов равняется 64 • 63 = 4032.
Если надо выбрать два белых квадрата, то первый квадрат можно выбрать 32 способами, а второй квадрат — 31 способом. Поэтому общее число способов равно 32 • 31 = 992.
Размещения с повторениями
ОПРЕДЕЛЕНИЕ. Множества Х1,…. Xk, из элементов которых составляются кортежи, могут иметь общие элементы. В частности, все они могут совпадать с одним и тем же множеством X, состоящим из п элементов. Кортежи длины k, составленные из элементов п-множества X, называют размещениями с повторениями из п элементов по k, а их число обозначают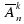 
.
Из правила произведения сразу вытекает, что число размещений с повторениями из п элементов по k равно произведению k сомножителей, каждый из которых равен п:
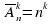
Перед решением задач с учащимися необходимо по данной формуле вычислить несколько значений, чтобы при решении задач не возникало трудностей работы с самой формулой.
Упражнение. Вычислите: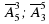 
Решение.
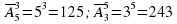
Задача 1. Для запирания автоматической камеры применяется секретный замок, который открывается лишь тогда, когда набрано «тайное слово». Это слово набирают с помощью пяти дисков, на каждом из которых изображено 12 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова и подбирающего его наудачу?
Решение. Из условия задачи видно, что порядок выбираемых букв существенен. Поэтому мы имеем дело с кортежем длиной 5 (пять дисков). Каждый элемент кортежа может быть выбран 12-ю способами (букв на каждом диске 12). Поэтому число комбинаций равно 125 = 248832. Следовательно, неудачных попыток может быть 248831.
Ответ: 248 831.
Задача 2. Сколько различных четырехзначных чисел можно составить из цифр 2, 6, 7, 8 и 9, если каждая цифра может входить в комбинацию несколько раз?
Решение. Здесь порядок цифр существенен (2678 или 6278 — это разные числа). Поэтому имеем дело с кортежем длины 4 (четырехзначное число), каждый элемент которого можно выбрать пятью способами (цифр дано пять). Поэтому число различных комбинаций равно 45 = 1024.
Ответ: 1024.
Задача 3. На референдуме предложены четыре вопроса, на которые надо ответить «да» или «нет». Сколько есть возможностей заполнения бюллетеня (на все вопросы надо дать ответ)?
Решение. Получаем кортеж длины 4 (столько вопросов в бюллетене), каждый элемент может быть выбран двумя способами («да» или «нет»). Поэтому число различных возможностей равно 24 = 16.
Ответ: 16.
Задача 4. Неудовлетворенные решением Париса Гера, Афина и Афродита обратились к трем мудрецам с просьбой назвать прекраснейшую из них. Каждый из мудрецов высказал свое мнение. Сколько могло возникнуть вариантов ответа на поставленный вопрос у этой тройки?
Решение. Здесь вновь кортеж длиной 3 (три мудреца), каждый элемент которого может быть выбран шестью способами. Поэтому число различных возможностей равно 63 = 216.
Ответ: 216.
Задача 5. У Лены есть восемь красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если собирается каждую букву раскрашивать одним цветом?
Решение. Кортеж длиной 8 (восемь букв), каждый элемент может быть выбран восемью способами (восемь красок). Поэтому число способов равно 88.
Ответ: 88.
Задачи для домашней работы
1. Сколько букв русского алфавита можно закодировать, используя лишь комбинации точек и тире, содержащие только три знака?
2. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать?
Ответы: 1. 8. 2. 1728.
Размещения без повторений
ОПРЕДЕЛЕНИЕ. Произведение всех чисел от 1 до n называется факториалом и обозначается n!. В комбинаторике 0! = 1 и 1! = 1.
Упражнение. Вычислите: 4!; 6!.
Решение. 4! = 4 • 3 • 2 • 1 = 24;
6! = 6∙5∙4∙3∙2∙1 = 720.
При решении комбинаторных задач часто необходимо вычислить факториал, поэтому целесообразно вывешивать на доску следующую таблицу.
| п | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| n! | 2 | 6 | 24 | 120 | 720 | 5040 | 40 320 | 362 880 | 3 628 800 | 39 916 800 |
ОПРЕДЕЛЕНИЕ. Кортежи длины k, составленные из элементов n-множества X так, что все элементы каждого кортежа должны быть различными, называют размещениями без повторений из п элементов по k,а их число обозначают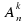 
.
Чтобы сосчитать 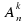, будем рассуждать так: на первое место п кандидатов. После того, как оно заполнено, на второе место остается п - 1 кандидат, на третье место — п - 2 кандидата и т.д. На k-e место имеется п - k + 1 кандидат. Применяя правило произведения, находим
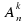= п(п - 1)∙ ... ∙(п - k + 1).
Эту формулу можно записать иначе, умножив числитель и знаменатель на (п - k) •... • 1:
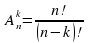
Упражнение. Вычислите: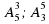
Решение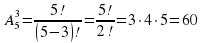 
Из определения размещений без повторений следует, что п k, поэтому вычислить нельзя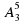 
.
Задача 1. В высшей лиге первенства по футболу участвуют 16 команд. Разыгрывается три медали: золотая, серебряная и бронзовая. Перед началом первенства был объявлен конкурс знатоков, в котором требовалось указать распределение медалей. Сколько различных ответов можно дать на этот вопрос?
Решение. Здесь речь идет о кортежах длины 3. Но ни один элемент не может входить дважды (одна и та же команда не может получить и золотую, и серебряную медали). Значит, число различных ответов находим следующим образом:
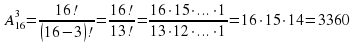
Ответ: 3360.
Задача 2. Из спортивного клуба, насчитывающего 30 членов, надо составить команду из четырех человек для участия в эстафете на 100 + 200 + 400 + 800 (м). Сколькими способами это можно сделать?
Решение. Имеем кортежи длиной 4. Ни один элемент не может входить дважды (один бегун на один отрезок дистанции). Значит,
.
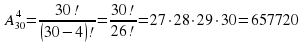
Ответ: 657 720.
Задача 3. Сколькими способами можно обозначить вершины данного треугольника, используя буквы А, В, С, D, Е и F?
Решение. Имеем кортежи длиной 3 (у треугольника три вершины). Ни один элемент не может входить дважды. Значит,
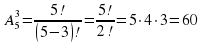
Ответ: 60.
Задачи для домашней работы
1. Сколько всего различных пятизначных чисел, не содержащих нуля?
2. В классе изучают девять предметов. Сколькими способами можно составить расписание на понедельник, если в этот день должно быть шесть разных уроков?
Ответы: 1. 15 120. 2. 720.
Дополнительные задачи
Размещения с повторениями
1. Сколькими способами можно разделить шесть различных конфет между тремя детьми?
2. Сколько существует пятизначных номеров, не содержащих цифру 8?
3. Сколькими способами можно разложить 12 различных деталей по трем ящикам?
4. Имеется набор из 16 карточек. На четырех из них написана буква «А», на четырех — буква «Б», на четырех — буква «В» и на четырех — буква «Г». Сколько различных комбинаций букв можно получить, выбирая из набора четыре карточки и располагая их в некотором порядке?
5. В некотором сказочном королевстве не было двух человек с одинаковым набором зубов. Каково может быть наибольшее число жителей этого королевства, если у человека 32 зуба?
Размещения без повторений
1. В классе 30 человек. Сколькими способами могут быть выбраны из них староста и казначей?
2. В чемпионате по футболу участвуют десять команд. Сколько существует различных возможностей занять командам первые три места?
3. В цехе работают восемь токарей. Сколькими способами можно поручить трем из них изготовление трех различных видов деталей (по одному виду на каждого)?
4. Из десяти различных книг выбирают четыре для посылки. Сколькими способами это можно сделать?
5. В профком избраны семь человек. Из них надо выбрать председателя, его заместителя и секретаря. Сколькими способами это можно сделать?
6. Сколькими способами можно опустить пять писем в 11 почтовых ящиков; если в каждый ящик опускают не более одного письма?
7. Сколькими различными способами можно распределить между шестью лицами две различные путевки в санаторий?
8. В турнире по шахматам каждый участник сыграл с каждым по одной партии, всего было сыграно 36 партий. Определите число участников турнира.
Занятие 4. Перестановки
Цели занятия:
• проверить усвоение темы прошлого занятия через проверку домашнего задания;
• познакомить учащихся с перестановками без повторений и с повторениями;
• закрепить новую тему при решении задач.
В начале урока проверить решение задач, заданных на дом.
Решить следующую задачу.
Задача. На железнодорожной станции имеется п семафоров. Сколько может быть дано различных сигналов при помощи этих семафоров, если каждый семафор имеет три состояния: горит либо зеленый, либо желтый, либо красный свет.
Решение. Имеем кортеж длины п (дано п семафоров), каждый элемент которого можно выбрать тремя способами (каждый семафор имеет три состояния). Поэтому различных сигналов можно дать 3n.
Ответ: 3n.
Перестановка без повторений
ОПРЕДЕЛЕНИЕ. Два размещения без повторений из п элементов по п состоят из одних и тех же элементов, расположенных в различном порядке. Такие размещения называют перестановками из п элементов. Их число обозначают Рп:
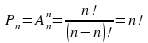
Упражнение. Вычислите: Р3; Р5.
Решение. Р3 = 3! = 6;
Р5 = 5! = 120.
Задача 1. Найдите число способов расстановки восьми ладей на шахматной доске, при которых они не бьют друг друга.
Решение. Каждый искомый способ задается перестановкой восьми чисел 1, 2, …,8. Эти числа указывают номера горизонталей занятых полей на первой, второй,…, восьмой вертикалях. Значит, таких перестановок 8!. Таким образом, ладьи можно расставить 8! = 40 320 способами.
Ответ 40320
Задача 2. Сколькими способами можно переставлять друг с другом цифры 1, 2, 3 и 4?
Решение. Р4 = 4! = 24.
Ответ: 24.
Задача 3. За столом пять мест. Сколькими способами можно рассадить пятерых гостей?
Решение. Р5 = 5! = 120.
Ответ: 120.
Задача 4. У Лены есть восемь разных красок. Она хочет написать ими слова «Новый Год». Сколькими способами она может это сделать, если каждая буква должна быть раскрашена одним цветом и все восемь букв должны быть разными по цвету?
Решение. Присвоим каждой краске номер от 1 до 8. Тогда каждый искомый способ задается перестановкой восьми чисел 1, 2,…, 8. Значит, таких перестановок 8!. Поэтому она может написать «Новый Год» 8! = 40 320 способами.
Ответ: 40 320.
Перестановки с повторениями
ОПРЕДЕЛЕНИЕ. Пусть дан кортеж длины п, составленный из элементов множества X = {х1,…, xk}. Причем буква х1 входит в этот кортеж n1, раз,…, буква xk — пk раз. Тогда п = n1 + ... + nk.. Если переставлять в этом кортеже буквы, то будут получаться новые кортежи, имеющие тот же состав. Эти кортежи называются перестановками с повторениями из букв x1,…xk, имеющими состав (n1, .., nk). Число таких перестановок обозначим Р(n1, .., nk).
Р(n1, .., nk)=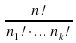
где п = n1+ …+ nk.
Упражнение. Вычислите: Р{2, 5, 3);
Решение. Р(2, 5, 3); п = 2 + 5 + 3 = 10, п1 = 2, n2 = 5, n3 = 3.
Р(2, 5, 3) =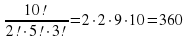 
Задача 1. Сколько различных кортежей получится, если переставлять буквы слова «математика»?
Решение. Это слово имеет состав: м — 2, а — 3, т — 2, е — 1, и — 1, к — 1, то есть (2, 3, 2, 1, 1, 1), поэтому получим
Р(2, 3, 2, 1, 1, 1) =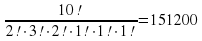 
Ответ: 151 200.
Задача 2. У мамы два яблока и три груши. Каждый день в течение пяти дней она дает сыну по одному фрукту. Сколькими способами это может быть сделано?
Решение. Р(2, 3) =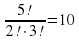 
Ответ: 10.
Задача 3. Сколькими способами можно положить 28 различных открыток в четыре одинаковых конверта так, чтобы в каждом конверте было по семь открыток?
Решение. Пометим конверты цифрами 1, 2, 3 и 4. Тогда число различных раскладок равно
Р(7, 7, 7, 7) =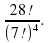 
Сотрем пометки. Теперь конверты можно произвольно переставлять друг с другом, не меняя результата раскладки (теперь они неотличимы друг от друга). Так как число различных перестановок четырех конвертов равно Р4 = 4!, то число различных раскладок уменьшается в Р4 = 4! раз и поэтому оно равно.
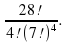
Ответ: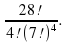
Задачи для домашней работы
1. Сколько различных слов можно получить, переставляя буквы слова «ингредиент»?
2. Сколькими способами можно посадить за круглый стол пять мужчин и пять женщин так, чтобы никакие два лица одного пола не сидели рядом?
3. Автомобильные номера состоят из четырех цифр и трех букв. Найдите число таких номеров, если используются 32 буквы русского алфавита.
Ответы: 1. 226 800. 2. 5! • 5! = 14 400. 3. 103 • 323.
Дополнительные задачи
Перестановки с повторениями
1. Сколькими различными способами можно усадить за стол трех мальчиков и трех девочек так, чтобы никакие две девочки не сидели рядом?
2. Задача-шутка. Как-то раз в воскресенье семеро друзей зашли в кафе. Хозяин кафе сказал, что если друзья в каждое следующее воскресенье будут садиться по-разному и перепробуют все способы посадки, то с этого момента он обещает кормить всех мороженым бесплатно. Удастся ли друзьям воспользоваться предложением хозяина кафе?
3. Сколькими способами можно разложить 28 различных предметов по четырем различным ящикам так, чтобы в каждом ящике, оказалось по семь предметов?
4. Для премирования победителей математической олимпиады выделено три экземпляра одной книги, четыре экземпляра другой и восемь экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
5. Сколькими способами можно переставлять буквы слова «огород», чтобы три буквы «о» не шли подряд?
Перестановки без, повторений
1. Сколькими способами можно разместить 12 человек за столом, на который поставлено 12 приборов?
2. Сколькими способами можно установить дежурство по одному человеку в день среди семи учащихся группы в течение семи дней?
3. Сколько пятизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1, 2, 3, 4 и 5 так, чтобы:
а) последней была цифра 4;
б) первой была цифра 2, а второй 3?
4. Имеется 10 книг, среди которых:
а) восемь книг разных авторов и двухтомник одного автора, которого не было среди предыдущих семи;
б) семь книг разных авторов и трехтомник восьмого автора.
Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора не стояли рядом?
Занятие 5. Сочетания
Цели занятия:
• дать понятие сочетаний с повторениями и без повторений;
• закрепить тему при решении задач.
В начале урока разбираются задачи, заданные на дом.
Сочетания с повторениями
ОПРЕДЕЛЕНИЕ 1. Два кортежа называются эквивалентными, если они имеют одинаковый состав.
ОПРЕДЕЛЕНИЕ 2. Классы эквивалентности, на которые разбивается вся совокупность кортежей длины k из п элементов, называются сочетаниями с повторениями п элементов по k, их число обозначают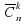 
.
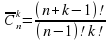
Упражнение. Вычислите: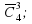 
Решение.
Задача 1. В кондитерском отделе продаются пирожные четырех сортов: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить семь пирожных?
Решение. Здесь рассматриваются сочетания с повторениями из 4 (четыре вида пирожных) по 7 (столько пирожных покупают). Значит,
Ответ: 120 способов.
Задача 2. В почтовом отделении продают открытки 10 видов. Сколькими способами можно купить в нем 12 открыток?
Решение. Здесь рассматриваются сочетания с повторениями из 10 по 12. Имеем
Ответ: 293 930.
Сочетания без повторений
ОПРЕЛЕЛЕНИЕ. Число k-подмножеств в п-множестве X называют сочетаниями из п по k. Число таких сочетаний обозначают 
.
Упражнение. Вычислите: 
.
Решение.
По определению сочетаний без повторений следует, что k . Поэтому вычислить 
нельзя.
Задача 1. Сколькими способами в игре «Спортлото» можно выбрать шесть номеров из 49?
Решение. Здесь рассматриваются сочетания без повторения (одно число может быть по правилам игры выбрано не более одного раза) из 49 по 6.
Ответ: 13 983 816.
Задача 2. У Робина-Бобина Барабека 40 соседей. Он решил пригласить двоих из них на обед. Сколько у него способов это сделать?
Решение. Здесь рассматриваются сочетания без повторений.
Ответ: 780.
Задача 3. Дама сдавала в багаж семь предметов. Все они оказались украденными, но два каких-либо (по ее выбору) ей согласились поискать. Сколько у нее есть возможностей выбрать два любимых предмета?
Решение.
Ответ: 21.
Задача 4. В прошлые века процветала генуэзская лотерея, сохранившаяся в некоторых странах и поныне. Участники этой лотереи покупали билеты, на которых стояло число от 1 до 90. Можно было купить и билеты, на которых было сразу 2, 3, 4 и 5 чисел. В день розыгрыша лотереи из мешка, содержащего жетоны с числами от 1 до 90, вынимали пять жетонов. Выигрывали те, у которых все номера на билетах были среди вынутых. Если участник лотереи покупал билет с одним числом, то он получал при выигрыше в 15 раз больше стоимости билета; если с двумя числами (амбо), то в 270 раз больше, если с тремя числами (терн) — в 5500 раз больше, если в четырьмя числами (катерн) — в 75 000 раз больше, а если с пятью числами (квин) — в 1 000 000 раз больше, чем стоил билет. Каково отношение «счастливых» билетов при игре, когда участник купил билет с одним числом?
Решение. Общее число исходов находится из формулы сочетаний без повторений:
Если участник купил билет с одним номером, то для выигрыша необходимо, чтобы один из вынутых номеров совпал с номером на билете. Остальные 4 номера могут быть благоприятными. Но эти 4 номера выбираются из оставшихся 89 номеров. Поэтому число благоприятных комбинаций выражается формулой
Отсюда следует, что отношение числа благоприятных комбинаций к общему числу комбинаций равно
Ответ: 
.
Задачи для домашней работы
1. Сосчитайте, каково отношение «счастливых» билетов при игре, когда участник купил билет с двумя числами.
2. Сколькими способами можно составить набор из восьми пирожных, если имеется четыре сорта пирожных?
3. В классе имеется шесть сильных математиков. Сколькими способами из них можно составить команду на районную олимпиаду по математике, если от класса можно послать команду из четырех человек?
Ответы: 1. 
2. 165. 3. 15.
Дополнительные задачи
Сочетания с повторениями
1. Сколько существует треугольников, длины сторон которых принимают одно из следующих значений: 4 см, 5 см, 6 см и 7 см?
2. Сколько можно построить различных прямоугольных параллелепипедов, длины ребер которых выражаются натуральными числами от 1 до 10?
Сочетания без повторений
1. Сколькими способами можно составить команду из четырех человек для соревнований по бегу, если имеется семь бегунов?
2. Сколькими способами можно выбрать пять делегатов из участников конференции, на которой присутствуют 15 человек?
3. Сколькими способами можно поставить восемь шашек на черные поля доски?
4. Сколькими способами можно поставить на черные поля 12 белых и 12 черных шашек?
5. У одного человека есть 11 книг по математике, у другого 15 книг. Сколькими способами они могут выбрать по три книги для обмена?
6. Сколькими способами можно распределить две одинаковые путевки между пятью лицами?
7. Сколькими способами можно присудить шести лицам три одинаковые премии?
8. В классе 30 учащихся. Сколькими способами можно:
а) назначать двух дежурных;
б) выбрать 28 человек для осеннего кросса.
Занятие 6. Решение задач
Цели занятия:
• закрепить навыки решения комбинаторных задач простейшего типа.
Задача 1. На плоскости проведено п прямых, причем никакие две из них не параллельны и никакие три из них не пересекаются в одной точке. Сколько точек пересечения имеют эти прямые?
Решение. Каждая точка пересечения однозначно определяется парой проходящих через нее прямых. При этом порядок прямых роли не играет. Поэтому искомое число точек пересечения равно числу сочетаний из п по 2, то есть
Ответ: 
Задача 2. В местком избрано девять человек. Из них надо выбрать председателя, заместителя председателя и культорга. Сколькими способами это можно сделать?
Решение. Здесь идет речь о размещениях без повторений. Имеем
Рассуждать можно было по-другому. Нужно найти число кортежей длины 3 (на три должности выбирают). На первую должность выбираем из девяти человек, на вторую — из восьми человек, на третью — из семи человек. По правилу произведения получаем 9∙8∙7 = 504.
Ответ: 504.
Задача 3. Из точек и тире составляют всевозможные кортежи длиной 7. Какое число различных кортежей можно составить?
Решение. Здесь имеем дело с размещениями с повторениями из двух элементов (тире и точки) по 7 (длина кортежа). Поэтому искомое число находится следующим образом:
Ответ: 128.
Задача 4. Сколько различных браслетов можно сделать из пяти одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Получаем перестановки с повторениями. Их число будет равно
Ответ: 
Задача 5. Из 12 слов мужского рода, 9 слов женского и 10 среднего нужно выбрать по одному слову каждого рода. Сколькими способами может быть сделан выбор?
Решение. По правилу произведения находим, что искомое число равно 12 ∙ 9∙ 10 = 1080.
Ответ: 1080.
Задача 6. У профессора есть три любимых каверзных вопроса. В группе 20 студентов.
а) Профессор решил задавать каждому из студентов по одному из каверзных вопросов. Сколько есть возможностей провести опрос в группе?
б) Профессор решил наудачу по списку группы выбрать студента, чтобы задать ему первый вопрос, потом опять из всего списка выбрать второго студента, чтобы задать ему второй вопрос, потом так же выбрать третьего студента. Сколько у него возможностей провести опрос в этом случае?
в) Профессор решил спрашивать только троих студентов, каждому по одному вопросу (так, чтобы вопросы не повторялись). Сколько у него есть возможностей в этом случае?
Решение а) Здесь, кортеж длиной 20 (20 студентов), каждый элемент которого можно выбрать тремя способами (три вопроса). Значит, речь идет о размещениях с повторениями.
б) Кортеж длиной 3 (три вопроса), первый элемент можно выбрать 20-ю способами (20 студентов), второй элемент — 19-ю способами (осталось 19 неопрошенных студентов), третий — 18-ю способами. По правилу произведения определяем число возможностей: 20 ∙ 19 ∙ 18 = 6840.
Можно рассуждать по-другому. Речь идет о кортежах длиной 3 (три вопроса). Ни один элемент не может входить дважды. Следовательно, речь идет о размещениях без повторений.
в) Здесь профессор из 20 студентов выбирает троих. Следовательно, имеем сочетание без повторений.
Ответ: а) З20; б) 6840; в) 1140.
Задачи для домашней работы
1. Имеется пять видов конвертов без марок и четыре вида с марками. Сколькими способами можно выбрать конверт с маркой для посылки письма?
2. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти различных цветов?
3. Сколькими способами можно составить четырехцветный флаг из горизонтальных полос, имея четыре различных цвета?
4. Из колоды, содержащей 52 карты, вынули десять карт. Сколькими различными способами это можно сделать?
Ответ: 1. 5 • 4 = 20. 2. 
= 60. 3. Р4 = 4! = 24. 4
Занятие 7. Решение задач
Цель занятия: закрепление навыков решения простейших комбинаторных задач.
Задача 1. Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной горизонтали или вертикали?
Решение. Белый квадрат можно выбрать 32 способами (произвольными). Черный квадрат — 24 способами (из 32 вычитаем 8, лежащих на одной горизонтали или вертикали с выбранным белым). По правилу произведения получаем искомое число 768.
Ответ: 768.
Задача 2. У одного человека есть семь книг по математике, у другого — девять книг. Сколькими способами они могут обменять три книги одного на три книги другого?
Решение. Найдем, сколько троек из семи книг можно составить у первого человека:
Число троек из девяти книг у второго человека равно
По правилу произведения находим число обменов: 35∙84 = 2940.
Ответ: 2940.
Задача 3. Сколькими способами можно расставить белые фигуры (два короля, два слона, две ладьи, ферзь и король) на первой линии шахматной доски?
Решение. Надо найти число кортежей длины 8, имеющих состав (2, 2, 2, 1, 1). Число таких перестановок с повторениями равно
Ответ: 5040.
Задача 4. 15 пронумерованных биллиардных шаров разложены по шести лузам. Сколькими способами это можно сделать?
Решение. Имеем размещения с повторениями из 6 элементов (в шесть луз) по 15 (15 шаров). Их число
равно
Ответ: 
Задача 5. Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?
Решение. Имеем кортежи длиной 3 (а, b, с). Элемент а может быть выбран 3 способами (три офицера) элемент b (два сержанта из шести) можно выбрать 
способами, элемент с (20 солдат из 60) —
способами. По правилу произведения находим число выбора исходных кортежей:
3∙30∙ =90∙.
Ответ: 90∙.
Получите свидетельство
Вход
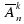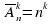
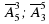
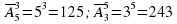
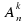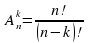
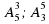
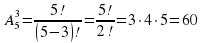
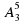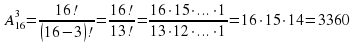
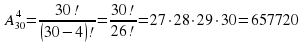
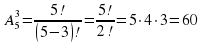
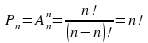
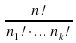
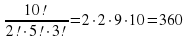
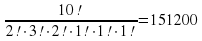
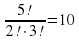
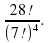
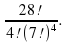
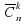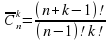
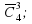
Прикладной курс по математике "Комбинаторика" (69.97 КB)
0
2749
193
Нравится
0
