Получите свидетельство
Вход
Урок №3
Учитель Садовская Н.П.
11.09.17
Цели:
актуализировать и сформулировать определения монотонности и ограниченности функции на множестве; формировать умение определять данные свойства по графику и аналитической записи функции.
11.09.17
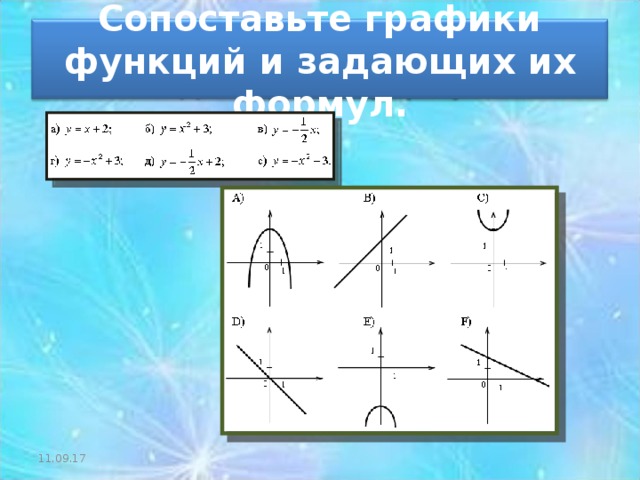
Сопоставьте графики функций и задающих их формул.
11.09.17
Найдите область определения функции, заданной формулой.
11.09.17
Свойства функции
11.09.17
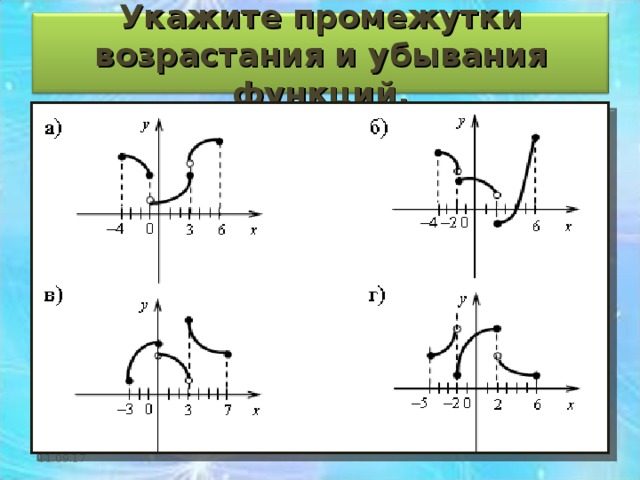
Укажите промежутки возрастания и убывания функций.
11.09.17
f (х 2 ). f(x 2 ) f(x 1 ) f(x 1 ) f(x 2 ) x 2 х 1 x 1 x 2 " width="640"
СВОЙСТВА ФУНКЦИИ
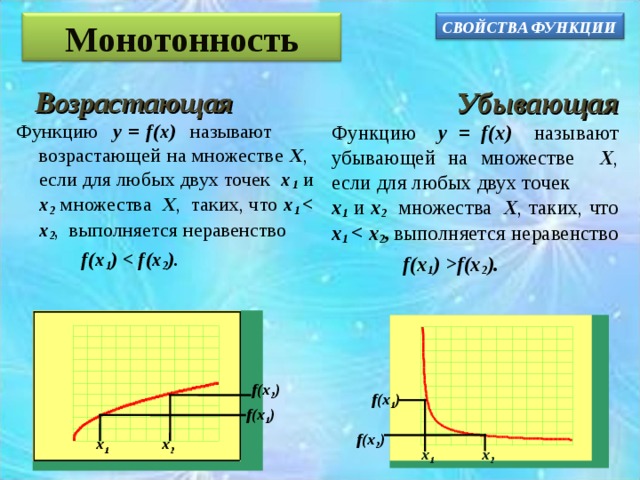
Монотонность
Возрастающая
Функцию у = f (х) называют возрастающей на множестве Х , если для любых двух точек х 1 и х 2 множества Х , таких, что х 1 х 2 , выполняется неравенство
f (х 1 ) (х 2 ).
Убывающая
Функцию у = f (х) называют убывающей на множестве Х , если для любых двух точек
х 1 и х 2 множества Х , таких, что х 1 х 2 , выполняется неравенство
f (х 1 ) f (х 2 ).
f(x 2 )
f(x 1 )
f(x 1 )
f(x 2 )
x 2
х 1
x 1
x 2
СВОЙСТВА ФУНКЦИИ
Наибольшее и наименьшее значения
Число m называют наименьшим значением функции
у = f (х) на множестве Х , если:
- в Х существует такая точка х 0 , что f (х 0 ) = m .
- для всех х из Х выполняется неравенство
f (х) ≥ f (х 0 ).
Число M называют наибольшим значением функции
у = f (х) на множестве Х , если:
1) в Х существует такая точка х 0 , что f (х 0 ) = M .
2) для всех х из Х выполняется неравенство
f (х) ≤ f (х 0 ).
СВОЙСТВА ФУНКЦИИ
Непрерывность
Непрерывность функции на промежутке Х означает, что график функции на промежутке Х сплошной, т.е. не имеет проколов и скачков.
Задание: Определите, на каком из рисунков изображен график непрерывной функции.
Ты не прав…
Молодец!!!
1
2
СВОЙСТВА ФУНКЦИИ
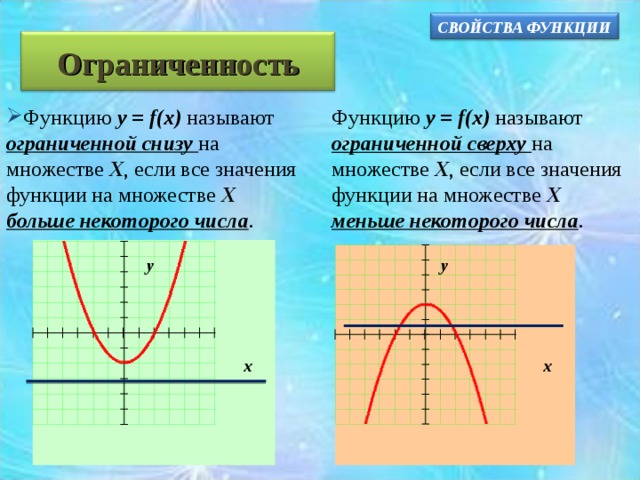
Ограниченность
- Функцию у = f (х) называют ограниченной снизу на множестве Х , если все значения функции на множестве Х больше некоторого числа .
Функцию у = f (х) называют ограниченной сверху на множестве Х , если все значения функции на множестве Х меньше некоторого числа .
у
у
х
х
Выполните задания
- Нарисуйте схематично график функции, возрастающей на промежутках (– ∞ ; –2) и (5; + ∞ ) и убывающей на промежутке (–2; 5).
- Пример 1 со с. 11 учебника исследование функции на монотонность с использованием неравенств.
- Схематично изобразить графики элементарных функций и выбрать среди них ограниченные.
- Пример 2 со с. 12 учебника исследования функции на ограниченность с помощью неравенств.
11.09.17
Формирование умений и навыков.
1-я группа. Исследование функции на монотонность с использованием свойств числовых неравенств.
2-я группа. Исследование функции на ограниченность с использованием свойств числовых неравенств.
№ 2.1 (а; б), № 2.2 (а; б), № 2.3 (а; б), № 2.4 (а; б), № 2.5 (а; б).
11.09.17
Итоги урока.
11.09.17
Домашнее задание:
№ 2.1 (в; г) – № 2.7 (в; г).
11.09.17
Презентация урока алгебры 10 класса по теме "Свойства функции" (2.1 MB)
0
4033
713
Нравится
0
