
Степенные функции .
Их свойства и графики.
Л.С. Атанасян. Геометрия 10-11.
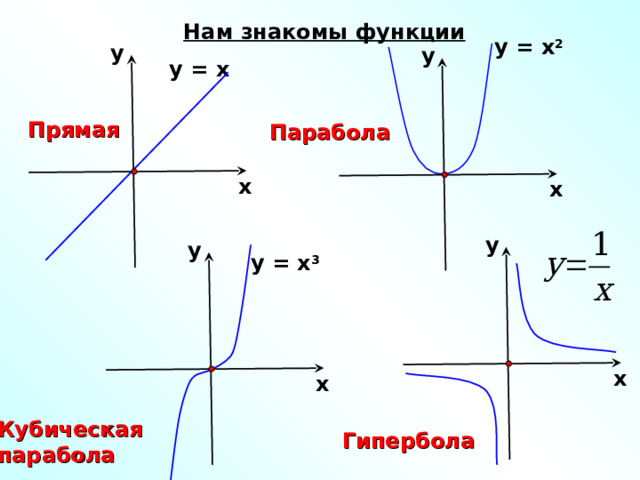
Нам знакомы функции
- Нам знакомы функции
- Нам знакомы функции
- Нам знакомы функции
- Нам знакомы функции
у = х 2
у
у
у = х
Прямая
Парабола
х
х
у
у
у = х 3
х
х
Кубическая
парабола
Гипербола
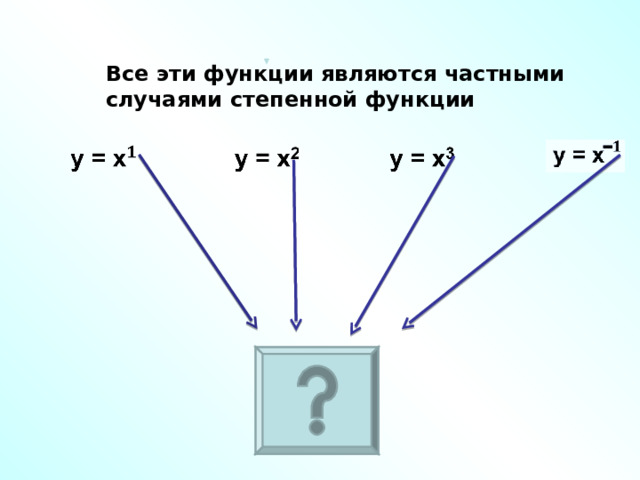
Все эти функции являются частными случаями степенной функции
- Все эти функции являются частными случаями степенной функции
- Все эти функции являются частными случаями степенной функции
- Все эти функции являются частными случаями степенной функции
- Все эти функции являются частными случаями степенной функции
2

Степенными функциями
называют функции вида
у = х р
(р – заданное действительное число).
Свойства и график степенной функции
зависят от показателя степени
- Свойства и график степенной функции зависят от показателя степени
- Свойства и график степенной функции зависят от показателя степени
- Свойства и график степенной функции зависят от показателя степени
- Свойства и график степенной функции зависят от показателя степени
Опорный конспект
- Опорный конспект
- Опорный конспект
- Опорный конспект
- Опорный конспект
2
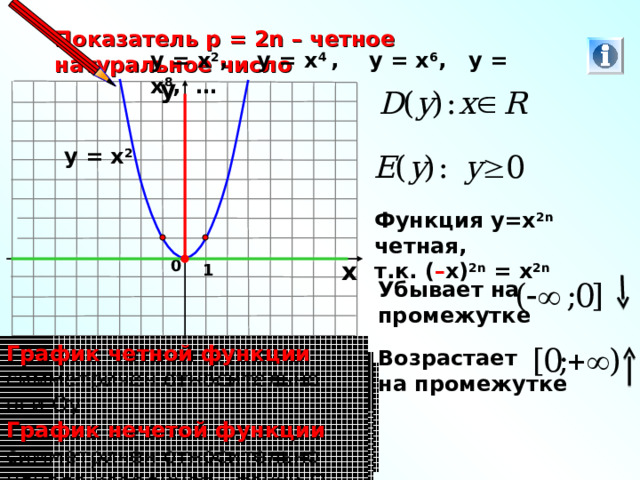
Показатель р = 2n – четное натуральное число
у = х 2 , у = х 4 , у = х 6 , у = х 8 , …
у
у = х 2
Функция у=х 2 n четная,
т.к. ( – х) 2 n = х 2 n
0
х
1
Убывает на промежутке
График четной функции симметричен относительно оси Оу.
График нечетой функции симметричен относительно начала координат – точки О.
Возрастает
на промежутке
Область значений функции –
множество значений,
которые может принимать
переменная у
Область определения функции –
значения, которые может принимать переменная х
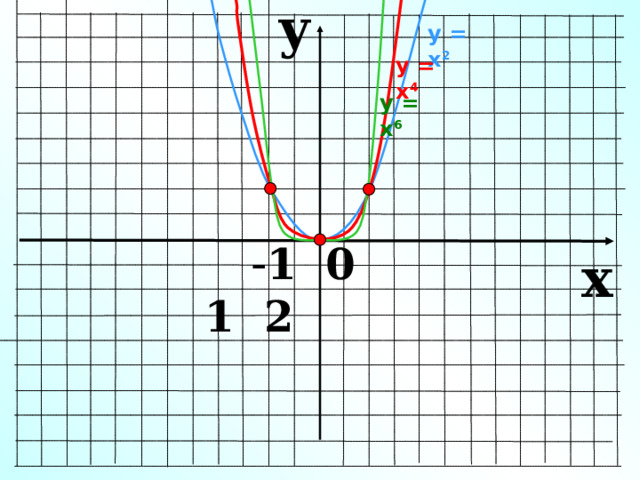
y
у = х 2
у = х 4
у = х 6
- 1 0 1 2
x
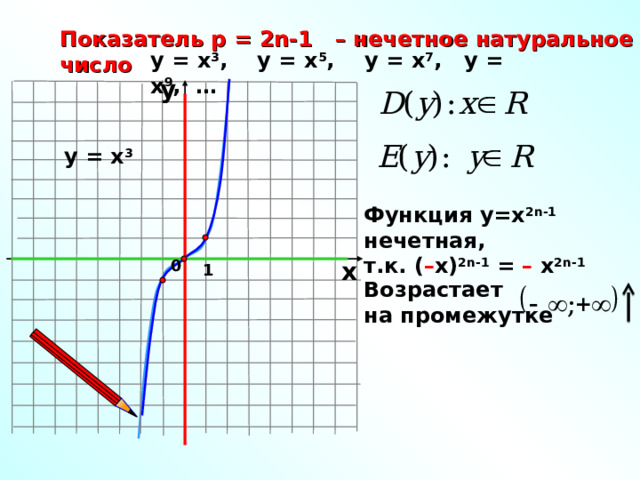
Показатель р = 2n -1 – нечетное натуральное число
у = х 3 , у = х 5 , у = х 7 , у = х 9 , …
у
у = х 3
Функция у=х 2 n -1 нечетная,
т.к. ( – х) 2 n -1 = – х 2 n -1
0
х
1
Возрастает
на промежутке
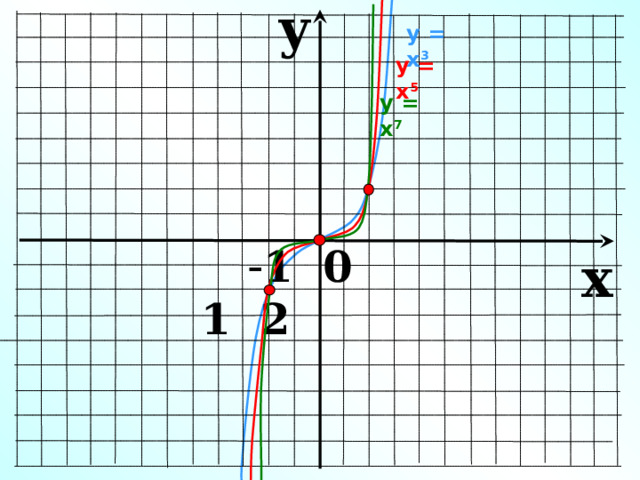
y
у = х 3
у = х 5
у = х 7
- 1 0 1 2
x
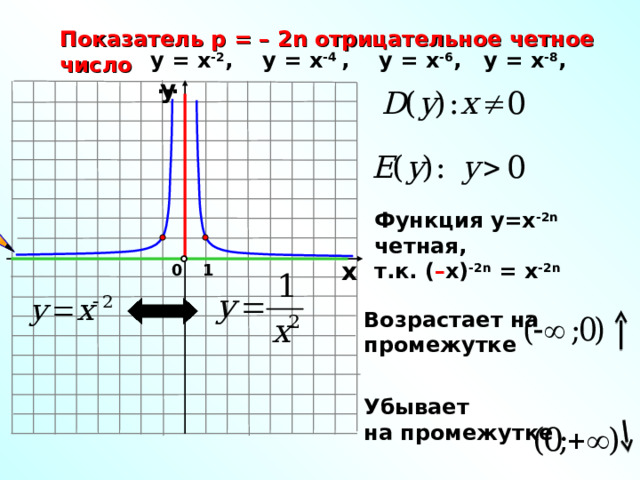
Показатель р = – 2n отрицательное четное число
у = х -2 , у = х -4 , у = х -6 , у = х -8 , …
у
Функция у=х -2 n четная,
т.к. ( – х) -2 n = х -2 n
х
0
1
Возрастает на
промежутке
Убывает
на промежутке
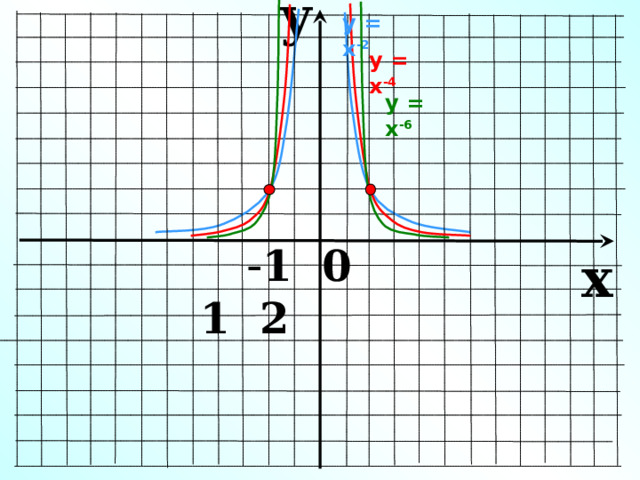
y
у = х -2
у = х -4
у = х -6
- 1 0 1 2
x
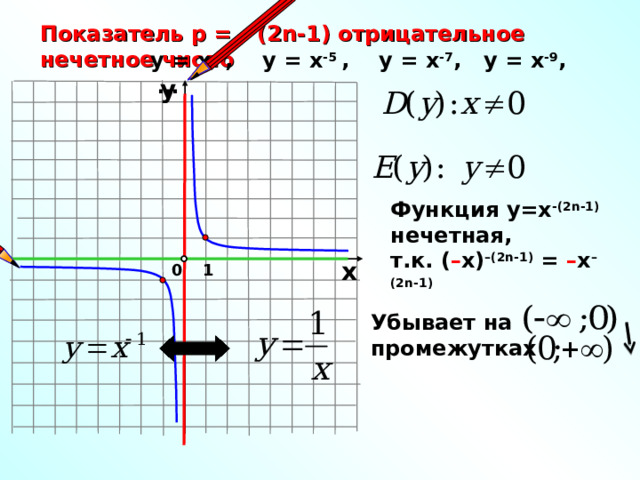
Показатель р = – ( 2n -1) отрицательное нечетное число
у = х -3 , у = х -5 , у = х -7 , у = х -9 , …
у
Функция у=х -(2 n -1) нечетная,
т.к. ( – х) –(2 n -1) = – х –(2 n -1)
х
1
0
Убывает на
промежутках
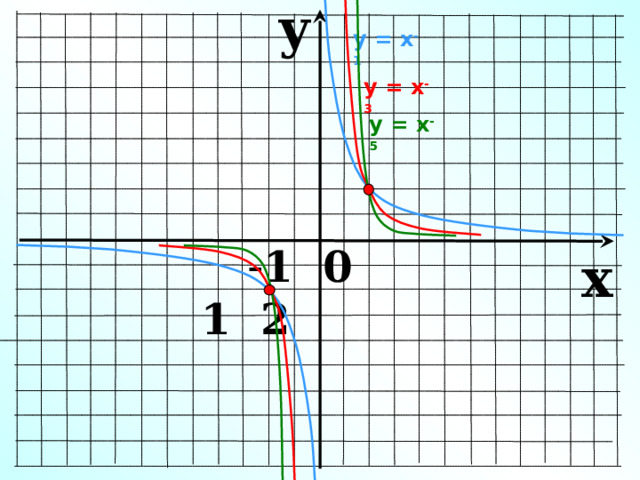
y
у = х -1
у = х -3
у = х -5
- 1 0 1 2
x
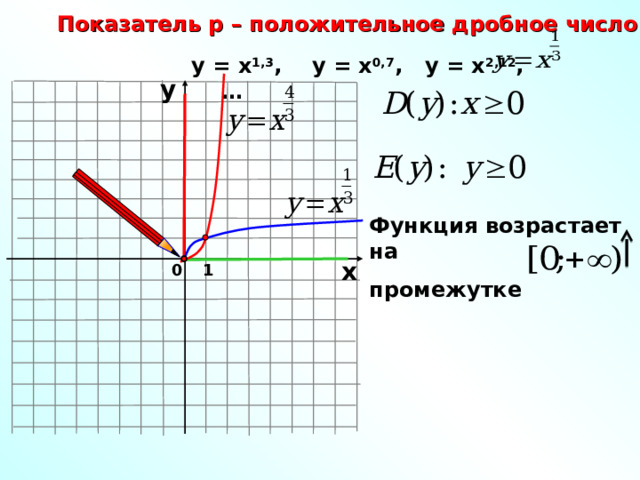
Показатель р – положительное дробное число
у = х 1,3 , у = х 0,7 , у = х 2,12 , …
у
Функция возрастает на
промежутке
х
0
1
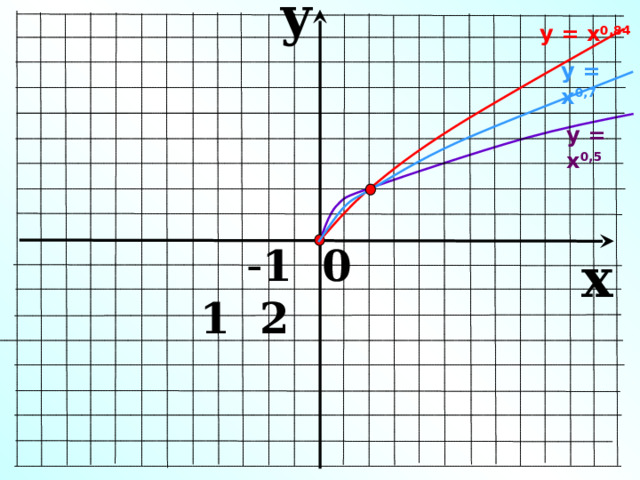
y
у = х 0,84
у = х 0,7
у = х 0,5
- 1 0 1 2
x
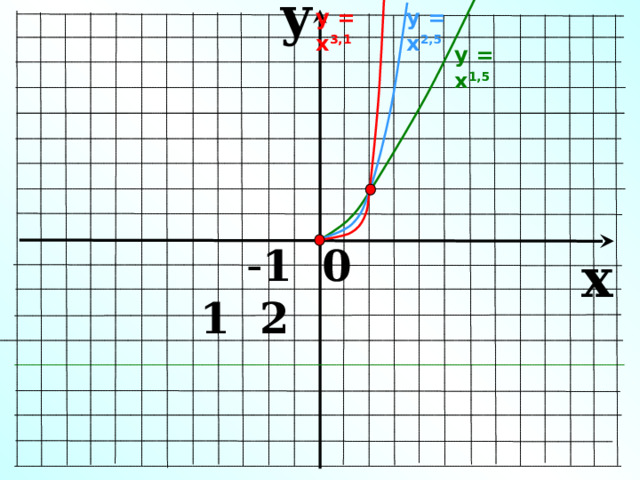
y
у = х 2,5
у = х 3,1
у = х 1,5
- 1 0 1 2
x
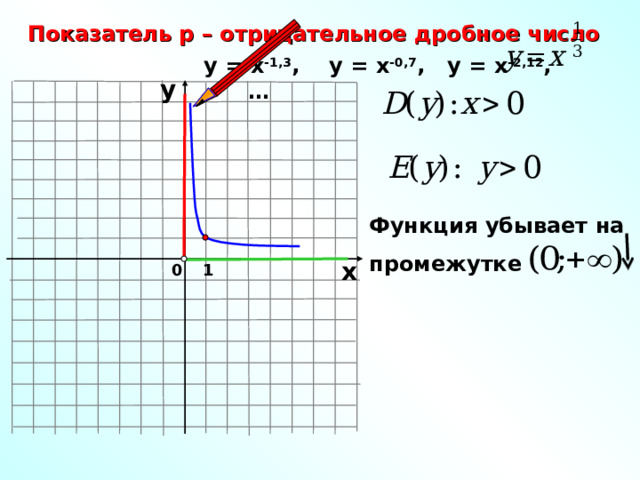
Показатель р – отрицательное дробное число
у = х -1,3 , у = х -0,7 , у = х -2,12 , …
у
Функция убывает на
промежутке
х
1
0
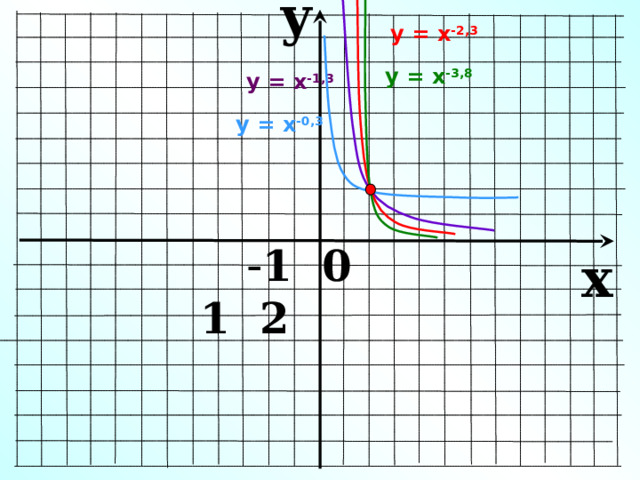
y
у = х -2,3
у = х -3,8
у = х -1,3
у = х -0,3
- 1 0 1 2
x

Домашнее задание:
1
Выучить опорный конспект.
2
Задача № 5 стр.41 Филипенко О.В. (3 уровня)
Литература: Филипенко, О. В. Математика : учебное пособие / О. В. Филипенко. https://www.iprbookshop.ru/94336.html
Материалы занятия на сайте по логину и паролю https :// videouroki . net / et / pupil

 Получите свидетельство
Получите свидетельство Вход
Вход











 Презентация "Степенные функции" (811 KB)
Презентация "Степенные функции" (811 KB)
 0
0 880
880 48
48 Нравится
0
Нравится
0





