Тема урока. Степенная функция.
Моделирование физических процессов.
(Интегрированный урок алгебры и физики в 10 классе)
Цель: способствовать формированию научного мировоззрения учеников, обеспечить усвоение свойств степенной функции, отработать умение строить графики, применять свойства при решении задач.
Показать применение метода математического моделирования в физике. Способствовать развитию аналитического, графического мышления, научить умению устанавливать математические связи различных явлений, развивать самостоятельность мышления. Формировать умения обобщать наблюдения над конкретными процессами и выражать их математическим языком в устной и письменной формах, развивать мировоззрения учеников.
Воспитывать познавательный интерес, способствовать формированию моральных, деловых качеств учеников, развивать память, логическое мышление, разговорную речь учеников.
Оборудование: карточки с заданиями ІІ блока, ІІІ блока, домашней самостоятельной работы, мультимедийная доска, компьютер, диск с презентацией урока, которую создали ученики.
ОРГАНИЗАЦИЯ УРОКА.
Ученики класса заранее ознакомлены с темой урока, они подбирали материал, который будет использован в ходе работы на уроке. В течение месяца ребята проводили исследовательскую работу: подбирали материал по истории развития понятия степенная функция, рассматривали свойства этой функции, искали примеры физических процессов, для которых математической моделью является степенная функция. В результате такой работы ученики самостоятельно объединились в 2 группы: «математики» и «физики».
За неделю до урока ученики получили творческое задание опережающего характера, им необходимо было создать математические модели при решении задач из раздела «Молекулярная физика. Газовые законы» (курс физики, 10 класс).
На уроке каждая группа сидит за своим столом, проводится групповая работа. Группы готовили материал для выступления по теме урока.
Решения задач были оформлены учителями математики и физики заранее на мультимедийной доске, ученики не были знакомы с этими решениями.
Урок проводится учителем математики.
Учитель физики руководит работой группы «физики». При решении задач физического содержания, при составлении математической модели задачи он задает вопросы, которые позволяют выяснить понимание учениками физического смысла процессов.
Блок – схема урока
І Блок. Информационно-аналитический
ІІ Блок. Исследовательский
ІІІ Блок. Познавательный
ІV Блок. Итоговый
( на экране)
І Блок. Информационно-аналитический
Перед уроком ученики получили перечень заданий, которые будут рассматриваться на уроке. Им дается возможность подготовить ответы. От каждой группы выбираются ученики, которые отвечают на поставленные вопросы. Другая группа оценивает правильность ответа. На вопросы группы отвечают поочередно.
Проводится проверка домашнего задания:
Технология «Микрофон»
Учитель задает вопросы ученикам. Ученикам предложен предмет, который будет играть роль микрофона. Отвечает тот, у кого «микрофон».
На экране проектируется график соответствующей функции, схема исследования функции, по ходу ответа ученика идет анимация, демонстрация свойств функции, после ответа одной и другой групп высвечивается правильный ответ.
Р асскажите о свойствах степенной функции с отрицательным нечетным показателем
асскажите о свойствах степенной функции с отрицательным нечетным показателем
Расскажите о свойствах степенной функции с отрицательным четным показателем
Расскажите о свойствах степенной функции с положительным иррациональным показателем меньшим 1.

Расскажите о свойствах степенной функции с иррациональным показателем большим 1.
Расскажите о свойствах степенной функции с отрицательным иррациональным показателем.

Учитель поощряет ответы учеников, подводит итоги работы групп.
ІІ Блок. Исследовательский
Ученики двух групп выбирают, кто отвечает на задания второго блока. К доске вызываются одновременно два ученика, один решает первую задачу на доске, другой работает на мультимедийной доске. Остальные ученики в группах решают задачи 3 и 4.
1. Найдите область определения функции f (x) = (10+3x-x2)-π.
2 . Установите пары. Графики, каких степенных функций изображены на чертеже.
. Установите пары. Графики, каких степенных функций изображены на чертеже.
После проверки правильности ответов вызванных учеников доски идет защита решений 3 и 4 задач.
3. Решите уравнение 
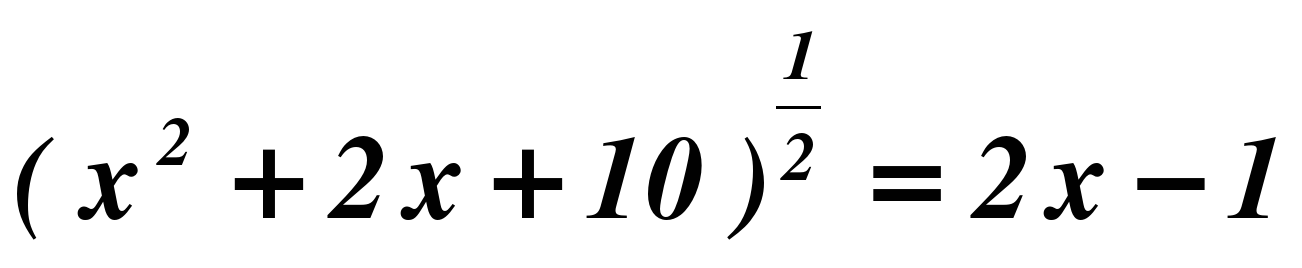 .
.
4. Схематически постройте график функции 
ІІІ Блок. Познавательный
Интерактивное задание «Мозговая атака»
Ученикам предлагается ответить на вопрос:
Обобщенная степенная функция – что мы понимаем под этим терміном? (Ученики не знакомы с таким понятим).
Ученики из группы «математики» рассказывают о математическом моделировании, об обобщенной степенной функции, её графике.
Ученики из группы «физики» знакомят класс с решением творческих заданий, оформляя их на доске, затем показываеться решение на мультимедийной доске, иногда это другой способ решения задачи.
1. Изобразить графически зависимость плотности данной массы идеального газа от температуры при постоянном давлении.
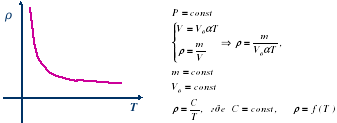
После ответа ученика решение задачи демонстрируется на экране. Ответ ученика может не совпасть с решением, которое высвечивается на мультимедйной доске, это дает возможность дискуссии. Учителя математики и физики задают вопросы для выяснения математического и физического смысла явления. Зависимость плотности данной массы газа от температуры – степенная функция с показателем р = - 1 на помежутке (0; +∞﴿, график которой – ветвь гиперболы.
2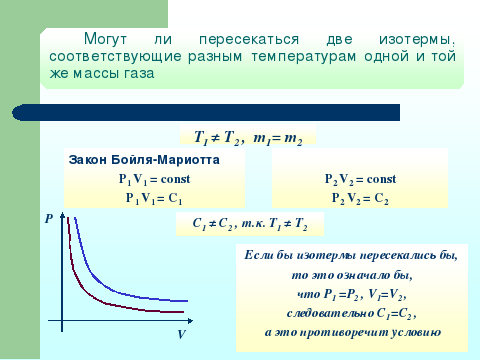 . Могут ли пересекаться две изотермы, соответствующие разным температурам одной и той же массы.
. Могут ли пересекаться две изотермы, соответствующие разным температурам одной и той же массы.
В данном примере математическая модель – степенные функции
P(V)= C1V-1, P(V)= С2V-1 с областью определения (0; +∞﴿, графики изотерм – гиперболы.
3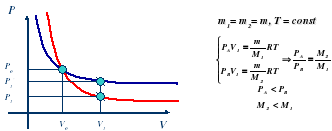 . На рисунке изображены изотермы для двух идеальных газов с одинаковыми массами и разными молярными массами, находящимися при одинаковой температуре.
. На рисунке изображены изотермы для двух идеальных газов с одинаковыми массами и разными молярными массами, находящимися при одинаковой температуре.
Пользуясь уравнением Менделеева-Клайперона, выяснить, какая гипербола относится к газу с большей молярной массой.
Нижняя гипербола относится к газу с большей молярной массой.
4. На рисунке изображены гиперболы для двух идеальных газов с одинаковыми молярными массами и разными массами, находящимися при одинаковой температуре.
Пользуясь уравнением Менделеева-Клайперона, выяснить, какая гипербола относится к газу с большей массой.
З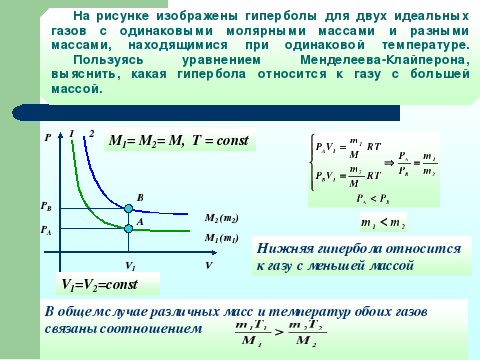 адача не предлагалась ученикам для предварительного обсуждения.
адача не предлагалась ученикам для предварительного обсуждения.
ІV Блок. Итоговый
Интерактивное задание «Незаконченное предложение»
Учитель формулирует незаконченное предложение и предлагает высказаться по подведению урока, заканчивая предложения:
«На сегодняшнем уроке мы узнали новое … »
«Сегодня для меня было открытием … »
«Мне понравилось на уроке … »
«Нам необходимо поработать над вопросами … »
Домашнее задание.
Выполнить домашнюю самостоятельную работу ( ученики получили дифференцированное задание – 4 варианта)

 Получите свидетельство
Получите свидетельство Вход
Вход




 асскажите о свойствах степенной функции с отрицательным нечетным показателем
асскажите о свойствах степенной функции с отрицательным нечетным показателем

 . Установите пары. Графики, каких степенных функций изображены на чертеже.
. Установите пары. Графики, каких степенных функций изображены на чертеже.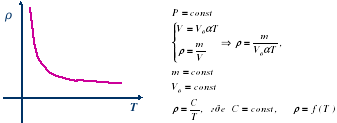
 . Могут ли пересекаться две изотермы, соответствующие разным температурам одной и той же массы.
. Могут ли пересекаться две изотермы, соответствующие разным температурам одной и той же массы. . На рисунке изображены изотермы для двух идеальных газов с одинаковыми массами и разными молярными массами, находящимися при одинаковой температуре.
. На рисунке изображены изотермы для двух идеальных газов с одинаковыми массами и разными молярными массами, находящимися при одинаковой температуре.  адача не предлагалась ученикам для предварительного обсуждения.
адача не предлагалась ученикам для предварительного обсуждения.








 Интегрированный урок математики и физики "Степенная функция. Моделирование физических процессов" (6.72 MB)
Интегрированный урок математики и физики "Степенная функция. Моделирование физических процессов" (6.72 MB)
 0
0 996
996 137
137 Нравится
0
Нравится
0


