Получите свидетельство
Вход
«Неравенства»
9 класс, подготовка к ОГЭ
2014
«Мой университет - www.moi-mummi.ru»
b , если а – b 0 Число а меньше числа b , если разность а – b – отрицательное число a , если а – b Если а – b = 0, то а = b На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее " width="640"
Число а больше числа b ,
если разность а – b – положительное число
a b , если а – b 0
Число а меньше числа b ,
если разность а – b – отрицательное число
a , если а – b
Если а – b = 0, то а = b
На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее
b и b c, a c a c b Если a b, с любое число, то a+c b+c Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство Если а b и с-положительное число ( c 0 ), то ac bc Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство Если а b и с - отрицательное число ( c 0 ), то ac b с Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число, и изменить знак неравенства на противоположный, то получится верное неравенство " width="640"
Свойства числовых неравенств :
Если a b и b c, a c
a
c
b
Если a b, с любое число, то a+c b+c
Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство
Если а b и с-положительное число ( c 0 ), то ac bc
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство
Если а b и с - отрицательное число ( c 0 ), то ac b с
Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число, и изменить знак неравенства на противоположный, то получится верное неравенство
0 ( , 0, ), где а и в – любые числа, за исключением: а ≠ 0. Квадратное неравенство – неравенство вида ах 2 +вх+с 0 ( , 0, ), где а ≠0. " width="640"
- Линейное неравенство – неравенство вида ах+в 0 ( , 0, ), где а и в – любые числа, за исключением: а ≠ 0.
- Квадратное неравенство – неравенство вида ах 2 +вх+с 0 ( , 0, ), где а ≠0.
Основные правила решения неравенств.
1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.
2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
:а
3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
: а
0 , два корня х и х D=0 , один корень х D корней нет a х ² + b х + с 1 2 2 D = b – 4ac – b D + - х = 1, 2 2a " width="640"
Алгоритм решения квадратного неравенства .
1. Находят дискриминант квадратного трехчлена ах 2 +вх+с и выясняют, имеет ли трехчлен корни;
D 0 , два корня х и х
D=0 , один корень х
D корней нет
a х ² + b х + с
1
2
2
D = b – 4ac
– b D
+
-
х =
1, 2
2a
0 или вниз при а ; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 или в нижней при а ; а а 0 а 0 а а 0 а х х х х х х х х 1 2 1 1 2 2 1 2 " width="640"
2. Если трехчлен имеет корни, то отмечают их на оси Х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а 0 или вниз при а ; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 или в нижней при а ;
а
а 0
а 0
а
а 0
а
х
х
х
х
х
х
х
х
1
2
1
1
2
2
1
2
0 или ниже оси Х (если решают неравенство ах ² +вх+с‹0 a х ² + bx + c a х ² + bx + c 0 х х х 1 х 2 1 2 " width="640"
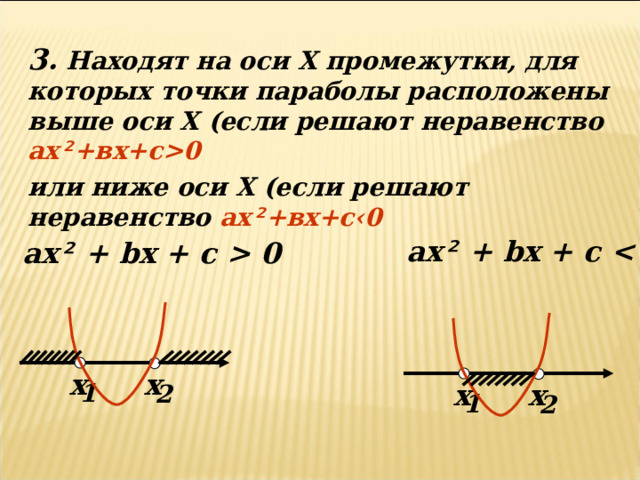
3. Находят на оси Х промежутки, для которых точки параболы расположены выше оси Х (если решают неравенство ах ² +вх+с 0
или ниже оси Х (если решают неравенство ах ² +вх+с‹0
a х ² + bx + c
a х ² + bx + c 0
х
х
х
1
х
2
1
2
Презентация" Решение неравенств, теория" (1.47 MB)
0
376
20
Нравится
0
