Презентация по теме: Призма

«Призма»

Призма —   многогранник , две грани которого являются  конгруэнтными  (равными)  многоугольниками , лежащими в параллельных плоскостях, а остальные грани —  параллелограммами , имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями

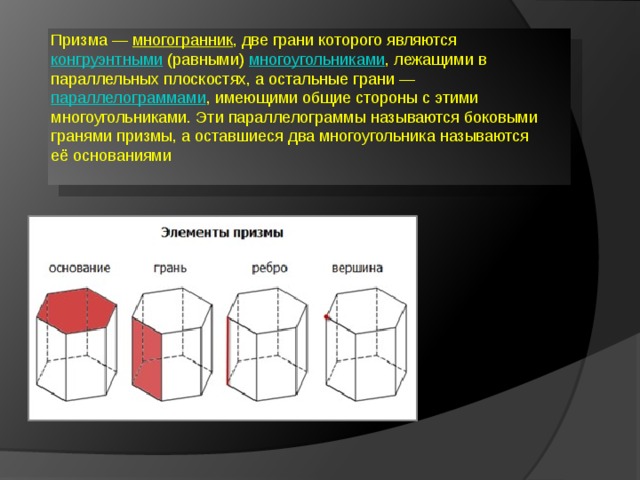
Элементы призмы

Основания   (ABCDE, KLMNP)  – 2 грани, являющиеся

конгруэнтными многоугольниками, которые лежат

в плоскостях, параллельных друг другу.

Боковые грани   (ABLK, BCML, CDNM, DEPN, EAKP)  – каждая из граней, не считая оснований. Все боковые грани – это параллелограммы.

Боковая поверхность  – сумма боковых граней.

Полная поверхность  – сумма основания и боковой

поверхности.

Боковые ребра   (AK, BL, CM, DN, EP)  – общие стороны

боковых граней.

Высота   (KR)  – отрезок, который соединяет плоскости, в них лежат основания призмы. Он перпендикулярен этим плоскостям.

Диагональ   (BP)  – отрезок, который соединяет 2 вершины призмы, которые не принадлежат одной грани.

Диагональная плоскость –  плоскость, которая проходит через боковое ребро призмы, а также диагональ основания.

Диагональное сечение   (EBLP)  – пересечение призмы и диагональной плоскости. В сечении получается параллелограмм, либо - ромб ,  прямоугольник ,  квадрат .

Перпендикулярное (ортогональное) сечение –  пересечение призмы и плоскости, перпендикулярной боковому ребру призмы.

Виды призм:

• Прямая призма  — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются  прямоугольниками . Другие призмы называются наклонными.
• Правильная призма  — это прямая призма, основанием которой является  правильный многоугольник . Боковые грани правильной призмы —  прямоугольники .
• Усечённая призма  — это призма с непараллельными основаниями.

Свойства призмы

• Основания призмы  – это равные многоугольники.
• Боковые грани  призмы имеют вид параллелограмма.
• Боковые ребра  призмы параллельные и равны.
• Площадь боковой поверхности   произвольной призмы :
•   S=P*l , где  P  — периметр перпендикулярного сечения,  l  — длина бокового ребра. 
• Площадь боковой поверхности  прямой призмы : 
• S=P*h , где  P  — периметр основания призмы,  h  — высота призмы. 
• Перпендикулярное сечение перпендикулярно всем боковым рёбрам призмы.
• Углы перпендикулярного сечения  — это линейные  углы  двугранных углов при соответствующих
• боковых рёбрах.
• Перпендикулярное сечение перпендикулярно всем боковым граням.
• Объем призмы  равен произведению площади основания призмы, на высоту. 
• Формула объема призмы:  
• V = S o *h
• где  V  - объем призмы,
• S o  - площадь основания призмы,
• h  - высота призмы.

Свойства правильной четырехугольной призмы

• Основания правильной четырехугольной призмы – это 2 одинаковых квадрата;
• Верхнее и нижнее основания параллельны;
• Боковые грани имеют вид прямоугольников;
• Все боковые грани равны между собой;
• Боковые грани перпендикулярны основаниям;
• Боковые ребра параллельны между собой и равны;
• Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям;
• Углы перпендикулярного сечения - прямые;
• Диагональное сечение правильной четырехугольной призмы является прямоугольником;
• Перпендикулярное (ортогональное сечение) параллельно основаниям.

Формулы для правильной четырехугольной призмы  

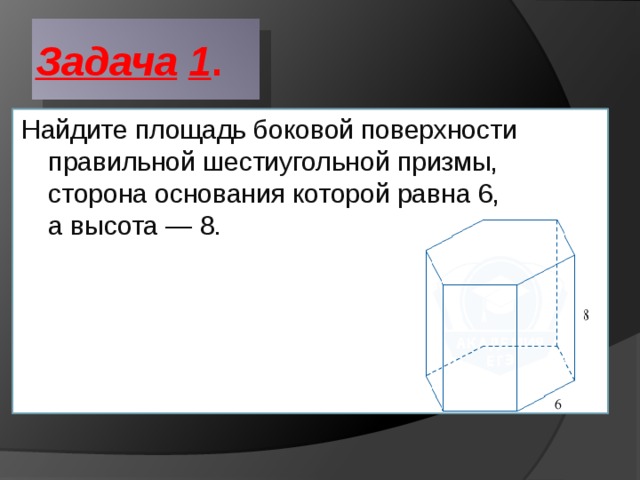
Задача 1 .

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота — 8.

Решение

Площадь боковой поверхности призмы находим по формуле  S бок. =  P осн. ·  h = 6 a ⋅ h , где  P осн.  и  h  — соответственно периметр основания и высота призмы, равная 8, и  a  — сторона правильного шестиугольника, равная 6. Следовательно,  S бок.  = 6⋅6⋅8 = 288.

Ответ:

288

Задача 2

В правильной треугольной призме  ABCA ​1​​ B ​1​​ C ​1​​ стороны основания равны 4, а боковые рёбра равны 10. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC,A1B1 и A1C1

Решение

Рассмотрим следующий рисунок.

Отрезок  MN  является средней линией треугольника  A ​1​​ B ​1​​ C ​1​​, поэтому MN = 1:2 B1C1 =2.  Кроме того, MK = NL = 10. MK = NL =10. Отсюда следует, что четырёхугольник  MNLK  является параллелограммом. Так как MK ll AA1, то  MK ⊥ ABC  и  MK ⊥ KL . Следовательно, четырёхугольник  MNLK  является прямоугольником.  S ​ MNLK ​​= MK ⋅ KL =10⋅2= 20.20.

Ответ

20