
Многогранники. Призма.
Тема
http://lapinagv.jimdo.com/

Двугранные углы. Линейный угол.
Тема урока
http://lapinagv.jimdo.com/
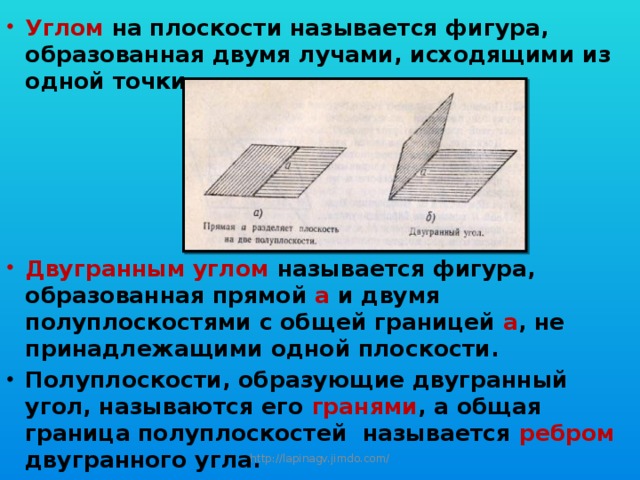
- Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки.
- Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а , не принадлежащими одной плоскости.
- Полуплоскости, образующие двугранный угол, называются его гранями , а общая граница полуплоскостей называется ребром двугранного угла.
http://lapinagv.jimdo.com/

Предметы, имеющие форму двугранного угла
http://lapinagv.jimdo.com/
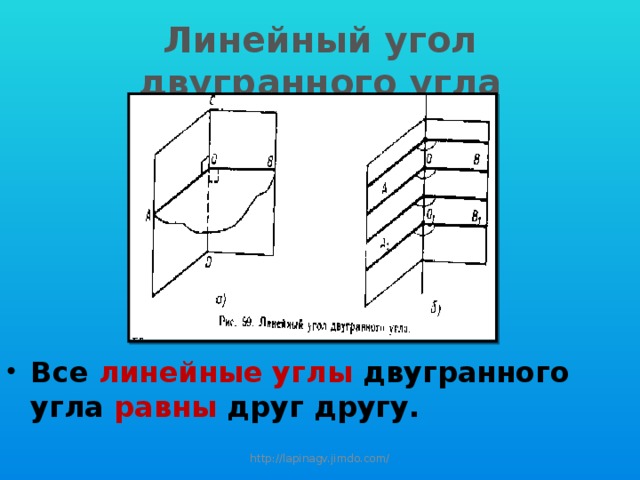
Линейный угол двугранного угла
- Все линейные углы двугранного угла равны друг другу.
http://lapinagv.jimdo.com/
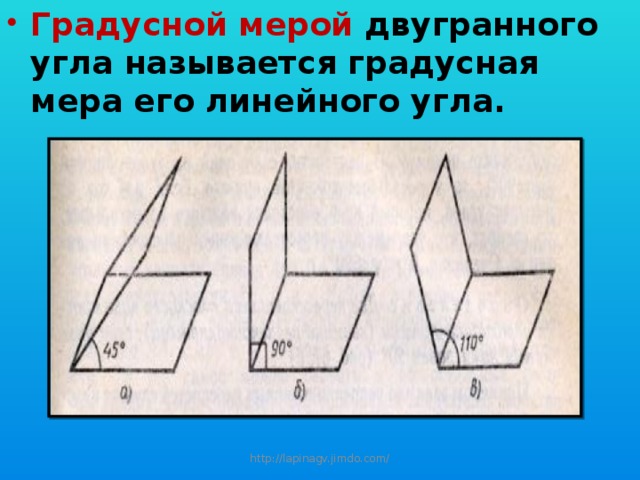
- Градусной мерой двугранного угла называется градусная мера его линейного угла.
http://lapinagv.jimdo.com/

Многогранник и его элементы.
Тема урока
http://lapinagv.jimdo.com/

- Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников .
- Многоугольники, из которых составлен многогранник, называются его гранями .
- Стороны граней называются рёбрами , концы рёбер – вершинами многогранника.
- Отрезок, соединяющий две вершины, не принадлежащие одной грани, называются диагональю многогранника.
http://lapinagv.jimdo.com/

Симметрия в пространстве
- Фигура может иметь один или несколько центров симметрии.
- С симметрией часто встречаемся в природе, архитектуре, технике, быту.
http://lapinagv.jimdo.com/

- Многие здания симметричны относительно плоскости, например главное здание Московского государственного университета.
- Почти все кристаллы, встречающиеся в природе, имеют центр, ось или плоскость симметрии.
- В геометрии центр, ось и плоскость симметрии многогранника называются элементами симметрии этого многогранника.
http://lapinagv.jimdo.com/

Симметрия в архитектуре
http://lapinagv.jimdo.com/

http://lapinagv.jimdo.com/
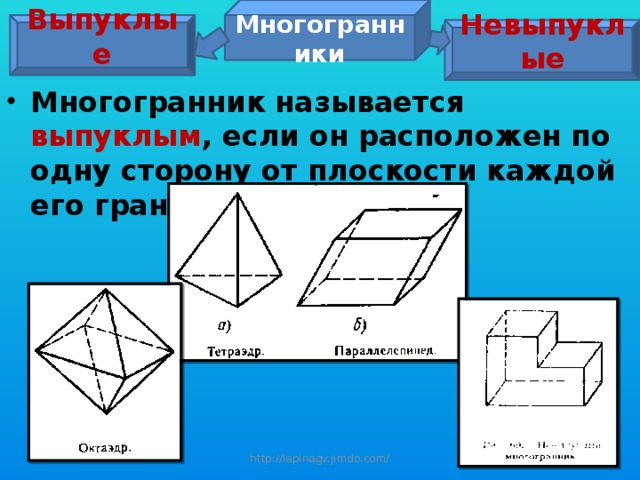
Многогранники
- Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани.
Выпуклые
Невыпуклые
http://lapinagv.jimdo.com/

Выпуклый многогранник называется правильным , если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер.
http://lapinagv.jimdo.com/
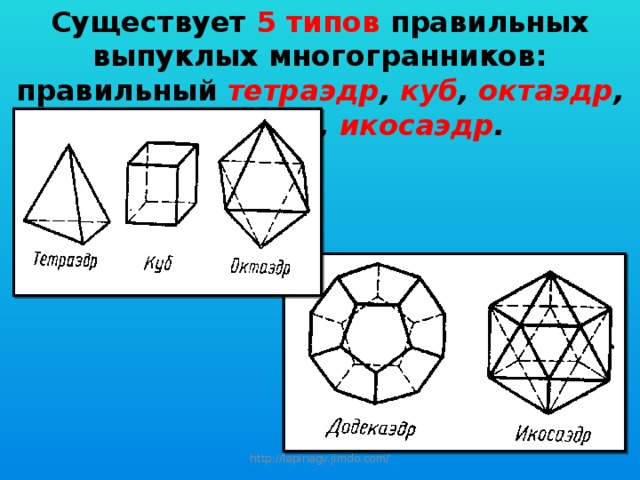
Существует 5 типов правильных выпуклых многогранников: правильный тетраэдр , куб , октаэдр , додекаэдр , икосаэдр .
http://lapinagv.jimdo.com/

Правильный тетраэдр
- Составлен из четырех равносторонних треугольников.
- Каждая его вершина является вершиной трех треугольников.
http://lapinagv.jimdo.com/

Правильный октаэдр
- Составлен из восьми равносторонних треугольников.
- Каждая вершина октаэдра является вершиной четырех треугольников.
http://lapinagv.jimdo.com/

Правильный икосаэдр
- Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно сумма плоских углов при каждой вершине равна 300 °.
http://lapinagv.jimdo.com/

Куб
- Составлен из шести квадратов.
- Каждая вершина куба является вершиной трех квадратов.
http://lapinagv.jimdo.com/

Правильный додекаэдр
- Составлен из двенадцати правильных пятиугольников.
- Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.
http://lapinagv.jimdo.com/
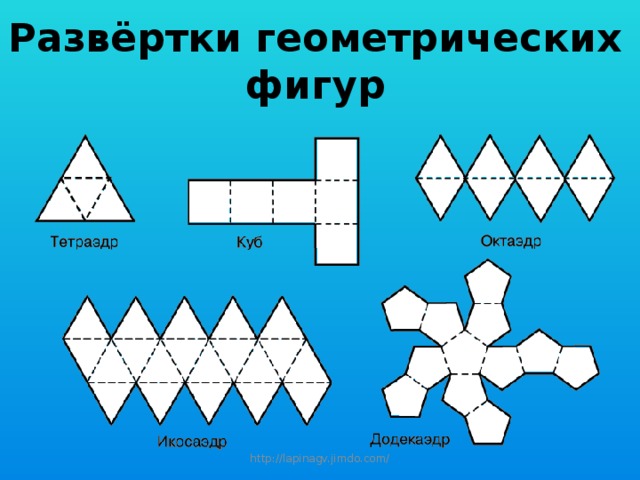
Развёртки геометрических фигур
http://lapinagv.jimdo.com/

Призма и её элементы.
Тема урока
http://lapinagv.jimdo.com/
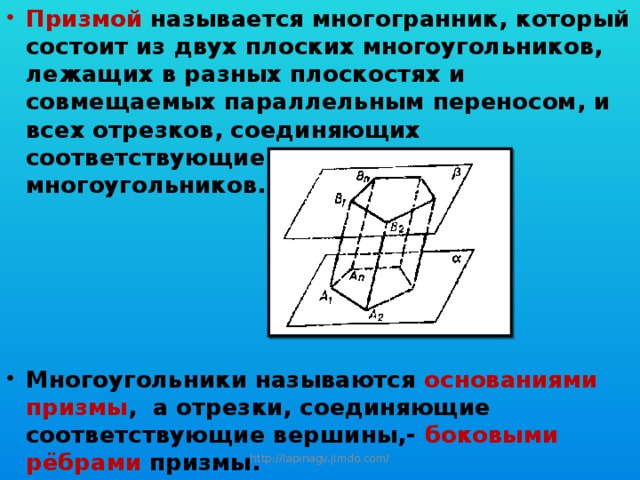
- Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
- Многоугольники называются основаниями призмы , а отрезки, соединяющие соответствующие вершины,- боковыми рёбрами призмы.
http://lapinagv.jimdo.com/
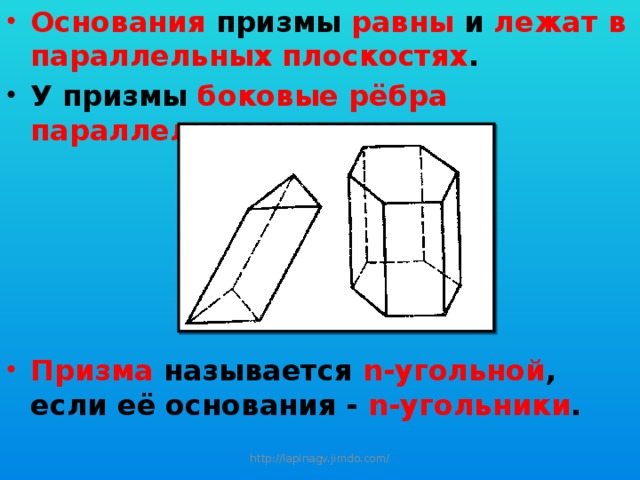
- Основания призмы равны и лежат в параллельных плоскостях .
- У призмы боковые рёбра параллельны и равны .
- Призма называется n-угольной , если её основания - n-угольники .
http://lapinagv.jimdo.com/

Задание №1
а) 9 вершин; в) 14 рёбер;
б) 16 вершин; г) 17 рёбер?
2) Какой многоугольник лежит в основании призмы, которая имеет 15 рёбер?
3) Определите вид призмы, которая имеет:
а) 10 вершин;
б) 18 рёбер;
в) 8 граней.
http://lapinagv.jimdo.com/

Задание №2
На рисунке найдите фигуры, которые являются развёртками призм. Определите вид этих призм.
http://lapinagv.jimdo.com/
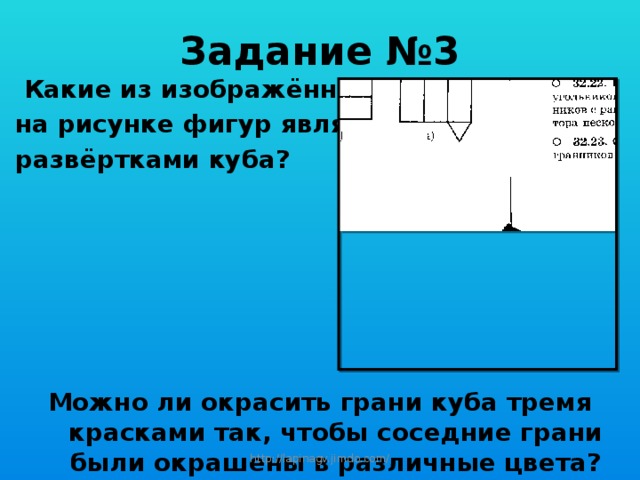
Задание №3
Какие из изображённых
на рисунке фигур являются
развёртками куба?
Можно ли окрасить грани куба тремя красками так, чтобы соседние грани были окрашены в различные цвета?
http://lapinagv.jimdo.com/
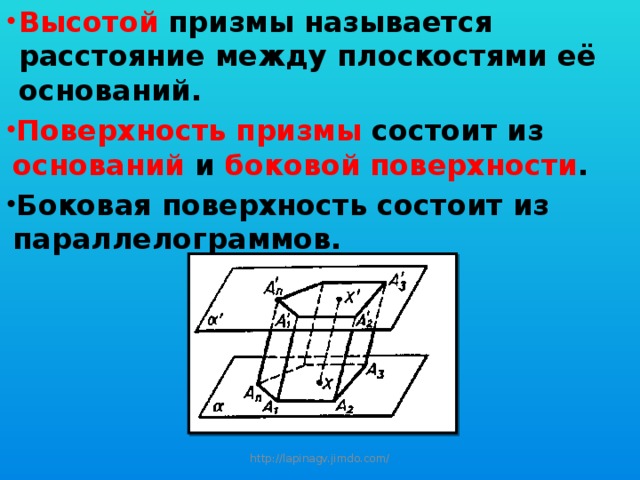
- Высотой призмы называется расстояние между плоскостями её оснований.
- Поверхность призмы состоит из оснований и боковой поверхности .
- Боковая поверхность состоит из параллелограммов.
http://lapinagv.jimdo.com/
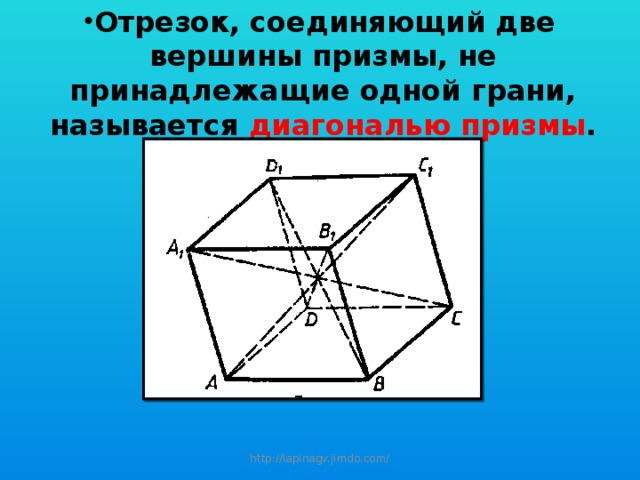
- Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы .
http://lapinagv.jimdo.com/

Самостоятельная работа
- Изобразите треугольную и четырёхугольную призмы.
- Обозначьте их, проведите диагонали и высоты, выпишите все элементы:
- вершины ;
- основания ;
- боковые рёбра ;
- боковые грани ;
- высоты ;
- диагонали .
http://lapinagv.jimdo.com/

Диагональное сечение призмы.
Тема урока
http://lapinagv.jimdo.com/
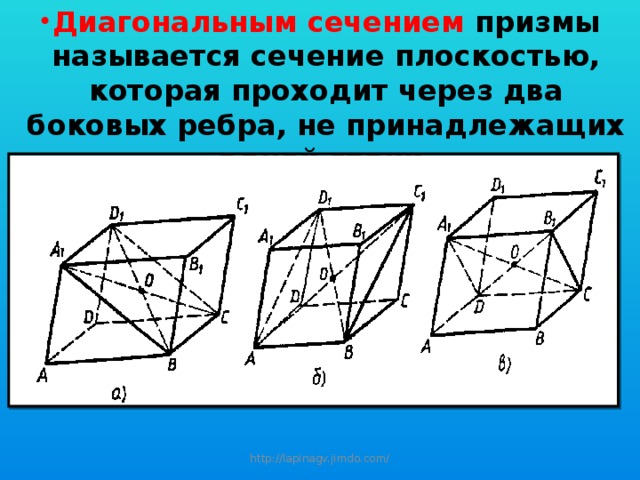
- Диагональным сечением призмы называется сечение плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.
http://lapinagv.jimdo.com/

Сечения в жизни человека.
http://lapinagv.jimdo.com/
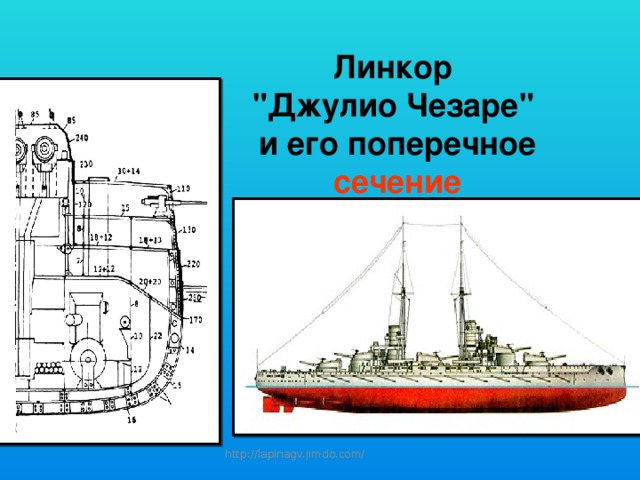
Линкор "Джулио Чезаре" и его поперечное сечение
http://lapinagv.jimdo.com/

Трос биметалический (сечение)
http://lapinagv.jimdo.com/

Вид внутренности дома в сечении.
http://lapinagv.jimdo.com/

План крепости. Сечение по первому этажу
http://lapinagv.jimdo.com/
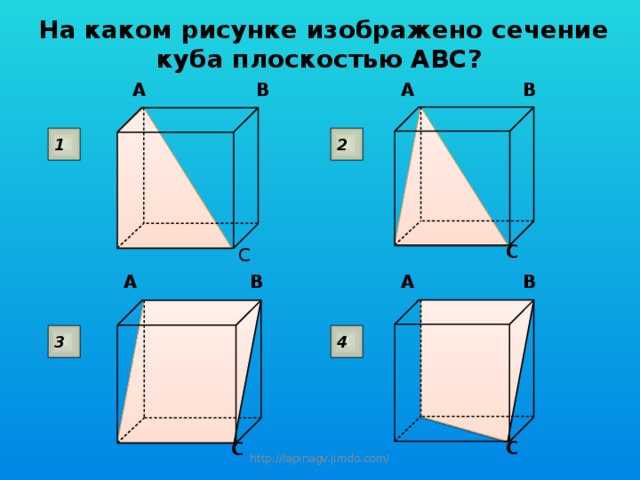
На каком рисунке изображено сечение куба плоскостью ABC?
B
A
B
A
2
1
C
C
A
B
B
A
3
4
C
C
http://lapinagv.jimdo.com/
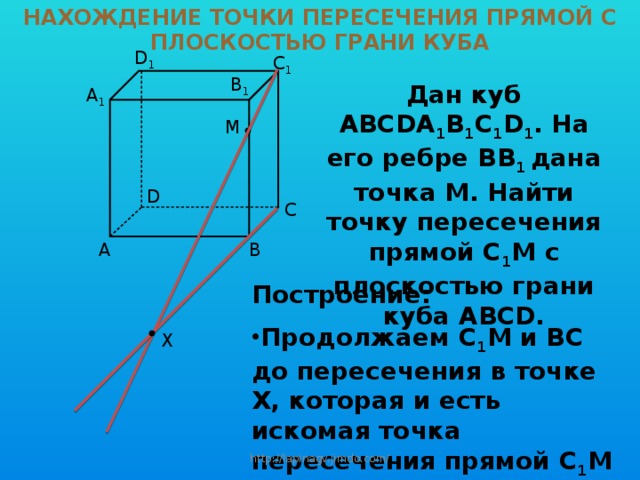
НАХОЖДЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ ГРАНИ КУБА
D 1
C 1
B 1
Дан куб ABCDA 1 B 1 C 1 D 1 . На его ребре ВВ 1 дана точка M. Найти точку пересечения прямой C 1 M с плоскостью грани куба ABCD.
A 1
M
D
C
B
A
Построение:
- Продолжаем C 1 M и BC до пересечения в точке X, которая и есть искомая точка пересечения прямой C 1 M с плоскостью грани ABCD.
X
http://lapinagv.jimdo.com/
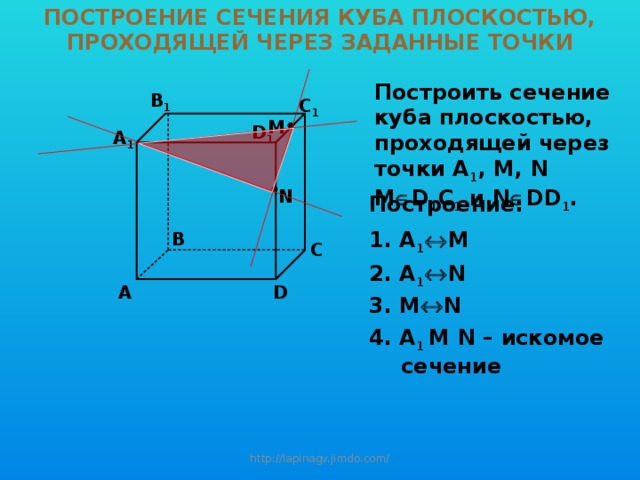
ПОСТРОЕНИЕ СЕЧЕНИЯ КУБА ПЛОСКОСТЬЮ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ЗАДАННЫЕ ТОЧКИ
Построить сечение куба плоскостью, проходящей через точки A 1 , М, N M D 1 C 1 и N DD 1 .
B 1
C 1
M
D 1
A 1
N
Построение:
1. A 1 M
B
C
2. A 1 N
D
A
3. M N
4. A 1 M N – искомое сечение
http://lapinagv.jimdo.com/
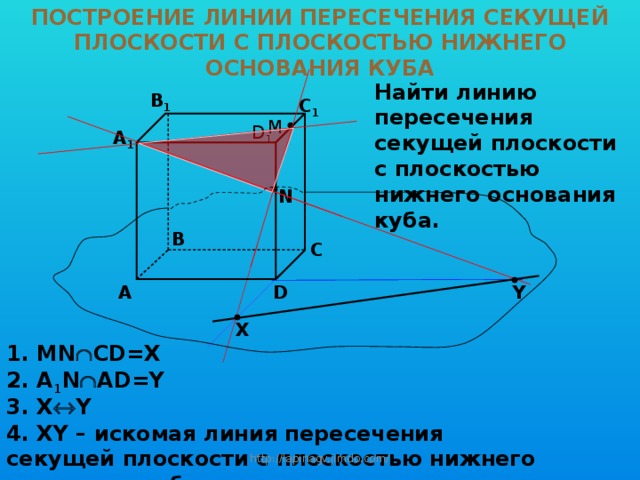
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ СЕКУЩЕЙ ПЛОСКОСТИ С ПЛОСКОСТЬЮ НИЖНЕГО ОСНОВАНИЯ КУБА
Найти линию пересечения секущей плоскости с плоскостью нижнего основания куба.
B 1
C 1
M
D 1
A 1
N
B
C
Y
A
D
X
1. MN CD=X
2. A 1 N AD=Y
3. X Y
4. XY – искомая линия пересечения секущей плоскости с плоскостью нижнего основания куба
http://lapinagv.jimdo.com/
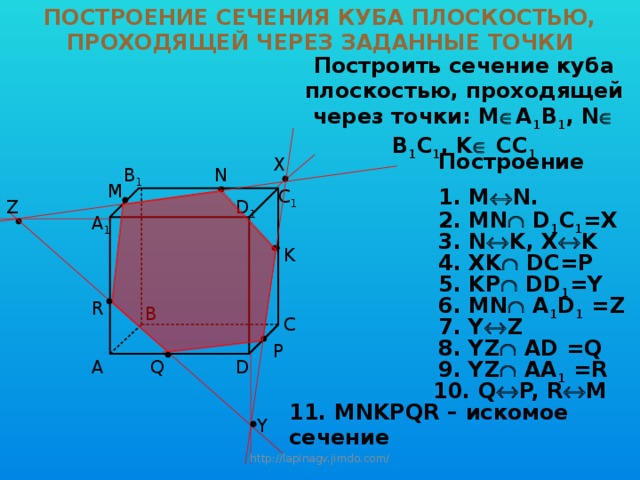
ПОСТРОЕНИЕ СЕЧЕНИЯ КУБА ПЛОСКОСТЬЮ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ЗАДАННЫЕ ТОЧКИ
Построить сечение куба плоскостью, проходящей через точки: М A 1 В 1 , N B 1 C 1 , K CC 1
Построение
1. M N.
X
N
B 1
M
C 1
Z
D 1
2. MN D 1 C 1 =X
A 1
3. N K, X K
K
4. XK DC=P
5. KP DD 1 =Y
6. MN A 1 D 1 =Z
R
B
7. Y Z
C
8. YZ AD =Q
P
9. YZ AA 1 =R
D
A
Q
10. Q P, R M
11. MNKPQR – искомое сечение
Y
http://lapinagv.jimdo.com/

Задание №1
Сечение правильной треугольной призмы АВСА’B’C’ проходит через ребро АВ и точку пересечения диагоналей грани АСС’А’ . Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
http://lapinagv.jimdo.com/
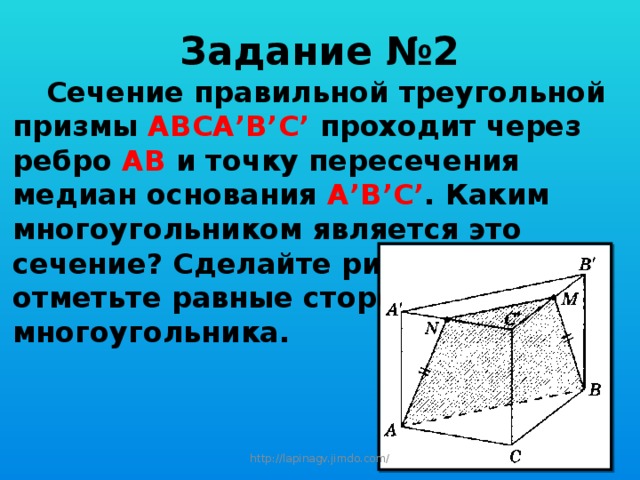
Задание №2
Сечение правильной треугольной призмы АВСА’B’C’ проходит через ребро АВ и точку пересечения медиан основания А’В’С’ . Каким многоугольником является это сечение? Сделайте рисунок и отметьте равные стороны этого многоугольника.
http://lapinagv.jimdo.com/
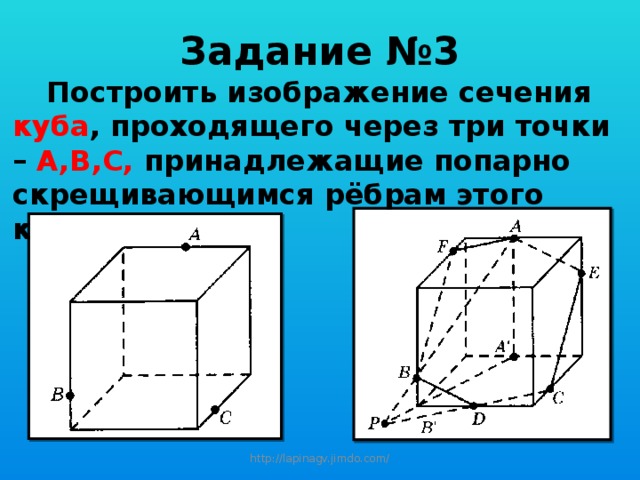
Задание №3
Построить изображение сечения куба , проходящего через три точки – А,В,С, принадлежащие попарно скрещивающимся рёбрам этого куба.
http://lapinagv.jimdo.com/

Прямая, наклонная и правильная призма.
Тема урока
http://lapinagv.jimdo.com/
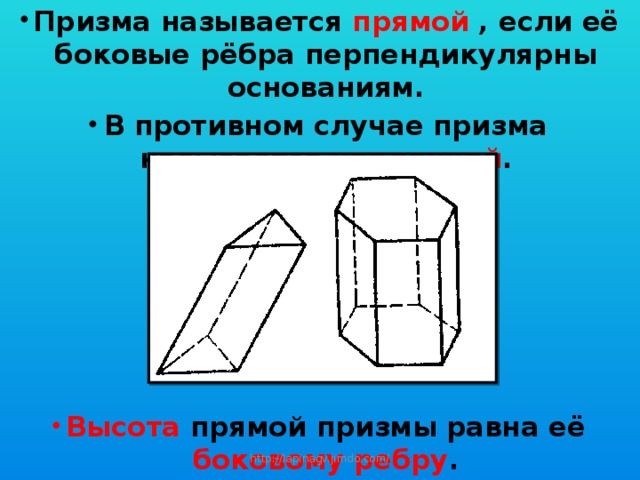
- Призма называется прямой , если её боковые рёбра перпендикулярны основаниям.
- В противном случае призма называется наклонной .
- Высота прямой призмы равна её боковому ребру .
http://lapinagv.jimdo.com/
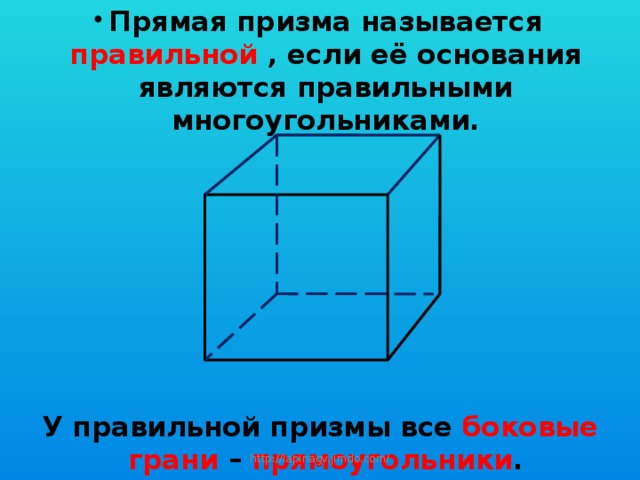
- Прямая призма называется правильной , если её основания являются правильными многоугольниками.
У правильной призмы все боковые грани – прямоугольники .
http://lapinagv.jimdo.com/
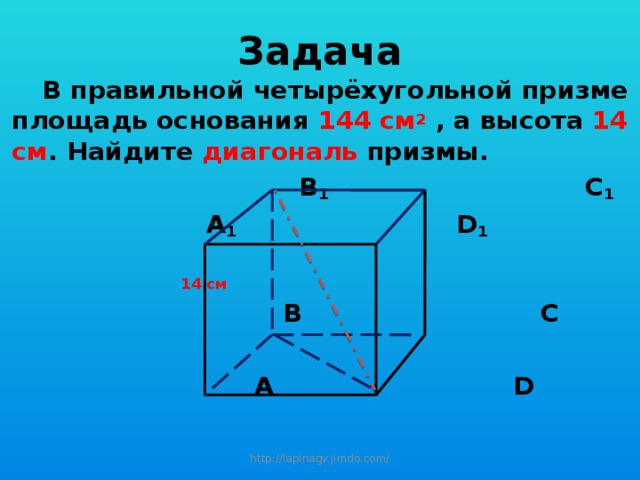
Задача
В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см . Найдите диагональ призмы.
В 1 С 1
А 1 D 1
14 см
B C
А D
http://lapinagv.jimdo.com/

Параллелепипед, его свойства.
Тема урока
http://lapinagv.jimdo.com/
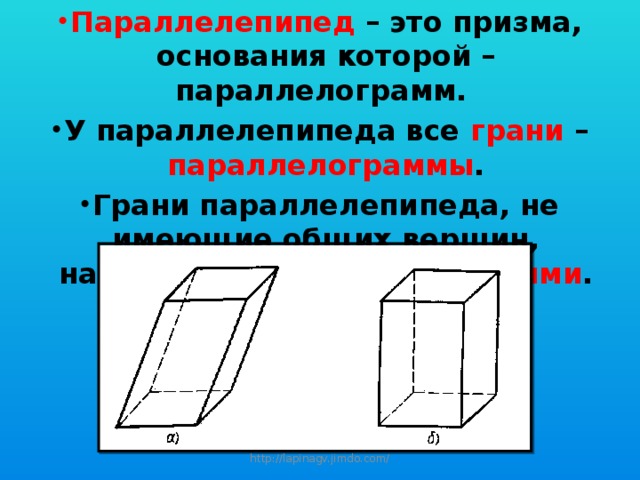
- Параллелепипед – это призма, основания которой – параллелограмм.
- У параллелепипеда все грани – параллелограммы .
- Грани параллелепипеда, не имеющие общих вершин, называются противолежащими .
http://lapinagv.jimdo.com/
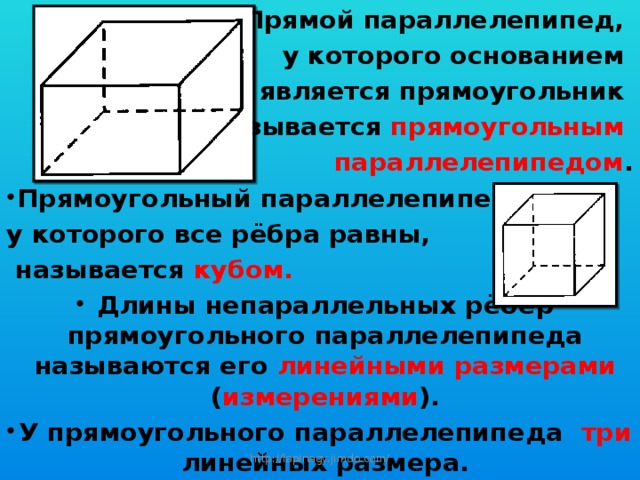
у которого основанием
является прямоугольник
называется прямоугольным
параллелепипедом .
- Прямоугольный параллелепипед,
у которого все рёбра равны,
называется кубом.
- Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами ( измерениями ).
- У прямоугольного параллелепипеда три линейных размера.
http://lapinagv.jimdo.com/
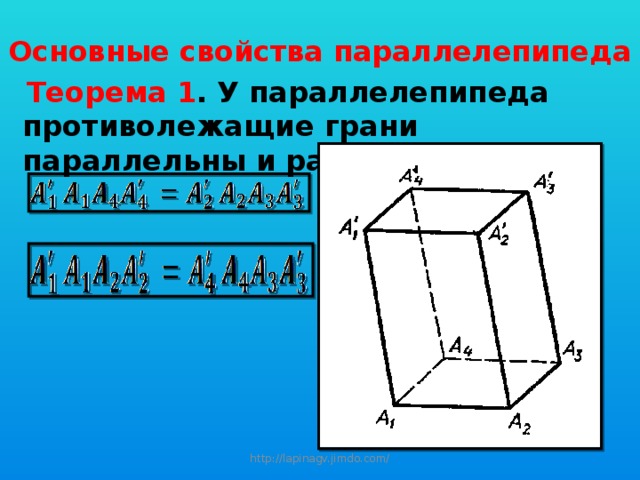
Основные свойства параллелепипеда
Теорема 1 . У параллелепипеда противолежащие грани параллельны и равны.
http://lapinagv.jimdo.com/
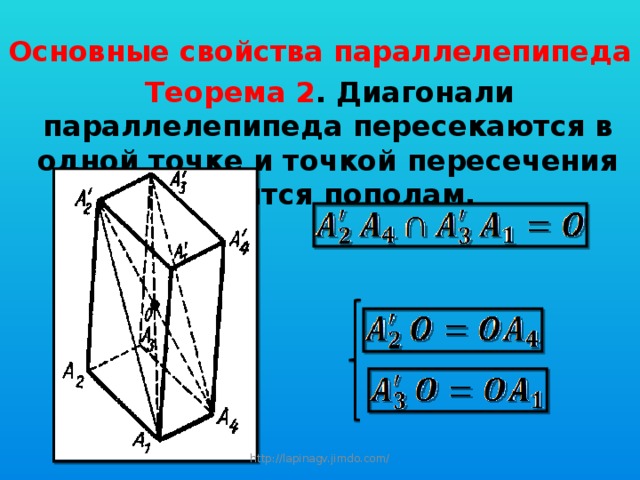
Основные свойства параллелепипеда
Теорема 2 . Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
http://lapinagv.jimdo.com/
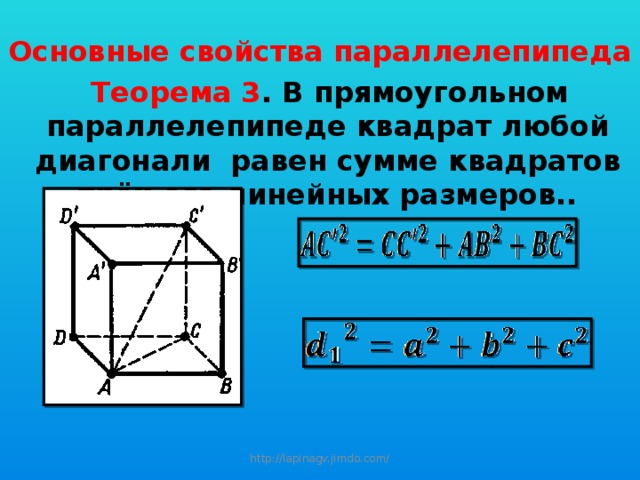
Основные свойства параллелепипеда
Теорема 3 . В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его линейных размеров..
http://lapinagv.jimdo.com/
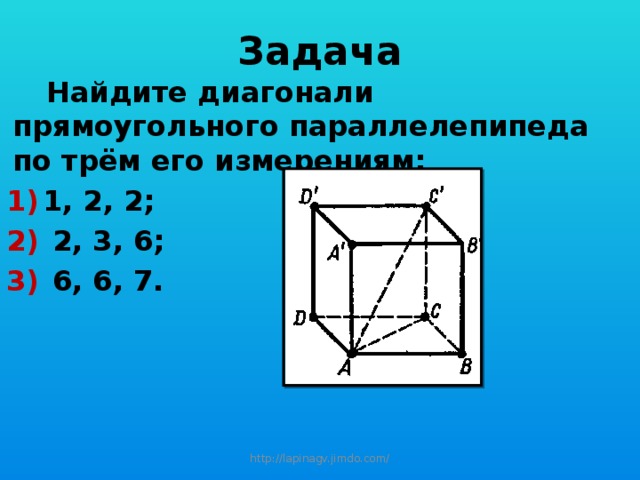
Задача
Найдите диагонали прямоугольного параллелепипеда по трём его измерениям:
- 1, 2, 2;
- 2, 3, 6;
- 6, 6, 7.
http://lapinagv.jimdo.com/

Понятие площади. Площадь боковой поверхности призмы.
Тема урока
http://lapinagv.jimdo.com/

- Фигуру называют простой если её можно разбить на конечное число плоских треугольников.
- Площадь – это положительная
величина, численное значение которой обладает следующими свойствами:
- 1) Равные фигуры имеют равные площади.
- 2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей его частей.
- 3) Площадь квадрата со стороной, равной единице измерения, равна единице.
http://lapinagv.jimdo.com/

Упражнение
- 1. Как изменится площадь квадрата, если увеличить в 3 раза каждую его сторону?
- 2. Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
http://lapinagv.jimdo.com/

- Боковой поверхностью призмы называется сумма площадей боковых граней.
a 1 a 2 a 3
S бок =a 1 l+a 2 l+a 3 l=(a 1 +a 2 +a 3 )l=pl
l l l l
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы , т.е. на длину бокового ребра.
S бок =pl=ph
p –периметр основания призмы;
l – длина боковых рёбер;
h – высота призмы.
http://lapinagv.jimdo.com/

Задача
В прямой треугольной призме все рёбра равны. Боковая поверхность равна 12 м 2 . Найдите высоту.
http://lapinagv.jimdo.com/

Площадь полной поверхности призмы.
Тема урока
http://lapinagv.jimdo.com/

- Площадью полной поверхности призмы называется сумма площадей всех её граней.
S пол =S бок +2S осн
http://lapinagv.jimdo.com/

Задача
1. У параллелепипеда три грани имеют площади 1 м 2 , 2 м 2 , 3 м 2 . Чему равна полная поверхность параллелепипеда?
2. Найдите поверхность прямоугольного параллелепипеда по трём его измерениям:
10 см , 22 см , 16 см.
http://lapinagv.jimdo.com/

Понятие объёма. Объём призмы.
Тема урока
http://lapinagv.jimdo.com/

- Тело называют простым если его можно разбить на конечное число
треугольных пирамид.
- Объём – это положительная
величина, численное значение которой обладает следующими свойствами:
- 1) Равные тела имеют равные объёмы.
- 2) Если тело разбито на части, являющиеся простыми телами, то объём этого тела равна сумме объёмов его частей.
- 3) Объём куба, ребро которого равно единице длины, равен единице.
http://lapinagv.jimdo.com/

Объём прямоугольного параллелепипеда вычисляется по формуле:
V=abc
Объём любого прямоугольного параллелепипеда равен произведению площади егооснования на высоту:
V=S осн H
http://lapinagv.jimdo.com/

Объём любой призмы равен произведению площади основания на высоту:
V=S осн H
http://lapinagv.jimdo.com/

Задача
Боковая поверхность правильной четырёхугольной призмы равна 32 м 2 , а полная поверхность 40 м 2 . Найдите высоту и объём призмы.
http://lapinagv.jimdo.com/

Решение задач.
Тема урока
http://lapinagv.jimdo.com/

Задача
1. Три латунных куба с рёбрами 3 см , 4 см и 5 см переплавлены в один куб. Какую длину имеет ребро этого куба?
2. Требуется установить резервуар для воды ёмкостью 10 м 3 на прямоугольной площадке размером 2,5*1,75 м , служащий для него дном. Найдите высоту резервуара?
http://lapinagv.jimdo.com/

Зачёт (лабораторно – практическая работа) по теме: «Многогранники. Призма».
C 1
D 1
A 1
B 1
Тема урока
D
C
A
B
http://lapinagv.jimdo.com/

План выполнения работы:
- Определить вид данной фигуры.
- Определить необходимые измерения для уточнения вида фигуры.
- Записать формулы вычисления периметра и площади основания данной фигуры.
- Записать формулу вычисления боковой поверхности данной фигуры.
- Записать формулу вычисления полной поверхности данной фигуры.
- Записать формулу для вычисления объёма данной фигуры.
- Произвести непосредственные измерения соответствующих элементов.
- Вычислить периметр основания данной фигуры.
- Вычислить площадь боковой поверхности фигуры.
- Вычислить площадь основания данной фигуры.
- Вычислить площадь полной поверхности фигуры.
- Вычислить объём тела.
http://lapinagv.jimdo.com/


 Получите свидетельство
Получите свидетельство Вход
Вход




















































































 Многогранники. Призма (3.14 MB)
Многогранники. Призма (3.14 MB)
 2
2 5438
5438 345
345









В правом верхнем углу сайта есть форма для подписки сразу после которой вы получите код для скачивания