Филиал боу СПО «ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ» минздравсоцразвития чувашии Г. КАНАШ чувашской республики
«Утверждаю»
зав учебной части
Филиал
БОУ СПО «ЧМК»
г. Канаш
_______Фадеева Т.Э
«____» ________2014 г.
Методическая разработка
Теоретического занятия по дисциплине ОДБ.06 Математика
«Двугранный угол. Многогранные углы»
Для специальности:
060501 «Сестринское дело»
Разработала преподаватель
математики и физики
Cеменова А.М
Рассмотрена
на заседании ЦМК ОГСЭ
дисциплин
протокол №____
«____» _______2014 г
Председатель ЦМК
_________ Романова Л.В
Канаш 2014 г.
Пояснительная записка
Методическая теоретического занятия по дисциплине «Математика» на тему «Двугранный угол. Многогранные углы» составлена на основе Рабочей программы по математике и календарно-тематического плана.
Программный материал данного занятия базируется на знаниях математики. Рассматриваются вопросы:
- Двугранный угол. Трехгранный угол. Многогранные углы.
- Многогранники.
Методическая разработка занятия составлена для проведения теоретических занятий по теме: «Двугранный угол. Многогранные углы» - 2 часа, по математике для студентов 1 года обучения.
Аннотация
Методическая разработка теоретического занятия включает программный теоретический материал раздела «Многогранники», материал для изучения основные понятия в стереометрии: двугранный угол, трехгранные углы, многогранные углы, многогранники, призма, параллелипипед, куб, пирамида, правильные многогранники студентами и оценка их знаний, вопросы и упражнения для закрепления теоретического занятия.
Методическая разработка теоретического занятия по теме «Двугранный угол» рекомендуется к использованию преподавателям математики и студентам 1 года обучения.
Филиал БОУ СПО «Чебоксарский медицинский колледж» в г. Канаш
План теоретического занятия.
Специальность: 060501 Дисциплина ОДБ. 06 Математика
Тема: «Двугранный угол. Многогранные углы. Многогранники»
Тип занятия: Урок усвоения навыков и умений, комбинированное занятие – с элементами беседы и выполнением упражнений.
Цели занятия:
Образовательные - формирование знаний в усвоении понятия в изучении: Двугранный угол. Многогранные углы. Многогранники. Призма. Продолжить систематическое изучение многогранников в ходе решения задач на вычисления их.
Развивающие - развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.
Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения. Воспитывать сознательное отношение к учебе и заинтересованность
Средства обучения:
- Методическая разработка по теме.
- Электронная презентация по теме.
- Персональный компьютер, медиапроектор.
Внутрипредметные связи: Двугранный угол, многогранники, синус, косинус и тангенс числа.
Межпредметные связи: геометрия, алгебра.
Студент должен знать:
- Определение двугранного угла, трехганного и мнгогранного угла, определение призмы.
Студент должен уметь:
- решать задачи на нахождения высоты, двугранного угла при основании, ребра мнгогранников.
План занятия
1.Организационный момент – 2 мин.
2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.
3.Проверка домашнего задания – 10 мин.
4.Изучение нового материала - 35 мин.
Основной материал, с использованием электронной презентацией по теме: «Мнгогранники»
5.Закрепление материала: Решение задач № 1-2, 17,18,20 на стр 66-67. – 35 мин.
6.Подведение итогов – 3 мин.
7. Домашнее задание – 2 мин. § 5(20) Упражнение № 19,33,38.
Ход урока:
1. Организационный момент .
2. Вводная мотивация: постановка целей, изложение плана урока.
3. Проверка домашнего задания: Письменно на доске решить № 69 § 19.
4. Изучение нового материала:
Двугранный угол.
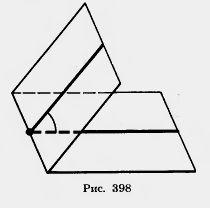
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой (рис. 398). Полуплоскости называются гранями, а ограничивающая их прямая — ребром двугранного угла.
Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным углом двугранного угла.
За меру двугранного угла принимается мера соответствующего ему линейного угла. Все линейные углы двугранного угла совмещаются параллельным переносом, а значит, равны. Поэтому мера двугранного угла не зависит от выбора линейного угла.
 Задача (1). Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА1 и ВВ1 на ребро угла. Найдите длину отрезка АВ, если АА1=а, ВВ1=b, A1B1=c и двугранный угол равен
Задача (1). Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА1 и ВВ1 на ребро угла. Найдите длину отрезка АВ, если АА1=а, ВВ1=b, A1B1=c и двугранный угол равен 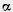 (рис. 399).
(рис. 399).
Решение. Проведем прямые А1СllВВ1 и ВСllА1В1. Четырехугольник A1B1ВС — параллелограмм, значит А1С = ВВ1 = b. Прямая A1B1 перпендикулярна плоскости треугольника АА1С1 так как она перпендикулярна двум прямым в этой плоскости АА1 и СА1.
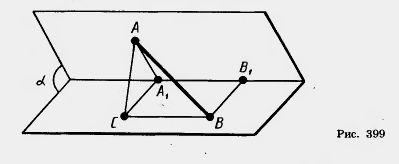
Следовательно, параллельная ей прямая ВС тоже перпендикулярна этой плоскости. Значит, треугольник ABC — прямоугольный с прямым углом С. По теореме косинусов
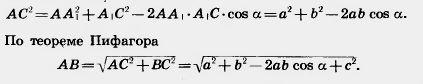
Трехгранный и многогранный угол
Рассмотрим три луча a, b, с, исходящие из одной точки и не лежащие в одной плоскости. Трехгранным углом (аbс) называется фигура, составленная из трех плоских углов (аb), (bс) и (aс) (рис. 400). Эти углы называются гранями трехгранного угла, а их стороны — ребрами . Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
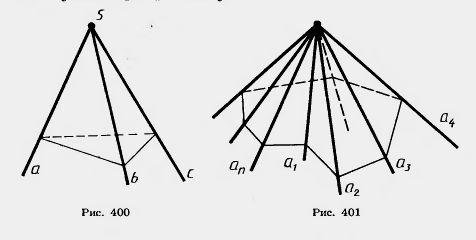
Аналогично определяется понятие многогранного угла (рис. 401).
Задача (2). У трехгранного угла (аЬс) двугранный угол при ребре с прямой, двугранный угол при ребре Ь равен 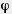 , а плоский угол (bс) равен
, а плоский угол (bс) равен 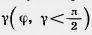 Найдите два других плоских угла:
Найдите два других плоских угла: 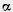 =
=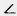 (аb),
(аb), 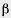 =
=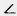 (ac).
(ac).
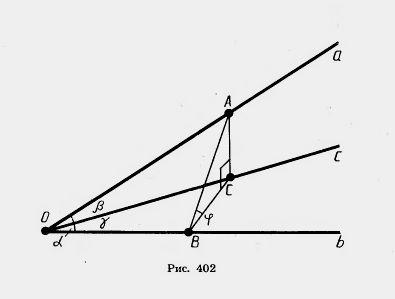
Решение. Опустим из произвольной точки А ребра a перпендикуляр АВ на ребро b и перпендикуляр АС на ребро с (рис. 402). По теореме о трех перпендикулярах СВ — перпендикуляр к ребру b.
Из прямоугольных треугольников: ОАВ, ОСВ, АОС 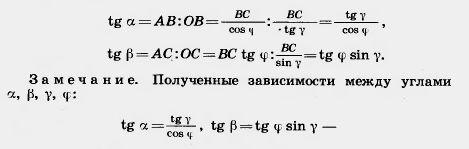 и ABC получаем:
и ABC получаем:
— позволяют, зная два угла, найти два других.
Многогранник
В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
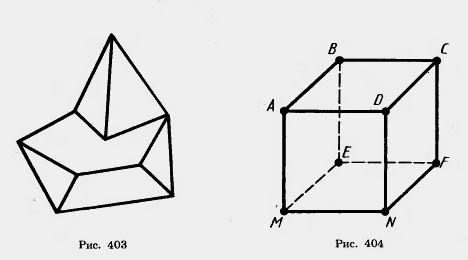
(рис. 403). Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины — вершинами многогранника.
Поясним сказанное на примере знакомого вам куба (рис. 404). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, .... Они являются его гранями. Ребрами куба являются стороны этих квадратов: АВ, ВС, BE,.... Вершинами куба являются вершины квадратов: А, В, С, D, Е, ....У куба шесть граней, двенадцать ребер и восемь вершин.
Простейшим многогранникам — призмам и пирамидам, которые будут основным объектом нашего изучения,— мы дадим такие определения, которые, по существу, не используют понятие тела. Они будут определены как геометрические фигуры с указанием всех принадлежащих им точек пространства. Понятие геометрического тела и его поверхности в общем случае будет дано позже.
Прямая призма
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально (рис. 410).
Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 19.1. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Доказательство. Боковые грани прямой призмы — прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна
S = a1l + a2l + ... + anl = pl,
где a1,аn — длины ребер основания, р — периметр основания призмы, а I — длина боковых ребер. Теорема доказана.
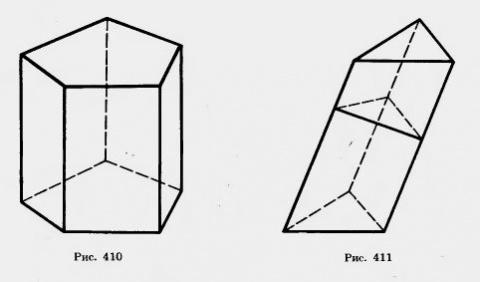
Задача (22). В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l.
Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
5.Закрепление материала: Решение задач № 1-2, 17,18,20 на стр 66-67.
6.Подведение итогов.
7. Домашнее задание. § 5(20) Упражнение № 19,33,38..
![]() (рис. 399).
(рис. 399).

 Получите свидетельство
Получите свидетельство Вход
Вход



 Задача (1). Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА1 и ВВ1 на ребро угла. Найдите длину отрезка АВ, если АА1=а, ВВ1=b, A1B1=c и двугранный угол равен
Задача (1). Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА1 и ВВ1 на ребро угла. Найдите длину отрезка АВ, если АА1=а, ВВ1=b, A1B1=c и двугранный угол равен 
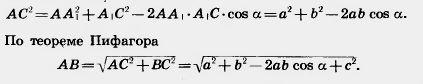


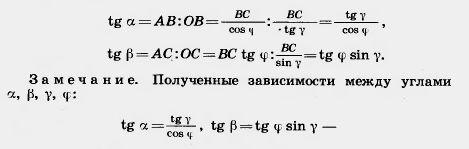 и ABC получаем:
и ABC получаем: 










 Урок математики "Двугранный угол. Многогранные углы" (0.18 MB)
Урок математики "Двугранный угол. Многогранные углы" (0.18 MB)
 1
1 3165
3165 706
706 Нравится
0
Нравится
0


