Презентация по геометрии "Призма"

ПРИЗМА

Автор: Крылова А.В.,

учитель математики

МБОУ «Видновская СОШ №2»

МО, г. Видное

2021

Понятие призмы

Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами. Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани — боковыми гранями призмы. В зависимости от основания призмы бывают: треугольными. четырёхугольными. шестиугольными и др.

Прямая призма

• Если боковые ребра перпендикулярны к основаниям, то призма называется прямой,

• Высота прямой призмы равна ее боковому ребру.

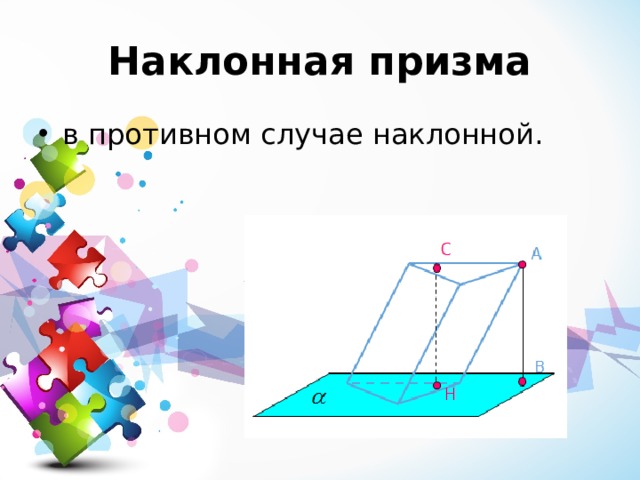
Наклонная призма

• в противном случае наклонной.

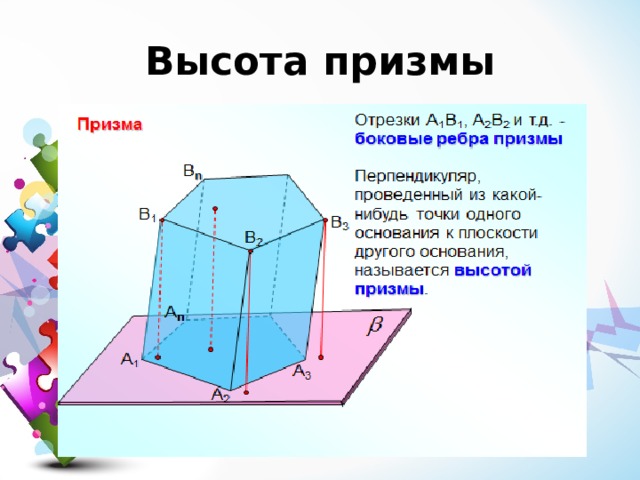
Высота призмы

• Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.

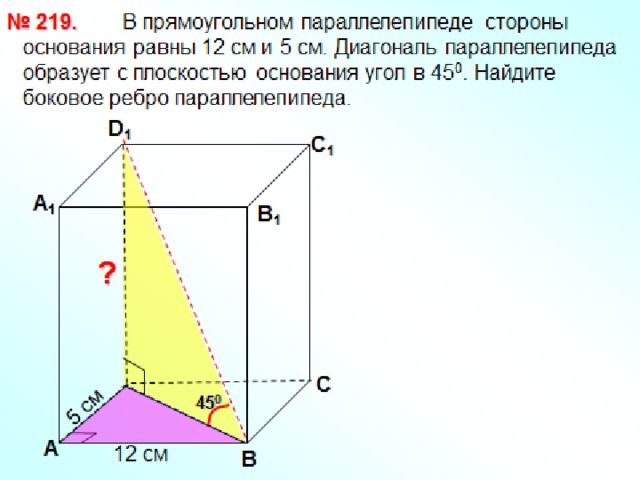
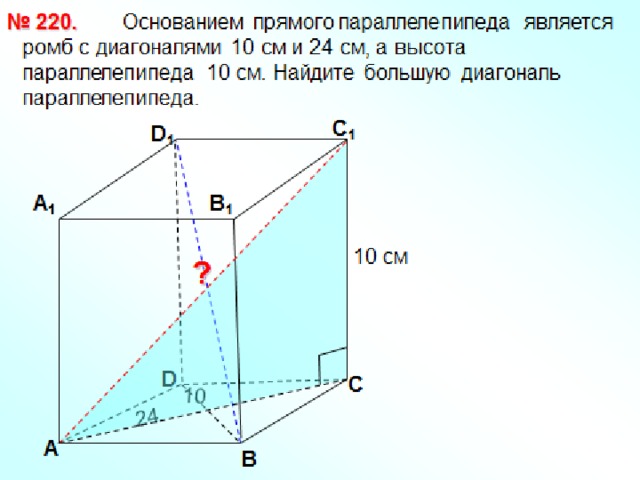
Задачи

• 1. Сторона основания правильной треугольной призмы равна 8 см, а диагональ боковой грани равна 10 см. Найдите площадь боковой и полной поверхности призмы.
• 2. Основание прямой призмы – параллелограмм со сторонами 8 и 15 см и углом 120о. Боковая поверхность призмы имеет площадь 460 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
• 3. Основание прямой призмы – прямоугольный треугольник с катетами 13 и 12 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

СПАСИБО ЗА ВНИМАНИЕ!