Презентация по алгебре по теме: «Примеры комбинаторных задач» в 9 классе

Элементы комбинаторики

Тема урока : «Примеры комбинаторных задач»

Тема урока: «Примеры комбинаторных вариантов»

9 класс ( 1 урок по теме)

Эпиграф урока:

«Число, место и комбинация –

три взаимно перекрещивающиеся,

но отличные сферы мышления, к которым можно отнести все математические идеи».

Дж. Сильвестр

.

.

Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из раздела множеств. Типичной задачей комбинаторики является задача перечисления комбинаций, составленных из нескольких предметов.

Из истории комбинаторики

С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.

Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности .

В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.

В Древней Греции

подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей и т.д .

Со временем появились различные игры (нарды, карты, шашки, шахматы и т. д.)

Леонард Эйлер(1707-1783)

Готфрид Вильгельм Лейбниц (1.07.1646 - 14.11.1716)

рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию , которая изучает общие свойства пространства и фигур.

Комбинаторику, как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г.

Он также впервые ввел термин «Комбинаторика».

Вывода формул, где использовал наиболее простые и наглядные методы, сопровождая их таблицами и примерами.

Его сочинения превзошло работы предшественников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью как научного трактата и как учебно-справочного издания.

Я. Бернулли

Методы решения комбинаторных задач

• Правило суммы.

2. Правило произведения

3. Таблицы.

4. Графы (деревья).

5. Формулы .

Вспомним несколько примеров таких задач

1. Несколько стран в качестве символа своего государства решили использовать флаг в виде 3-х горизонтальных полос одинаковых по ширине и цвету: синий, красный и белый. Сколько стран могут испытать такую символику при условии, что у каждой страны свой отличный от других флаг?

Будем искать решение с помощью Графа ( дерева) возможных вариантов .

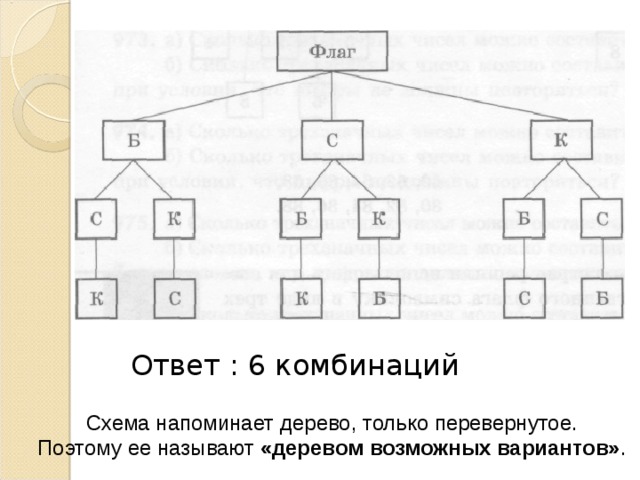
Ответ : 6 комбинаций

Схема напоминает дерево, только перевернутое.

Поэтому ее называют «деревом возможных вариантов» .

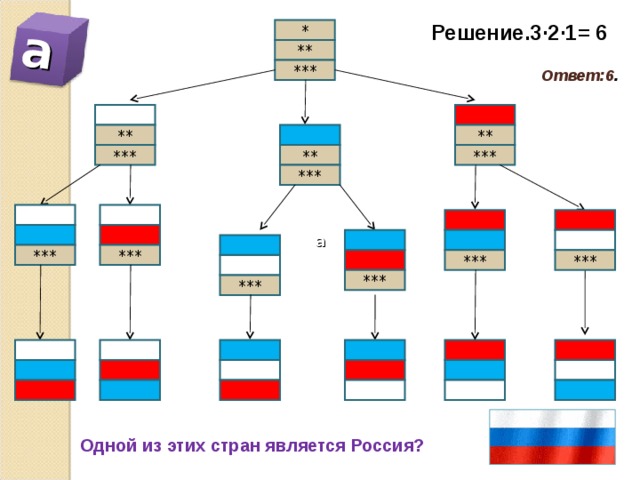
а

Решение.3·2·1= 6

*

**

Ответ:6 .

***

*

**

**

***

***

**

***

*

*

а

*

***

***

***

***

*

***

***

*

*

*

*

*

*

Одной из этих стран является Россия?

11

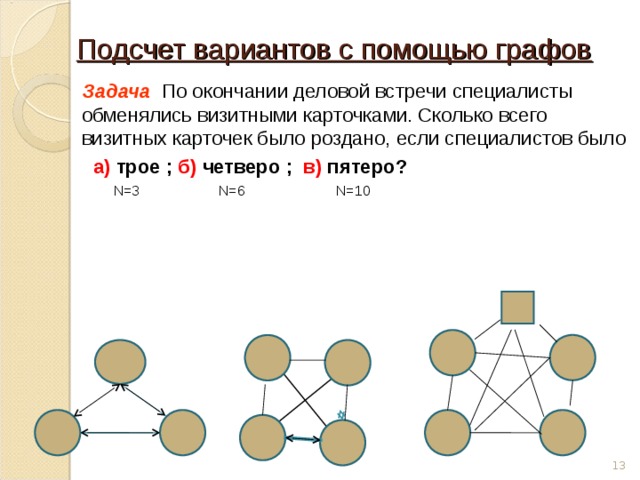
Подсчет вариантов с помощью графов

Задача По окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек было роздано, если специалистов было

а) трое ; б) четверо ; в) пятеро?

11

Подсчет вариантов с помощью графов

Задача По окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек было роздано, если специалистов было

а) трое ; б) четверо ; в) пятеро?

N=3 N=6 N=10

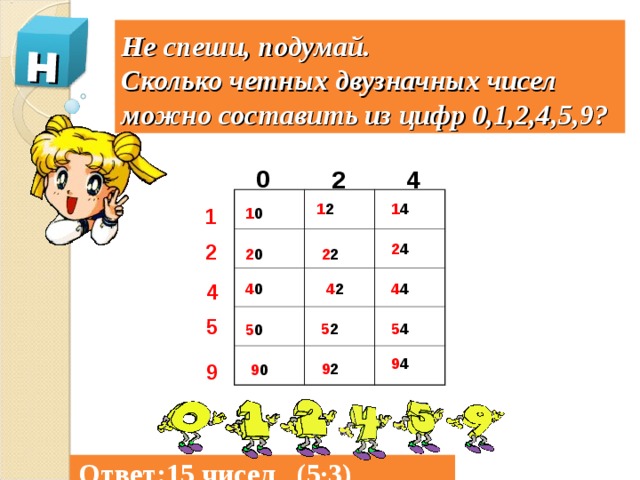
2. Сколько чётных двузначных чисел можно составить из цифр 0,1,2,4,5,9.  

н

Не спеши, подумай. Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?

0

4

2

1 2

1 4

1

1 0

2

2 4

2 0

2 2

4

4 4

4 2

4 0

5

5 2

5 4

5 0

9 4

9 2

9

9 0

Ответ:15 чисел (5·3)

15

3.На завтрак Валера может выбрать плюшку, бутерброд, пряник или кекс, а запить их может кофеем, соком или кефиром. Из скольких вариантов завтрака Валера может выбирать?

• Решим задачу, перебирая всевозможные варианты, путем кодирования вариантов завтрака

Решение: КП КБ К Пр КК

СП СБ С Пр СК

К-р П К-р Б К-р Пр К-р К

Ответ: 12 вариантов.

На завтрак Валера может выбрать: плюшку, бутерброд, пряник, или кекс, а запить он может: кофе, соком, кефиром. Сколько возможных вариантов завтрака?

м

Ответ:12 (4·3=12)

17

• Во всех задачах был осуществлён перебор всех возможных вариантов или комбинаций. Поэтому эти задачи называют комбинаторными. Слово комбинация происходит от латинского combino – соединяю.
• Действительно при получении любой комбинации мы составляем её из отдельных элементов последовательно соединяя их друг с другом. С этой точки зрения: число – это комбинация цифр, слово – это комбинация букв, меню – это комбинация блюд.
• Во всех предложенных задачах для подсчёта числа комбинаций мы использовали простой способ подсчёта – прямое перечисление (опираясь на «дерево возможных вариантов», таблицу, кодирование ). Но способ перебора возможных вариантов далеко не всегда применим, ведь количество комбинаций может исчисляться миллионами.
• Здесь на помощь приходят несколько замечательных комбинаторных правил, которые позволяют подсчитать количество комбинаций без их прямого перечисления. 

• Мы рассмотрели примеры 3-х разных задач, но получили совершенно одинаковые решения, которые основаны на общем

правиле умножения :

• Пусть имеется n элементов и требуется выбрать из них один за другим к элементов. Если первый элемент m 1 выбрать n 1 способами, после чего второй элемент m 2 выбрать n 2 способами из оставшихся, затем третий элемент m 3 выбрать n 3 способами из оставшихся и т.д., то число способов могут быть выбраны все к элементов, равно произведению

Примени это правило к каждой из решённых задач.

• 1-я задача: выбор верхней полосы - из 3-х цветов, т.е. n 1= 3; средняя полоса – из 2-х цветов, т.е. n 2 =2; нижняя полоса – из 1-го цвета, т.е. n 3 =1.

  n 1 n 2 n 3 = 3 * 2 * 1 = 6

• 2-я задача: заметим, что в этой задаче задействованы два независимых исхода, поэтому

m n = 5 *3 = 15

Решение задач в классе :

№ 714 .

• В кафе предлагают два первых блюда: борщ, рассольник — и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из первого и второго блюд, которые может заказать посетитель.

Проиллюстрируйте ответ, построив дерево возможных вариантов.

Решение.

Выберем одно блюдо ( борщ ) получим пары:

Б г; б к; б с; б п (4 пары).

• Теперь выберем рассольник :

Рг; р к; р с; р п (4 пары).

Согласно правилу комбинаторного умножения всего обедов: 2*4=8.

• Построив дерево возможностей, получим 8 вариантов.
• Ответ: б г; б к; б с; б п; р г; р к; р с; р п.; получим 8 разных обедов из двух блюд.

• № 716

Стадион имеет четыре входа: А, В, С и D . Укажите все возможные способы, какими посетитель может войти через один вход, а выйти через другой. Сколько таких способов?

Решение.

Из условия ясно, что порядок выбора имеет значение : АВ означает, что посетитель вошёл через А и вышел через В, а ВА означает, что вошёл через В, а вышел через А.

• первый вход, получаем 3 пары: АВ, АС, АД .
• второй вход : ВА, ВС, ВД .
• третий вход : СА, СВ, СД .
• четвёртый вход: ДА, ДВ, ДС .
• Общее количество способов выбора: 4*3=12 (к каждому из 4 входов мы дописывали 3 других).
• Замечание. По правилу произведения:
• первый выбор (через какой вход войти) можно сделать 4 способами (А, или В, или С, или Д);
• после этого второй выбор (через какой вход войти) можно сделать 3 способами ( любой вход, кроме того, через который вошли). Общее количество выбора равно 4*3=12.
• Ответ : 12 способов.
•  

• Решение.
• а) Выбираем поочерёдно:

16, 18, 61, 68, 81, 86.

• Всего 6 различных чисел

• № 721.

В шахматном турнире участвуют

9 человек. Каждый из них сыграл с каждым по одной партии. Сколько всего партий было сыграно?

• Решение.

Каждая пара играла между собой только один раз, порядок выбора не имеет значения (когда Иванов играл с Петровым, это то же самое, что Петров играл с Ивановым).

Выбрать первого участника партии можно 9 способами, а второго- 8 оставшимися способами;

по правилу произведения образуется 9*8=72 пары ,

но в это число каждая пара входит дважды: сначала Иванов-Петров, затем Петров- Иванов.

• Ответ : 36 партий.

19.04.19

а

А теперь поделись своим

настроением

• Дома :
• № 715,717,723,
• найти сообщение из истории комбинаторики

СПАСИБО ЗА УРОК

СПАСИБО ЗА УРОК

28